算額（その1189）

算額（その1189）

(12) 京都市伏見区御香宮門前町 御香宮神社（ごこうのみやじんじゃ）文久3年(1863)
近畿数学史学会：近畿の算額「数学の絵馬を訪ねて」，平成4年5月16日 初版第一刷，大阪教育図書株式会社，大阪市.
キーワード：円6個，直線上

直線上に互いに隣同士外接する甲，乙，丙，丁，戊の 5 個の円が載っており，それらの全てに外接する己円が載っている。甲，乙，丙円の直径がそれぞれ 4 寸，1.2 寸，1 寸のとき，戊円の直径はいかほどか。

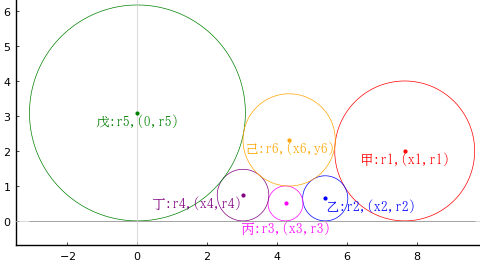
甲円の半径と中心座標を r1, (x1, r1)
乙円の半径と中心座標を r2, (x2, r2)
丙円の半径と中心座標を r3, (x3, r3)
丁円の半径と中心座標を r4, (x4, r4)
戊円の半径と中心座標を r5, (x5, y6)
己円の半径と中心座標を r6, (0, y6)
とおき，以下の連立方程式を解く。
なお，上の図は甲，乙，丙円の直径がそれぞれ 4 寸，1.29 寸，1 寸のときものである。乙円の直径が違うだけで，図は大きく変わる。与えられた条件のときの図は，後で掲示する。

include("julia-source.txt");

using SymPy
@syms r1::positive, x1::positive, r2::positive, x2::positive,
     r3::positive, x3::positive, r4::positive, x4::positive,
     r5::positive, r6::positive, x6::positive, y6::positive
#@syms r1, x1, r2, x2, r3, x3, r4, x4, r6, x6, y6, r5
#(r1, r2, r3) = (4//2, 12//20, 1//2)
eq1 = (x1 - x2)^2 + (r1 - r2)^2 - (r1 + r2)^2 |> expand
eq2 = (x1 - x6)^2 + (r1 - y6)^2 - (r1 + r6)^2 |> expand
eq3 = (x2 - x3)^2 + (r2 - r3)^2 - (r2 + r3)^2 |> expand
eq4 = (x2 - x6)^2 + (r2 - y6)^2 - (r2 + r6)^2 |> expand
eq5 = (x3 - x4)^2 + (r3 - r4)^2 - (r3 + r4)^2 |> expand
eq6 = (x3 - x6)^2 + (r3 - y6)^2 - (r3 + r6)^2 |> expand
eq7 = (x4 - x6)^2 + (r4 - y6)^2 - (r4 + r6)^2 |> expand
eq8 = x4^2 + (r4 - r5)^2 - (r4 + r5)^2 |> expand
eq9 = x6^2 + (y6 - r5)^2 - (r6 + r5)^2 |> expand;

using NLsolve

function nls(func, params...; ini = [0.0])
   if typeof(ini) <: Number
       r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params..., [ini]), ftol=big"1e-40")
       v = r.zero[1]
   else
       r = nlsolve((vout, vin)->vout .= func(vin, params...), ini, ftol=big"1e-40")
       v = r.zero
   end
   return Float64.(v), r.f_converged
end;

function H(u)
   (x1, x2, x3, r4, x4, r5, r6, x6, y6) = u
   return [
       -4*r1*r2 + x1^2 - 2*x1*x2 + x2^2,  # eq1
       -2*r1*r6 - 2*r1*y6 - r6^2 + x1^2 - 2*x1*x6 + x6^2 + y6^2,  # eq2
       -4*r2*r3 + x2^2 - 2*x2*x3 + x3^2,  # eq3
       -2*r2*r6 - 2*r2*y6 - r6^2 + x2^2 - 2*x2*x6 + x6^2 + y6^2,  # eq4
       -4*r3*r4 + x3^2 - 2*x3*x4 + x4^2,  # eq5
       -2*r3*r6 - 2*r3*y6 - r6^2 + x3^2 - 2*x3*x6 + x6^2 + y6^2,  # eq6
       -2*r4*r6 - 2*r4*y6 - r6^2 + x4^2 - 2*x4*x6 + x6^2 + y6^2,  # eq7
       -4*r4*r5 + x4^2,  # eq8
       -2*r5*r6 - 2*r5*y6 - r6^2 + x6^2 + y6^2,  # eq9
   ]
end;
(r1, r2, r3) = (4, 1.2, 1)./2
#(r1, r2, r3) = (4.0, 1.29, 1.0)./2
iniv = BigFloat[11.5, 9.3, 8.2, 0.94, 6.8, 12.5, 1, 8.5, 2]
res = nls(H, ini=iniv)

   ([11.502173707608492, 9.311283477587828, 8.215838362577495, 0.9375000000000001, 6.84653196881458, 12.500000000000012, 1.0125, 8.489699641330079, 1.9874999999999998], true)

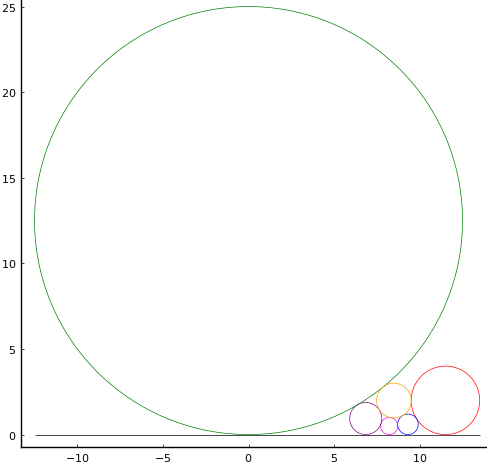
甲，乙，丙円の直径がそれぞれ 4 寸，1.2 寸，1 寸のとき，戊円の半径は 12.500000000000012 である（直径は 25 寸）。
このときの図は以下のようになる。

「術」でも，戊円の直径は 25 寸としており，間違いではない。

パラメータは以下のとおりである。

   r1 = 2;  x1 = 11.5022
   r2 = 0.6;  x2 = 9.31128
   r3 = 0.5;  x3 = 8.21584
   r4 = 0.9375;  x4 = 6.84653
   r5 = 12.5
   r6 = 1.0125;  x6 = 8.4897;  y6 = 1.9875

function draw(more)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (x1, x2, x3, r4, x4, r5, r6, x6, y6) = res[1]
   @printf("r1 = %g;  x1 = %g\n", r1, x1)
   @printf("r2 = %g;  x2 = %g\n", r2, x2)
   @printf("r3 = %g;  x3 = %g\n", r3, x3)
   @printf("r4 = %g;  x4 = %g\n", r4, x4)
   @printf("r5 = %g\n", r5)
   @printf("r6 = %g;  x6 = %g;  y6 = %g\n", r6, x6, y6)
   plot()
   circle(x1, r1, r1)
   circle(x2, r2, r2, :blue)
   circle(x3, r3, r3, :magenta)
   circle(x4, r4, r4, :purple)
   circle(0, r5, r5, :green)
   circle(x6, y6, r6, :orange)
   segment(-r5, 0, x1+r1, 0, :black)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(x1, r1, "甲:r1,(x1,r1)", :red, :center, delta=-delta/2)
       point(x2, r2, "乙:r2,(x2,r2)", :blue, :left, delta=-delta/2)
       point(x3, r3, "丙:r3,(x3,r3)", :magenta, :center, delta=-6delta)
       point(x4, r4, "丁:r4,(x4,r4)", :purple, :right, delta=-delta/2)
       point(0, r5, "戊:r5,(0,r5)", :green, :center, delta=-delta/2)
       point(x6, y6, "己:r6,(x6,y6)", :orange, :center, delta=-delta/2)
   end
end;

算額（その1188）

算額（その1188）

(10) 京都市中京区三条大宮西二筋目下ル 武信稲荷神社 嘉永6年(1853)
近畿数学史学会：近畿の算額「数学の絵馬を訪ねて」，平成4年5月16日 初版第一刷，大阪教育図書株式会社，大阪市.
キーワード：円5個，楕円

全円と楕円が交差しており，その隙間に等円が 4 個入っている。全円の直径が 10 寸のとき，等円の直径はいかほどか。

楕円の長半径，短半径，中心座標を a, b, (0, 0); a = R + 2r, b = R - 2r
全円の半径と中心座標を R, (0, 0)
等円の半径と中心座標を r, (a - r, 0), (0, b + r)
とする。
楕円に内接している円は一点で接している曲率円なので，半径は r = b^2/a である。

include("julia-source.txt");

using SymPy
@syms R::positive, r::positive, a::positive, b::positiv
a = R + 2r
b = R - 2r
eq = r - b^2/a
res = solve(eq, r)[1]
res |> println

   R*(5 - sqrt(17))/4

等円の半径 r は，全円の半径 R の (5 - √17)/4 倍である。
全円の直径が 10 寸のとき，等円の直径は 10*(5 - √17)/4 = 2.1922359359558485 寸である。

「術」は「5 から 17の平方根を引き，4 で割り，全円の直径を掛ける」と読めるので，上と同じ計算式である。
しかるに，「答」が 「2寸3分8厘4毛余り」となっている。

function draw(R, more)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r = R*(5 - sqrt(17))/4
   a = R + 2r
   b = R - 2r
   @printf("全円の直径が %g のとき，等円の直径は %g である。\n", 2R, 2r)
   plot()
   circle(0, 0, R)
   ellipse(0, 0, a, b, color=:green)
   circle2(a - r, 0, r, :blue)
   circle22(0, b + r, r, :blue)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(R + r, 0, "等円:r,(R+r,0) ", :blue, :right, :vcenter)
       point(0, R - r, "等円:r,(0,R-r)", :blue, :center, delta=-delta/2)
       point(a, 0, " a", :green, :left, :bottom, delta=delta)
       point(0, b, "b", :green, :center, delta=-delta)
       point(0, R, "R", :red, :center, :bottom, delta=delta)
   end
end;

draw(10/2, true)

算額（その1187）

算額（その1187）

(10) 京都市中京区三条大宮西二筋目下ル 武信稲荷神社 嘉永6年(1853)
近畿数学史学会：近畿の算額「数学の絵馬を訪ねて」，平成4年5月16日 初版第一刷，大阪教育図書株式会社，大阪市.
キーワード：円1個，直角三角形，正方形，斜線

直角三角形の中に，正方形と斜線で区切られた領域に全円を容れる。鈎，股が 21 寸，28 寸のとき，全円の直径はいかほどか。

鈎，股を「鈎」，「股」
正方形の一辺の長さを b，股上の正方形の頂点座標を (a, 0); b = 股 - a
全円の半径と中心座標を r, (a + r, b - r)
とおき，以下の連立方程式を解く。

include("julia-source.txt");

using SymPy
@syms 鈎::positive, 股::positive, a::positive, r::positiv
b = 股 - a
eq1 = (鈎 - b)/b - 鈎/股
eq2 = dist2(股, 鈎, a, 0, a + r, b - r, r)
res = solve([eq1, eq2], (r, a))[1]  # 1 of 2

   (股*鈎*(2*股 + 鈎 - sqrt(2*股^2 + 2*股*鈎 + 鈎^2))/(2*(股^2 + 2*股*鈎 + 鈎^2)), 股^2/(股 + 鈎))

鈎，股が 21 寸，28 寸のとき，全円の直径は 5.03612957434534 寸である。
ちなみに，正方形の一辺の長さは 12 寸である。

2res[1](鈎 => 21, 股 => 28).evalf() |> println
(股 - res[2])(鈎 => 21, 股 => 28).evalf() |> println

   5.03612957434534
   12.0000000000000

function draw(鈎, 股, more)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (r, a) = (股*鈎*(2*股 + 鈎 - sqrt(2*股^2 + 2*股*鈎 + 鈎^2))/(2*(股^2 + 2*股*鈎 + 鈎^2)), 股^2/(股 + 鈎))
   b = 股 - a
   @printf("鈎，股が %g, %g のとき，円の直径は %g である。\n", 鈎, 股, 2r)
   @printf("正方形の一辺の長さは %g である。\n", b)
   plot([0, 股, 股, 0], [0, 0, 鈎, 0], color=:green, lw=0.5)
   plot!([a, 股, 股, a, a], [0, 0, b, b, 0], color=:blue, lw=0.5)
   circle(a + r, b - r, r)
   segment(a, 0, 股, 鈎, :magenta)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(a, b, "(a,b) ", :blue, :right, :vcenter)
       point(a + r, b - r, "全円:r\n(a+r,b-r)", :red, :center, :bottom, delta=delta)
       point(股, 鈎, "(股,鈎) ", :green, :right, :vcenter)
   end
end;

draw(21, 28, true)

算額（その1186）

算額（その1186）

(10) 京都市中京区三条大宮西二筋目下ル 武信稲荷神社 嘉永6年(1853)
近畿数学史学会：近畿の算額「数学の絵馬を訪ねて」，平成4年5月16日 初版第一刷，大阪教育図書株式会社，大阪市.
キーワード：円4個，半円1個

半円と中円が交わってできる領域に等円 3 個を容れる。中円の直径が 1 寸のとき，等円の直径はいかほどか。

半円の半径と中心座標を R, (0, 0)
中円の半径と中心座標を r1, (0, r1)
等円の半径と中心座標を r2, (0, R + r2), (x2, r2)
とおき，以下の連立方程式を解く。

include("julia-source.txt");

using SymPy
@syms R::positive, r1::positive, r2::positive, x2::positiv
eq1 = R + 2r2 - 2r1
eq2 = x2^2 + (r1 - r2)^2 - (r1 + r2)^2
eq3 = x2^2 + r2^2 - (R - r2)^2
res = solve([eq1, eq2, eq3], (r2, x2, R))[2]  # 2 of 2

   (r1*(2 - sqrt(2))/2, r1*sqrt(4 - 2*sqrt(2)), sqrt(2)*r1)

等円の直径は中円の半径の (2 - √2)/2 倍である。
中円の直径が 1 寸のとき，等円の直径は (2 - √2)/2 = 0.2928932188134524 である。

その他のパラメータは以下の通りである。

  r1 = 0.5;  r2 = 0.146447;  x2 = 0.541196;  R = 0.707107

function draw(r1, more)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (r2, x2, R) = (r1*(2 - sqrt(2))/2, r1*sqrt(4 - 2*sqrt(2)), sqrt(2)*r1)
   @printf("中円の直径が %g のとき，等円の直径は %g である。\n", 2r1, 2r2)
   @printf("r1 = %g;  r2 = %g;  x2 = %g;  R = %g\n", r1, r2, x2, R)
   plot()
   circle(0, 0, R, beginangle=0, endangle=180)
   circle(0, r1, r1, :green)
   circle2(x2, r2, r2, :blue)
   circle(0, R + r2, r2, :blue)
   segment(-R, 0, R, 0, :red)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(R, 0, " R", :red, :left, :bottom, delta=delta/2)
       point(x2, r2, "等円:r2\n(x2,r2)", :blue, :center, delta=-delta)
       point(0, R + r2, "等円:r2\n(0,R+r2)", :blue, :center, delta=-delta)
       point(0, r1, "中円:r1,(0,r1)", :green, :center, delta=-delta)
   end
end;

draw(1/2, true)