算額(その78)
福島県船引町 蚕養国神社 明治24年(1891)2月
http://www.wasan.jp/fukusima/kogaikuni.html
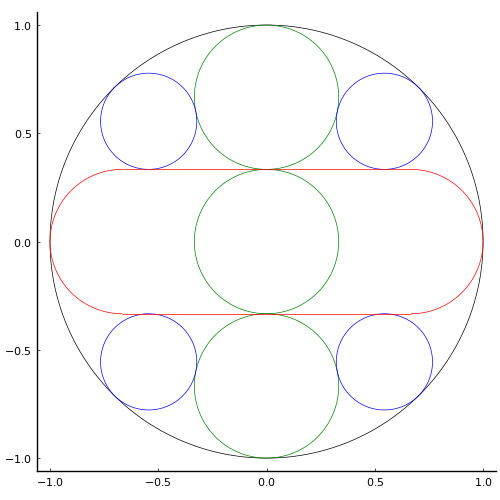
外円の中に 7 個の円が入っている。乙円の径が二寸のとき甲円の径はいくつか。

図のように記号を定め方程式を解く。
外円の半径を 1 とする。甲円の半径 r1 = 1/3,乙円の半径と中心座標を r2,(x2, r1+r2) とする。

using SymPy
@syms r1::positive, r2::positive, x2::positive;
r1 = 1//3
eq1 = x2^2 + (r1 - r2)^2 - (r1 + r2)^2
eq2 = x2^2 + (r1 + r2)^2 - (1 - r2)^2;
res = solve([eq1, eq2])
println(res)
Dict{Any, Any}[Dict(r2 => 2/9, x2 => 2*sqrt(6)/9)]
r1 = 1/3, r2 = 2/9 ゆえ,r1 = 3/2 * r2。算額は,「置く一個五分 乗乙径 甲径を得る」という。和算では「一個五分」とは 1.5 = 3/2 を表すのだなあ。
r2 = 2 寸ならば,r1 = 3 寸。
using Plots
function circle(ox, oy, r, color=:red; beginangle=0, endangle=360)
θ = beginangle:0.1:endangle
x = r.*cosd.(θ)
y = r.*sind.(θ)
plot!(ox .+ x, oy .+ y, color=color, linewidth=0.5)
end;
function point(x, y, string="", color=:green, position=:left, vertical=:top; fontsize=10, mark=true)
mark && scatter!([x], [y], color=color, markerstrokewidth=0)
annotate!(x, y, text(string, fontsize, vertical, position, color))
end;
function segment(x1, y1, x2, y2, color=:black; linestyle=:solid, linewidth=0.5)
plot!([x1, x2], [y1, y2], color=color, linestyle=linestyle, linewidth=linewidth)
end;
function draw(more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
(r1, r2, x2) = (1/3, 2/9, 2*sqrt(6)/9)
plot()
circle(0, 0, 1, :black)
circle(0, 0, r1, :green)
circle(0, 1-r1, r1, :green)
circle(0, r1-1, r1, :green)
circle(x2, r1+r2, r2, :blue)
circle(x2, -r1-r2, r2, :blue)
circle(-x2, r1+r2, r2, :blue)
circle(-x2, -r1-r2, r2, :blue)
circle(1-r1, 0, r1, beginangle=270, endangle=450)
circle(r1-1, 0, r1, beginangle= 90, endangle=270)
segment(r1-1, r1, 1-r1, r1, :red)
segment(r1-1, -r1, 1-r1, -r1, :red)
if more
println("甲円の径は $(3/2 * 2)")
point(0, 0, " O")
point(0, 1-r1, " 1-r1")
point(r1, 0, " r1")
point(x2, r1+r2, "(x2,r1+r2)", :magenta, :top)
hline!([0], color=:black, lw=0.5)
vline!([0], color=:black, lw=0.5)
end
end;
甲円の径は 3.0