算額(その67)
新潟県柏崎市 椎谷観音堂 寛政7年(1795)5月
http://www.wasan.jp/niigata/shiiyahukugen.png
長野県下高井郡 水穂神社 寛政12年正月
http://www.wasan.jp/nagano/mizuho1.html
外円の中に、5 本の斜線と甲円 1 個、乙円 5 個がある。甲円の径が 2889 寸であるとき、乙円の径を求めよ。
答えは 2584 寸
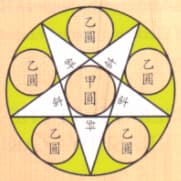
図のように記号を定め,方程式を解く。

using Plots
function circle(ox, oy, r, color=:red; beginangle=0, endangle=360)
θ = beginangle:0.1:endangle
x = r.*cosd.(θ)
y = r.*sind.(θ)
plot!(ox .+ x, oy .+ y, color=color, linewidth=0.5)
end;
function point0(x, y, string="", color=:green, position=:left, vertical=:top; mark=true)
mark && scatter!([x], [y], color=color, markerstrokewidth=0)
annotate!(x, y, text(string, 10, position, color, vertical))
end;
function distance(x1, y1, x2, y2, x0, y0)
p1, p2 = sympy.Point(x1, y1), sympy.Point(x2, y2)
l = sympy.Line(p1, p2)
l.distance(sympy.Point(x0, y0))
end;
function pentagon(x, y)
for i in 1:5
plot!([x[i], x[(i+2)%5+1]], [y[i], y[(i+2)%5+1]], color=:magenta, lw=0.5)
end
end
using SymPy
甲円,乙円の中心座標と線分 (x[2], y2]), (x[4], y[4]) の距離がそれぞれの円の半径である
function get_r1_r2(x, y) # 2 円の半径を求める
r1 = distance(x[2], y[2], x[4], y[4], 0, 0)
@syms r2::poitive
eq1 = distance(x[2], y[2], x[4], y[4], 0, 1-r2) - r2
res = solve(eq1)
return r1.evalf(), res[1].evalf()
end;
function draw(more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
plot()
point = -90:72:270
x = cosd.(point)
y = sind.(point)
pentagon(x, y)
r1, r2 = get_r1_r2(x, y)
println("r1 = $r1; r2 = $r2; 1-r2 = $(1-r2)")
circle(0, 0, 1)
circle(0, 0, r1)
for i = 90:72:378
circle((1-r2)*cosd(i), (1-r2)*sind(i), r2, :blue)
end
if more
point0(x[2], y[2], "(x[2],y[2])", :blue, :center)
point0(x[4], y[4], "(x[4],y[4]) ", :blue, :right)
point0(0, r1, "r1 ", :blue, :right)
point0(0, 0, "0 ", :blue, :right)
point0(0, 0, " 甲円", :blue)
point0(0, 1-r2, "1-r2 ", :blue, :right)
point0(0, 1-r2, " 乙圓", :blue,)
hline!([0], color=:black, lw=0.5)
vline!([0], color=:black, lw=0.5, xlims=(-1.15, 1.15))
end
end;
r1 = 0.309016994374948; r2 = 0.276393202250021; 1-r2 = 0.723606797749979
甲円の径が 2889 なら,乙円の径は 2584.0001547987517 となる。
r1 = 0.309016994374948; r2 = 0.276393202250021
2889/r1 * r2
2584.0001547987517



















