算額(その61)
長野市鬼無里 智光山文珠堂 明治11年(1878)8月
http://www.wasan.jp/nagano/monjudo1.html
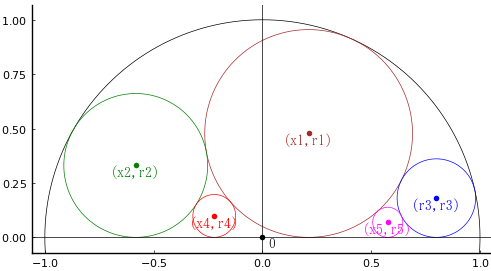
半円の中に 5 個の円がある。それぞれの径を求めよ。

半円の半径を 1 とし,図のように記号を定め,方程式を解く。
using SymPy
@syms x1::positive, r1::positive, x2::negative, r2::positive,
x3::positive, r3::positive, x4::negative, r4::positive,
x5::positive, r5::positive;
eq1 = x1^2 + r1^2 - (1 - r1)^2
eq2 = x3^2 + r3^2 - (1 - r3)^2
eq3 = x2^2 + r2^2 - (1 - r2)^2
eq4 = (x1 - x3)^2 + (r1 - r3)^2 - (r1 + r3)^2
eq5 = (x1 - x5)^2 + (r1 - r5)^2 - (r1 + r5)^2
eq6 = (x5 - x3)^2 + (r5 - r3)^2 - (r5 + r3)^2
eq7 = (x2 - x1)^2 + (r2 - r1)^2 - (r2 + r1)^2
eq8 = (x4 - x1)^2 + (r4 - r1)^2 - (r4 + r1)^2
eq9 = (x2 - x4)^2 + (r2 - r4)^2 - (r2 + r4)^2
eq10 = 1/r1 + 1/r3 + 2sqrt(1/r1/r3) - 1/r5; # デカルトの円定理
# res = solve([eq1, eq2, eq3, eq4, eq5, eq6, eq7, eq8, eq9, eq10])
この問題の場合も solve() では解けないので nlsolve() を用いる。
eq1 |> expand |> println
eq2 |> expand |> println
eq3 |> expand |> println
eq4 |> expand |> println
eq5 |> expand |> println
eq6 |> expand |> println
eq7 |> expand |> println
eq8 |> expand |> println
eq9 |> expand |> println
eq10 |> expand |> println
2*r1 + x1^2 - 1
2*r3 + x3^2 - 1
2*r2 + x2^2 - 1
-4*r1*r3 + x1^2 - 2*x1*x3 + x3^2
-4*r1*r5 + x1^2 - 2*x1*x5 + x5^2
-4*r3*r5 + x3^2 - 2*x3*x5 + x5^2
-4*r1*r2 + x1^2 - 2*x1*x2 + x2^2
-4*r1*r4 + x1^2 - 2*x1*x4 + x4^2
-4*r2*r4 + x2^2 - 2*x2*x4 + x4^2
-1/r5 + 1/r3 + 1/r1 + 2/(sqrt(r1)*sqrt(r3))
using NLsolve
function nls(func, params...; ini = [0.0])
if typeof(ini) <: Number
r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params...), [ini], ftol=1e-14)
v = r.zero[1]
else
r = nlsolve((vout, vin)->vout .= func(vin, params...), ini, ftol=1e-14)
v = r.zero
end
return v, r.f_converged
end;
function H(u)
x1, r1, x2, r2, x3, r3, x4, r4, x5, r5 = u
return [
2*r1 + x1^2 - 1
2*r3 + x3^2 - 1
2*r2 + x2^2 - 1
-4*r1*r3 + x1^2 - 2*x1*x3 + x3^2
-4*r1*r5 + x1^2 - 2*x1*x5 + x5^2
-4*r3*r5 + x3^2 - 2*x3*x5 + x5^2
-4*r1*r2 + x1^2 - 2*x1*x2 + x2^2
-4*r1*r4 + x1^2 - 2*x1*x4 + x4^2
-4*r2*r4 + x2^2 - 2*x2*x4 + x4^2
-1/r5 + 1/r3 + 1/r1 + 2/(sqrt(r1)*sqrt(r3))
];
end;
iniv = [0.01, 0.5, -0.7, 0.22, 0.8, 0.19, -0.5, 0.05, 0.4, 0.05];
res = nls(H, ini=iniv)
([0.21236918980148334, 0.47744966361153107, -0.5821590777643445, 0.3305454040882841, 0.7994277491932246, 0.18045763690992736, -0.22131238148404836, 0.0984814314508113, 0.5759211572513911, 0.06920626565999469], true)

using Plots
function circle(ox, oy, r, color=:red; beginangle=0, endangle=360)
θ = beginangle:0.1:endangle
x = r.*cosd.(θ)
y = r.*sind.(θ)
plot!(ox .+ x, oy .+ y, color=color, linewidth=0.5)
end;
function point(x, y, string="", color=:green, position=:left, vertical=:top; mark=true)
mark && scatter!([x], [y], color=color, markerstrokewidth=0)
annotate!(x, y, text(string, 10, position, color, vertical))
end;
function draw(more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
plot(ylims=(-0.07, 1.07))
x1, r1, x2, r2, x3, r3, x4, r4, x5, r5 = [0.21236918980148334, 0.47744966361153107, -0.5821590777643445, 0.3305454040882841, 0.7994277491932246, 0.18045763690992736, -0.22131238148404836, 0.0984814314508113, 0.5759211572513911, 0.06920626565999469]
println("x1 = $x1, r1 = $r1\nx2 = $x2, r2 = $r2\nx3 = $x3, r3 = $r3\nx4 = $x4, r4 = $r4\nx5 = $x5, r5 = $r5")
circle(0, 0, 1, :black)
circle(x1, r1, r1, :brown)
circle(x2, r2, r2, :green)
circle(x3, r3, r3, :blue)
circle(x4, r4, r4, :red)
circle(x5, r5, r5, :magenta)
hline!([0], color=:black, lw=0.5)
if more
point(0, 0, " 0", :black)
point(x1, r1, "(x1,r1)", :brown, :center)
point(x2, r2, "(x2,r2)", :green, :center)
point(x3, r3, "(r3,r3)", :blue, :center)
point(x4, r4, "(x4,r4)", :red, :center)
point(x5, r5, "(x5,r5)", :magenta, :center)
vline!([0], color=:black, lw=0.5)
end
end;
x1 = 0.21236918980148334, r1 = 0.47744966361153107
x2 = -0.5821590777643445, r2 = 0.3305454040882841
x3 = 0.7994277491932246, r3 = 0.18045763690992736
x4 = -0.22131238148404836, r4 = 0.0984814314508113
x5 = 0.5759211572513911, r5 = 0.06920626565999469

































