算額(その72)
四二 浦和市西堀(現さいたま市桜区西堀) 氷川神社 嘉永5年(1852)
埼玉県立図書館:埼玉県史料集 第二集『埼玉の算額』,昭和44年,誠美堂印刷所,埼玉県与野市.
埼玉県浦和市西堀 氷川神社 嘉永5年
http://www.wasan.jp/saitama/uhikawa.html
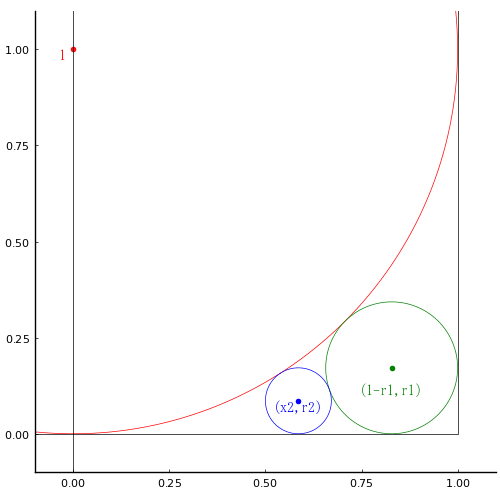
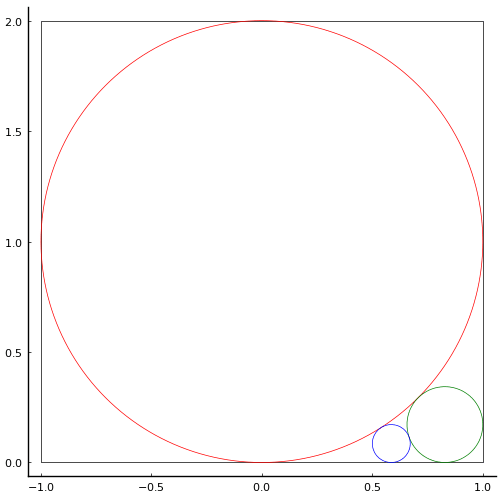
正方形の中に大円,中円,小円が互いに接して入っている。中円の径が 10 寸のとき,小円の径はいかほどか。
下図のように,大円,中円,小円の半径と中心座標をそれぞれ {1, (0, 1)}, {r1, (1-r1, r1)}, {r2,(x2, r2)} とし,方程式を立てて解く。
using SymPy
@syms r1::positive, x2::positive, r2::positive
eq1 = (1 - r1)^2 + (1 - r1)^2 - (1 + r1)^2;
eq2 = x2^2 + (1 - r2)^2 - (1 + r2)^2;
eq3 = (1 - r1 - x2)^2 + (r1 - r2)^2 - (r1 + r2)^2;
results = solve([eq1, eq2, eq3], (r1, r2, x2));
results[2]
(3 - 2*sqrt(2), 3/2 - sqrt(2), 2 - sqrt(2))
小円の径は中円の径の r2/r1
(3/2 - sqrt(2)) / (3 - 2*sqrt(2)) # r2/r1
0.5
よって、中円の径が 10 寸ならば、小円の径は 5 寸である。
using Plots
function circle(ox, oy, r, color=:red; beginangle=0, endangle=360)
θ = beginangle:0.1:endangle
x = r.*cosd.(θ)
y = r.*sind.(θ)
plot!(ox .+ x, oy .+ y, color=color, linewidth=0.5)
end;
function point(x, y, string="", color=:green, position=:left, vertical=:top; fontsize=10, mark=true)
mark && scatter!([x], [y], color=color, markerstrokewidth=0)
annotate!(x, y, text(string, fontsize, position, color, vertical))
end;
function segment(x1, y1, x2, y2, color=:black; linestyle=:solid, linewidth=0.5)
plot!([x1, x2], [y1, y2], color=color, linestyle=linestyle, linewidth=linewidth)
end;
function draw(more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="")#, fontfamily="IPAMincho")
(r1, r2, x2) = (3 - 2*sqrt(2), 3/2 - sqrt(2), 2 - sqrt(2))
plot([-1, 1, 1, -1, -1], [0, 0, 2, 2, 0], color=:black, lw=0.5)
circle(0, 1, 1)
circle(1 - r1, r1, r1, :green)
circle(x2, r2, r2, :blue)
if more
println("r1 = $r1")
println("r2 = $r2")
println("x2 = $x2)")
println("r2/r1 = $(r2/r1)")
point(0, 1, "1 ", :red, :right)
point(1 - r1, r1, "\n(1-r1,r1)", :green, :center)
point(x2, r2, "(x2,r2)", :blue, :center)
vline!([0], color=:black, lw=0.5, xlims=(-0.1, 1.1), ylims=(-0.1, 1.1))
end
end;
r1 = 0.1715728752538097
r2 = 0.08578643762690485
x2 = 0.5857864376269049)
r2/r1 = 0.5


















