算額（その49）

算額（その49）

岩手県東磐井郡川崎村 鳥森神社
現在は一関市のようだが，鳥森神社は見当たらない（烏森神社でもない）http://www.wasan.jp/iwate/torimori.html

外円の中に 3 種類の円が 2 つずつ入っている。それぞれの径を求めよ。

以下のように記号を定め，方程式を解く。

using SymPy
@syms r1::positive, r2::positive, r3::positive;

eq1 = (1 - r2)^2 + (1 - r3)^2 - (r2 + r3)^2 |> expand  # 甲円と乙円が外接する
eq1 |> println

   -2*r2*r3 - 2*r2 - 2*r3 + 2

eq2 = r1^2 + (1 - r3)^2 - (r1 + r3)^2 |>expand  # 甲円と丙円が外接する
eq2 |> println

   -2*r1*r3 - 2*r3 + 1

eq3 = 2(r1 + r2) - 1 |> expand  # 乙円と丙円の直径の和が外円の半径である
eq3 |> println

   2*r1 + 2*r2 - 1

res = solve([eq1, eq2, eq3], (r1, r2, r3))

   1-element Vector{Tuple{Sym, Sym, Sym}}:
    (-1 + sqrt(5)/2, 3/2 - sqrt(5)/2, sqrt(5)/5)

using Plots

function circle(ox, oy, r, color=:red; beginangle=0, endangle=360)
   θ = beginangle:0.1:endangle
   x = r.*cosd.(θ)
   y = r.*sind.(θ)
   plot!(ox .+ x, oy .+ y, color=color, linewidth=0.5)
end;

function point(x, y, string="", color=:green, position=:left, vertical=:top; mark=true)
   mark && scatter!([x], [y], color=color, markerstrokewidth=0)
   annotate!(x, y, text(string, 10, position, color, vertical))
end;

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   plot()
   (r1, r2, r3) = (-1 + sqrt(5)/2, 3/2 - sqrt(5)/2, sqrt(5)/5)
   println("r1 = $r1;  r2 = $r2;  r3 = $r3")
   circle(0, 0, 1, :black)
   circle(r1, 0, r1)
   circle(-r1, 0, r1)
   circle(1-r2, 0, r2, :blue)
   circle(-1+r2, 0, r2, :blue)
   circle(0, 1-r3, r3, :green)
   circle(0, -1+r3, r3, :green)
   if more
       point(r1, 0, " r1", :red, :left)
       point(1-r2, 0, " 1-r2", :blue, :left)
       point(0, 1-r3, " 1-r3", :green, :left)
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5)
   end
end;

   r1 = 0.1180339887498949;  r2 = 0.3819660112501051;  r3 = 0.447213595499958

 

算額（その48）

算額（その48）

山形県鶴岡市羽黒町 出羽三山神社
http://www.wasan.jp/yamagata/haguro.html
http://www.wasan.jp/yamagata/haguro3.png

以下のように記号を定め方程式を解く。

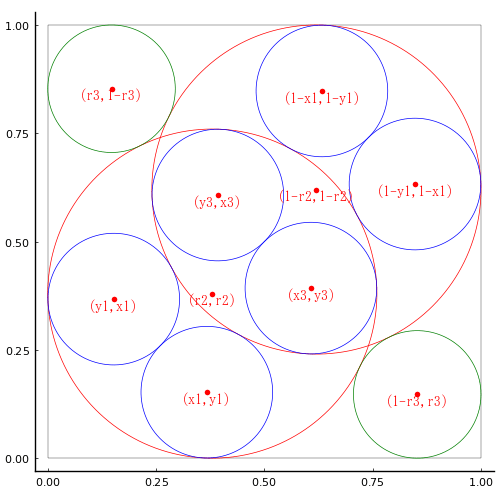
using SymPy
@syms r1::positive, r2::positive, r3::positive;
@syms x1::positive, y1::positive;

eq0 = 2(x1 - y1)^2 - 4r1^2 |> expand  # 左下の 2 円が外接する
eq0 |> println

   -4*r1^2 + 2*x1^2 - 4*x1*y1 + 2*y1^2

x3 = 1//2 + r1/sqrt(Sym(2));  # 中央の 2 円の中心は (1/2, 1/2) からわかる
y3 = 1//2 - r1/sqrt(Sym(2));
(x3, y3) |> println

   (sqrt(2)*r1/2 + 1/2, -sqrt(2)*r1/2 + 1/2)

eq1 = (1 - r3 - r2)^2 +(r2 - r3)^2 - (r2 + r3)^2 |>expand  # 左下大円と右下小円が外接する
eq1 |> println

   r2^2 - 2*r2*r3 - 2*r2 + r3^2 - 2*r3 + 1

eq2 = (x1 - (1 - r2))^2 + (y1 - (1 - r2))^2 - (r1 + r2)^2 |> expand  # 右上大円と左下小円が外接する
eq2 |> println

   -r1^2 - 2*r1*r2 + r2^2 + 2*r2*x1 + 2*r2*y1 - 4*r2 + x1^2 - 2*x1 + y1^2 - 2*y1 + 2

eq4 = (r2 - x1)^2 + (r2 - y1)^2 - (r2 - r1)^2 |> expand  # 左下大円と左下小円が内接する
eq4 |> println

   -r1^2 + 2*r1*r2 + r2^2 - 2*r2*x1 - 2*r2*y1 + x1^2 + y1^2

eq5 = (1 - r2 - x3)^2 + (1 - r2 - y3)^2 - (r2 - r1)^2 |> expand  # 右上大円と中央下の小円が内接する
eq5 |> println

   2*r1*r2 + r2^2 - 2*r2 + 1/2

未知数は r1, r2, r3, x1, y1 の 5 個，方程式は 5 本。これで解ける。

res = solve([eq0, eq1, eq2, eq4, eq5], (r1, r2, r3, x1, y1));

8 組の解が得られるが 2 番目と 4 番目が適切な解である。2 番目と 4 番目の違いは x1, y1 が入れ替わっているだけ。図では x1 > y1 なので 4 番目の解を示しておく。

res[4] |> println

   (2/9 - sqrt(10)/45, (-4207*sqrt(10)/18 - 220*sqrt(55 - 10*sqrt(10))/3 + 805*sqrt(22 - 4*sqrt(10))/6 + 7175/9)/(-308*sqrt(10) - 93*sqrt(5)*sqrt(11 - 2*sqrt(10)) + 195*sqrt(2)*sqrt(11 - 2*sqrt(10)) + 1127), 2*sqrt(-4207*sqrt(10) - 1320*sqrt(5)*sqrt(11 - 2*sqrt(10)) + 2415*sqrt(2)*sqrt(11 - 2*sqrt(10)) + 14350)/(3*(-33 - 5*sqrt(2)*sqrt(11 - 2*sqrt(10)) + sqrt(5)*sqrt(11 - 2*sqrt(10)) + 6*sqrt(10))) + (-67*sqrt(10)/6 - 19*sqrt(55 - 10*sqrt(10))/9 + 145*sqrt(22 - 4*sqrt(10))/18 + 164/3)/(-6*sqrt(10) - sqrt(5)*sqrt(11 - 2*sqrt(10)) + 5*sqrt(2)*sqrt(11 - 2*sqrt(10)) + 33), -sqrt(10)/9 + sqrt(55 - 10*sqrt(10))/45 + 11/18, -sqrt(10)/9 - sqrt(11/405 - 2*sqrt(10)/405) + 11/18)

res[4][1] |> simplify |> println  # r1

   2/9 - sqrt(10)/45

res[4][2] |> simplify |> println  # r2

   (-4207*sqrt(10)/18 - 220*sqrt(55 - 10*sqrt(10))/3 + 805*sqrt(22 - 4*sqrt(10))/6 + 7175/9)/(-308*sqrt(10) - 93*sqrt(5)*sqrt(11 - 2*sqrt(10)) + 195*sqrt(2)*sqrt(11 - 2*sqrt(10)) + 1127)

res[4][3] |> simplify |> println  # r3

   ((-396 - 60*sqrt(22 - 4*sqrt(10)) + 12*sqrt(55 - 10*sqrt(10)) + 72*sqrt(10))*sqrt(-4207*sqrt(10) - 1320*sqrt(5)*sqrt(11 - 2*sqrt(10)) + 2415*sqrt(2)*sqrt(11 - 2*sqrt(10)) + 14350)/18 + (-201*sqrt(10) - 38*sqrt(55 - 10*sqrt(10)) + 145*sqrt(22 - 4*sqrt(10)) + 984)*(-6*sqrt(10) - sqrt(55 - 10*sqrt(10)) + 5*sqrt(22 - 4*sqrt(10)) + 33)/18)/(-6*sqrt(10) - sqrt(5)*sqrt(11 - 2*sqrt(10)) + 5*sqrt(2)*sqrt(11 - 2*sqrt(10)) + 33)^2

res[4][4] |> simplify |> println  # x1

   -sqrt(10)/9 + sqrt(55 - 10*sqrt(10))/45 + 11/18

res[4][5] |> simplify |> println  # y1

   -sqrt(10)/9 - sqrt(55 - 10*sqrt(10))/45 + 11/18

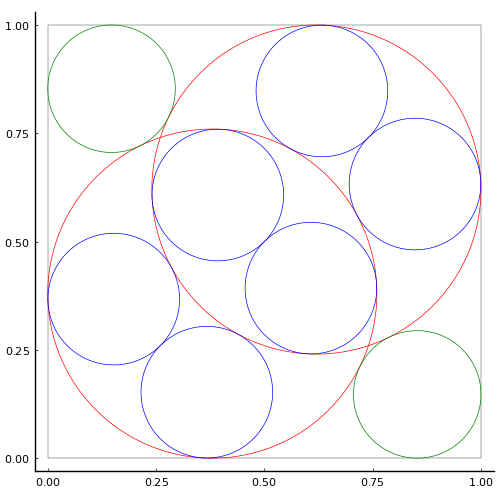
using Plots

function circle(ox, oy, r, color=:red; beginangle=0, endangle=360)
   θ = beginangle:0.1:endangle
   x = r.*cosd.(θ)
   y = r.*sind.(θ)
   plot!(ox .+ x, oy .+ y, color=color, linewidth=0.5)
end;

function point(x, y, string="", color=:green, position=:left, vertical=:top; mark=true)
   mark && scatter!([x], [y], color=color, markerstrokewidth=0)
   annotate!(x, y, text(string, 10, position, color, vertical))
end;

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   plot([0, 1, 1, 0, 0], [0, 0, 1, 1, 0], color=:black, linewidth=0.25)
   (r1, r2, r3, x1, y1) = # (2/9 - sqrt(10)/45, (-4207*sqrt(10)/18 - 805*sqrt(22 - 4*sqrt(10))/6 + 220*sqrt(55 - 10*sqrt(10))/3 + 7175/9)/(-308*sqrt(10) - 195*sqrt(2)*sqrt(11 - 2*sqrt(10)) + 93*sqrt(5)*sqrt(11 - 2*sqrt(10)) + 1127), 2*sqrt(-4207*sqrt(10) - 2415*sqrt(2)*sqrt(11 - 2*sqrt(10)) + 1320*sqrt(5)*sqrt(11 - 2*sqrt(10)) + 14350)/(3*(-33 - sqrt(5)*sqrt(11 - 2*sqrt(10)) + 5*sqrt(2)*sqrt(11 - 2*sqrt(10)) + 6*sqrt(10))) + (-67*sqrt(10)/6 - 145*sqrt(22 - 4*sqrt(10))/18 + 19*sqrt(55 - 10*sqrt(10))/9 + 164/3)/(-6*sqrt(10) - 5*sqrt(2)*sqrt(11 - 2*sqrt(10)) + sqrt(5)*sqrt(11 - 2*sqrt(10)) + 33), -sqrt(10)/9 - sqrt(55 - 10*sqrt(10))/45 + 11/18, -sqrt(10)/9 + sqrt(11/405 - 2*sqrt(10)/405) + 11/18)
                            (2/9 - sqrt(10)/45, (-4207*sqrt(10)/18 - 220*sqrt(55 - 10*sqrt(10))/3 + 805*sqrt(22 - 4*sqrt(10))/6 + 7175/9)/(-308*sqrt(10) - 93*sqrt(5)*sqrt(11 - 2*sqrt(10)) + 195*sqrt(2)*sqrt(11 - 2*sqrt(10)) + 1127), 2*sqrt(-4207*sqrt(10) - 1320*sqrt(5)*sqrt(11 - 2*sqrt(10)) + 2415*sqrt(2)*sqrt(11 - 2*sqrt(10)) + 14350)/(3*(-33 - 5*sqrt(2)*sqrt(11 - 2*sqrt(10)) + sqrt(5)*sqrt(11 - 2*sqrt(10)) + 6*sqrt(10))) + (-67*sqrt(10)/6 - 19*sqrt(55 - 10*sqrt(10))/9 + 145*sqrt(22 - 4*sqrt(10))/18 + 164/3)/(-6*sqrt(10) - sqrt(5)*sqrt(11 - 2*sqrt(10)) + 5*sqrt(2)*sqrt(11 - 2*sqrt(10)) + 33), -sqrt(10)/9 + sqrt(55 - 10*sqrt(10))/45 + 11/18, -sqrt(10)/9 - sqrt(11/405 - 2*sqrt(10)/405) + 11/18)
   x3, y3 = (sqrt(2)*r1/2 + 1/2, -sqrt(2)*r1/2 + 1/2)
   println("r1 = $r1;  r2 = $r2;  r3 = $r3")
   println("x1 = $x1;  y1 = $y1;  x3 = $x3;  y3 = $y3")
   x5 = r2
   y5 = r2
   circle(x5, y5, r2)
   x8 = 1-r2
   y8 = 1-r2
   circle(x8, y8, r2)
   circle(x1, y1, r1, :blue)
   x2 = y1
   y2 = x1
   circle(x2, y2, r1, :blue)
   x4 = y3
   y4 = x3
   circle(x3, y3, r1, :blue)
   circle(x4, y4, r1, :blue)
   x6 = 1 - x2
   y6 = 1 - y2
   circle(x6, y6, r1, :blue)
   x7 = 1 - x1
   y7 = 1 - y1
   circle(x7, y7, r1, :blue)
   x9 = 1 - r3
   y9 = r3
   circle(x9, y9, r3, :green)
   x10 = y9
   y10 = x9
   circle(x10, y10, r3, :green)
   if more
       point(x1, y1, "(x1,y1)", :red, :center)
       point(x2, y2, "(y1,x1)", :red, :center)
       point(x3, y3, "(x3,y3)", :red, :center)
       point(x4, y4, "(y3,x3)", :red, :center)
       point(x5, y5, "(r2,r2)", :red, :center)
       point(x6, y6, "(1-y1,1-x1)", :red, :center)
       point(x7, y7, "(1-x1,1-y1)", :red, :center)
       point(x8, y8, "(1-r2,1-r2)", :red, :center)
       point(x9, y9, "(1-r3,r3)", :red, :center)
       point(x10, y10, "(r3,1-r3)", :red, :center)
   end
end;

   r1 = 0.15194938532959157;  r2 = 0.3798734633239779;  r3 = 0.14719594941536762
   x1 = 0.3671913674116398;  y1 = 0.15230248588427597;  x3 = 0.6074444407636819;  y3 = 0.3925555592363181