2乗の数を出すための 第三 の計算法 ということで話を進めます。
まだ、あるんですか、という感じですが、実際自分が暗算するときに無意識にやっていた方法があって、
それも実際捨てがたたく、ご紹介したくなった次第です。
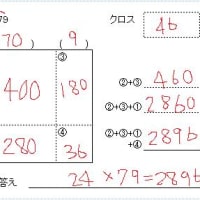
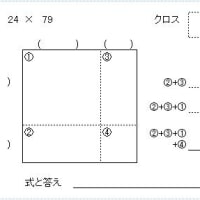
その方法ですが、例えば 79 の2乗を考える際に、例のごとく「4つの四角形」をつかって考えます。
その時、少し工夫をして 80 の2乗から入るのですね。
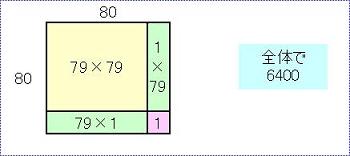
上図の様に、全体は 80×80 で 6400 なんですが、79×79 と
それ以外のところに分解、79×79 以外の部分を取り去ってしまえば、答えが出ます、という発想なんです。
しかしその時に、ご丁寧に
79×1 の部分を引いて、
1×79の部分を引いて、
1×1 の部分を引いて、
はい、答えです、という手順を踏むのではなく、
80を2回引いてしまえ、そのあと、引きすぎた 1 を戻そう
という計算をするのです。
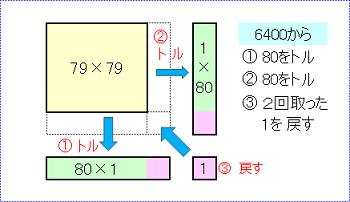
計算式にすれば、
79×79 = 80×80 - 80 - 80 + 1
= 6400 - 160 + 1
= 6241
となります。
80を2回引く、というのは 頭の中のイメージ であって、もちろん計算上は、
79×79 = 80×80 - 80 × 2 + 1
= 6400 - 160 + 1
= 6241
これで、良いと思います。
但し、私の場合は、この計算をするときに上記のような図を頭の中に強烈にイメージし、
実際に 下側、右側、これを「トル」、そしてカドのコマを「戻す」ということをやっているので、
どうしても「80を2回引く」という発想になってしまいます。
もっとスマートに計算出来る方なら、初めから「80×2」でいいと思います。
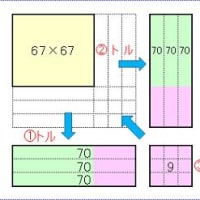
他の例を見ます: 67×67
もちろん、四角形としては 70×70 を考えます。
但し、前回の場合と違い、70 と 67 の差は 3 あります。

そこで、私のイメージの中では、上記の様ように、67×1 が 縦横 3本ずつ、計六本 出てきます。
右下の「コマ」の中には点線が入っていて、9コマに分かれているというイメージです。
そして、これを70として 6本分、4900 から取っ払う、という感じです。
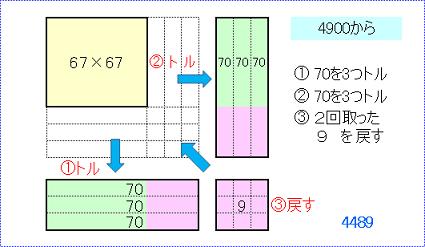
最後に 9 を戻して計算終了、ということですが、もちろん式としては
67×67 = 70 × 70 - 70 × 6 + 9
= 4900 - 420 + 9
= 4480 + 9
= 4489
となります。
慣れてくれば、四角をイメージしつつも一発で、
67×67 = 4900 - 420 + 9
= 4489
と計算できるようになると思います。
なんだ、最初に紹介した4角形の計算方法と大して変わらないじゃないか、と思われるかも知れませんが、
それほど、4角形をイメージするという手法は、基本であり、応用が効くのだと思います。
以上、例を見た数字は、下一桁が9、7、と10に近い数でした。
もちろん、これが逆に0に近ければ、

より大きな数を考えて、トル、というのではなく、
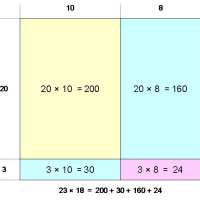
順当に10の位 と 1の位 で分けた4角形を考えて積み上げるということで良いと思います。
(この場合は、私は 10×3 のイメージでOKなんです )
)
ただ、ここでもう一つ計算例を出したいと思います。
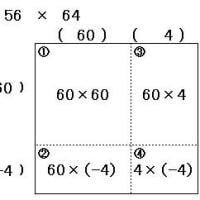
例えば 36×36 これを (35+1)×(35+1)と考えます。

そこで、35×35 の部分は 速算が効いて 1225 とすぐに判りますから、これを使おうという発想です。
36×36 = 35×35 + 35×2 + 1
= 1225 + 70 + 1
= 1295 + 1
= 1296
これを (30+6)×(30+6)として計算すると、
36×36 = 30×30 + 180×2 + 36
= 900 + 360 + 36
= 1260 + 36
= 1296
となりますね。出来ないこともないですが、前者と比べるとやや忙しいでしょうか。
同様に、34×34なら、35×35を使って、
36×36 = 35×35 - 35×2 + 1
= 1225 - 70 + 1
= 1155 + 1
= 1156
と計算出来ます。これは例としてあげました。

色々な計算方法をあげています。もちろん、どの計算方法が一番良いのか、ということはないと思います。
一つの計算を様々な方法で行うこと自体、面白いな、と感じますし、
新たな見かたをすることによって、違った発見があることがあります。
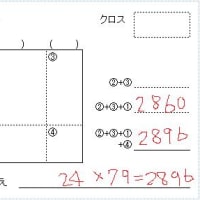
例えば、今回紹介した計算方法により 27×27 を計算します。
まず 30 という数字を考え、30×30 を踏まえて、
900 から 30 を 6 回引く これに 9 を足す、だな、という形になります。
すると、900-30×6 つまり 900-180=720、プラス 9 となります。
こういう風に入って行くと、27×27=729 という暗記も何となくスムースに行きませんでしょうか。
何か、100の位の10の位の 72 というのが何か必然的に見えてきました。
そもそも 27 は 9 の倍数なので、27 の 2乗 も 9 の倍数であり、下一桁が 9 なので、
残りの720の部分も 9 の倍数、ということもありましょうが、
何と、900-180 という求め方がある、と考えたら、覚えやすいですよね。
こういう風にああでもない、こうでもないと考えていると、27の2乗は、729 以外にあり得ない、
そう思えてきます。
そんなこと言ったら、どんな数だって2乗の数は決まっていて、それ以外にあり得ないのですが、ともかくも、
そういう風に思えてくるということです。
次回にこの計算方法を用いた暗記リストを提示します。
数字の動きを見ることによって、上記の 27 の例の様に、何か引っかかる部分が出てくると思います。
それが以外に暗記の役にたつのでは、と考えます。


まだ、あるんですか、という感じですが、実際自分が暗算するときに無意識にやっていた方法があって、
それも実際捨てがたたく、ご紹介したくなった次第です。
その方法ですが、例えば 79 の2乗を考える際に、例のごとく「4つの四角形」をつかって考えます。
その時、少し工夫をして 80 の2乗から入るのですね。

上図の様に、全体は 80×80 で 6400 なんですが、79×79 と
それ以外のところに分解、79×79 以外の部分を取り去ってしまえば、答えが出ます、という発想なんです。
しかしその時に、ご丁寧に
79×1 の部分を引いて、
1×79の部分を引いて、
1×1 の部分を引いて、
はい、答えです、という手順を踏むのではなく、
80を2回引いてしまえ、そのあと、引きすぎた 1 を戻そう
という計算をするのです。

計算式にすれば、
79×79 = 80×80 - 80 - 80 + 1
= 6400 - 160 + 1
= 6241
となります。
80を2回引く、というのは 頭の中のイメージ であって、もちろん計算上は、
79×79 = 80×80 - 80 × 2 + 1
= 6400 - 160 + 1
= 6241
これで、良いと思います。
但し、私の場合は、この計算をするときに上記のような図を頭の中に強烈にイメージし、
実際に 下側、右側、これを「トル」、そしてカドのコマを「戻す」ということをやっているので、
どうしても「80を2回引く」という発想になってしまいます。
もっとスマートに計算出来る方なら、初めから「80×2」でいいと思います。
他の例を見ます: 67×67
もちろん、四角形としては 70×70 を考えます。
但し、前回の場合と違い、70 と 67 の差は 3 あります。

そこで、私のイメージの中では、上記の様ように、67×1 が 縦横 3本ずつ、計六本 出てきます。
右下の「コマ」の中には点線が入っていて、9コマに分かれているというイメージです。
そして、これを70として 6本分、4900 から取っ払う、という感じです。

最後に 9 を戻して計算終了、ということですが、もちろん式としては
67×67 = 70 × 70 - 70 × 6 + 9
= 4900 - 420 + 9
= 4480 + 9
= 4489
となります。
慣れてくれば、四角をイメージしつつも一発で、
67×67 = 4900 - 420 + 9
= 4489
と計算できるようになると思います。
なんだ、最初に紹介した4角形の計算方法と大して変わらないじゃないか、と思われるかも知れませんが、
それほど、4角形をイメージするという手法は、基本であり、応用が効くのだと思います。
以上、例を見た数字は、下一桁が9、7、と10に近い数でした。
もちろん、これが逆に0に近ければ、

より大きな数を考えて、トル、というのではなく、
順当に10の位 と 1の位 で分けた4角形を考えて積み上げるということで良いと思います。
(この場合は、私は 10×3 のイメージでOKなんです
 )
)ただ、ここでもう一つ計算例を出したいと思います。
例えば 36×36 これを (35+1)×(35+1)と考えます。

そこで、35×35 の部分は 速算が効いて 1225 とすぐに判りますから、これを使おうという発想です。
36×36 = 35×35 + 35×2 + 1
= 1225 + 70 + 1
= 1295 + 1
= 1296
これを (30+6)×(30+6)として計算すると、
36×36 = 30×30 + 180×2 + 36
= 900 + 360 + 36
= 1260 + 36
= 1296
となりますね。出来ないこともないですが、前者と比べるとやや忙しいでしょうか。
同様に、34×34なら、35×35を使って、
36×36 = 35×35 - 35×2 + 1
= 1225 - 70 + 1
= 1155 + 1
= 1156
と計算出来ます。これは例としてあげました。

色々な計算方法をあげています。もちろん、どの計算方法が一番良いのか、ということはないと思います。
一つの計算を様々な方法で行うこと自体、面白いな、と感じますし、
新たな見かたをすることによって、違った発見があることがあります。
例えば、今回紹介した計算方法により 27×27 を計算します。
まず 30 という数字を考え、30×30 を踏まえて、
900 から 30 を 6 回引く これに 9 を足す、だな、という形になります。
すると、900-30×6 つまり 900-180=720、プラス 9 となります。
こういう風に入って行くと、27×27=729 という暗記も何となくスムースに行きませんでしょうか。
何か、100の位の10の位の 72 というのが何か必然的に見えてきました。
そもそも 27 は 9 の倍数なので、27 の 2乗 も 9 の倍数であり、下一桁が 9 なので、
残りの720の部分も 9 の倍数、ということもありましょうが、
何と、900-180 という求め方がある、と考えたら、覚えやすいですよね。
こういう風にああでもない、こうでもないと考えていると、27の2乗は、729 以外にあり得ない、
そう思えてきます。
そんなこと言ったら、どんな数だって2乗の数は決まっていて、それ以外にあり得ないのですが、ともかくも、
そういう風に思えてくるということです。
次回にこの計算方法を用いた暗記リストを提示します。
数字の動きを見ることによって、上記の 27 の例の様に、何か引っかかる部分が出てくると思います。
それが以外に暗記の役にたつのでは、と考えます。