<<2乗の数即算法>> 続きです。


次に、2乗の数の即算法を具体的に考えます。まずは、観察から入ります。
これまでに、
2乗をすると下二桁が同じになる25以下の数の求め方を考えました。
そこで、その25以下の数の2乗を、実際に対応する数の2乗から引いて見ましょう。
先ずは、各数の2乗の数から「2乗をすると下二桁が同じになる25以下の数の2乗」を引いてみます。
少なくとも、下二桁は同じですから、引き算すれば下二桁は00、すなわち100の倍数にはなるはずです。
最初に、26を考えます
26×26 : 676 - 576 = 100
ここで、676 はもちろん 26の2乗、
576 は 24 の2乗 です。
その差を取ると 100 でした。
さらに26から幾つか、順に見て行きます。
26×26 : 676 - 576 = 100
27×27 : 729 - 529 = 200
28×28 : 784 - 484 = 300
29×29 : 841 - 441 = 400
30×30 : 900 - 400 = 500
31×31 : 961 - 361 = 600
32×32 : 1024 - 324 = 700
33×33 : 1089 - 289 = 800
34×34 : 1156 - 256 = 900
35×35 : 1225 - 225 = 1000
36×36 : 1296 - 196 = 1100
。。。
こうしてみると、単に100の倍数というだけでなく、きちんと規則的に並んでいます。
どうやら 26 以降の2乗の数というのは、以下の形で書き表すことが出来そうです。
(2乗の数)= (何か規則性のある100の倍数)
+ 「2乗をすると下二桁が同じになる25以下の数」の2乗
そこで、実際にこの形に並べ直して見ましょう。
26×26 = 100 + 576 = 676
27×27 = 200 + 529 = 729
28×28 = 300 + 484 = 784
29×29 = 400 + 441 = 841
30×30 = 500 + 400 = 900
31×31 = 600 + 361 = 961
32×32 = 700 + 324 = 1024
33×33 = 800 + 289 = 1089
34×34 = 900 + 256 = 1156
35×35 = 1000 + 225 = 1225
36×36 = 1100 + 196 = 1296
37×37 = 1200 + 169 = 1369
。。。
これを見る限り、(なにか規則性のある100の倍数)とは、
元の数から25を引いた数の100倍ではないか、と判ります。

確かめてみましょう; 元の数を a、b を整数とします。
ここで、「2乗をすると下二桁が同じになる25以下の数」の求め方が、
元の数の範囲によって異なっていたことに注意して場合分けします。
先ず、
a が 25以上50以下のとき、これを見ます。
この時、
「2乗をすると下二桁が同じになる25以下の数」は 50-a で表わせました。
よって、上記の式にあてはめます。
元の数aの2乗= 100のb倍の数 + (50-元の数a)の2乗
a^2= b×100 + (50-a)^2
a^2 = 100b + 2500 -100a + a^2
100b = 100(a-25)
すなわち b = a-25
となります。確かに25を引いた数になりました。
つまり、こういうことです。
2乗の数:
(元の数-25)×100 + (50-元の数)の2乗
となります。まずは、これを覚えて下さい。

(やっと出ました、計算法)
部分的ですが、計算式を記述します。
32×32 = (32-25)×100 + (50-32)^2
= 7 ×100 + 18 × 18
= 700 + 324
= 1024
33×33 = (33-25)×100 + (50-33)^2
= 8 ×100 + 17 × 17
= 800 + 289
= 1089
34×34 = (34-25)×100 + (50-34)^2 = 1156
35×35 = (35-25)×100 + (50-35)^2 = 1225
36×36 = (36-25)×100 + (50-36)^2 = 1296
37×37 = (37-25)×100 + (50-37)^2 = 1369
38×38 = (38-25)×100 + (50-38)^2 = 1444
この様に2乗の数は、
「25を引いて百倍」 と
「50から引いて2乗」 の合計、
という形であらわすことが出来ます。

次に、同様に、
元の数が50から75の場合を見てみましょう。
この場合、
「2乗をすると下二桁が同じになる25以下の数」は 元の数-50 となります。
よって、関係式は
元の数aの2乗= 100のb倍の数 + (元の数a-50)の2乗
と表わせます。
a^2= b×100 + (a-50)^2
a^2 = 100b + 2500 -100a + a^2
100b = 100(a-25)
すなわちb = a-25
となります。50以下の数の場合と同様、元の数から25を引いた数になりました。
つまり、こういうことです。
2乗の数:
(元の数-25)×100 + (元の数-50)の2乗
計算例を見てみます。
51×51 = (51-25)×100 + (51-50)^2
= 26 × 100 + 1 × 1
= 2600 + 1
= 2601
52×52 = (52-25)×100 + (52-50)^2
= 27 × 100 + 2 × 2
= 2700 + 4
= 2704
63×63 = (63-25)×100 + (63-50)^2
= 38 × 100 + 13 × 13
= 3800 + 169
= 3969
正しく計算されていると思います。

では最後に、
元の数が75を超える場合を見ます。
この場合、
「2乗をすると下二桁が同じになる25以下の数」は 100-元の数 でした。
よって、関係式は
(元の数a)の2乗= 100のb倍の数 + (100-元の数a)の2乗
となります。これを展開すると。。
a^2= b×100 + (100-a)^2
a^2= 100b + 10000-200a+a^2
100b = 100(2a-100)
b = 2a-100
と、ここで、100の倍数部分の計算方法が変わってきました。
2a-100 ですから 2倍して100を引く、ということになります。
よって、76以上の数の場合は
2乗の数:
(元の数×2-100)×100 +(100-元の数)の2乗 となります。
76×76 = (76×2-100)×100 + (100-76)^2
( 152-100)×100 + 24 × 24
= 52 ×100 + 576
= 5200 + 576
= 5776
77×77 = (77×2-100)×100 + (100-77)^2
( 154-100)×100 + 23 × 23
= 54 ×100 + 529
= 5400 + 576
= 5929
。。。
まとめると、
「2倍して最初の1を取って百倍」 と 「100から引いて2乗」 の合計、
ですね。



以上が2乗の数の計算法 その1 となります。(その2があります)
ここまでの内容に対し、以下、2、3の補足をしたいと思います。
1: 1の位の数が 5 の数の2乗 は 別途即算法の対象となる
(10の位の数)×(10の位の数+1)×100 + 25
例: 65×65 = 6×7×100 + 25 = 4225
2: 40台の数の2乗、50台の数の2乗、90台の数の2乗については
「2桁の数の2乗 暗記法 その1」 を参照。
上記2に示された計算法とどちらが速いか、しっくり来る方を押さえれば良いと考えます。
3: 計算式の適用についての補足
26から50までの数を対象とした2乗の数の計算式、
(元の数-25)×100 + (50-元の数)の2乗
この計算式自体は、50を超える数、75を超える数でも 実は 正しい答えを導けます。
例1: 51以上75までの数
68×68 = (68-25)×100 + (50-68)^2
= 43 × 100 + (-18) × (-18)
= 4300 + 324
= 4624
この場合、「50-元の数」の部分でマイナスの数になってしまいますが、
2乗するので結局同じことになるのです。
ただし、考え方としては、「元の数-50」から入るのが正しいと思います。
例2: 75を超える数
83×83 = (83-25)×100 + (50-83)^2
= 58 × 100 + (-33) × (-33)
= 5800 + 1089
= 6889
(50-元の数)の2乗の部分が、2乗すると下二桁が同じになる数のうち、25以下ではない、
2番目に大きい数の2乗と等しくなっています。
これも、一旦マイナスの数として計算されるものの、2乗するためにプラスになり、その様になります。
よって、この2乗の部分が 33×33=1089、いう形で、
本来適用すべき計算式である 17×17=289 よりも 800 大きくなっています。
しかし、逆に100の倍数部分は 5800 と計算され、(83×2-100)×100 と計算する
6600 よりも 800 少なくなっています。
だから、結局同じ結果になっているのです。
一見、不思議かも知れませんが、これは逆に導けない方がおかしいわけです。
以上を踏まえると、場合分けに関しても簡素化することも出来ます。
つまり、50から75までの数の計算においては、50以下の計算方法を用いても、
発生するマイナスの数は2乗されプラスに戻って結局同じ、という風に考えれば、
この計算法も単純に75以下とそれ以上に分けて、
75以下の場合、25を引いて100倍、それに 50から引いた数の2乗を足す 、
75以下の場合、2倍して左の1を取って100倍、それに100との差の2乗を足す、
この様にしても良いかも知れません。















 ふぅーっ。。。
ふぅーっ。。。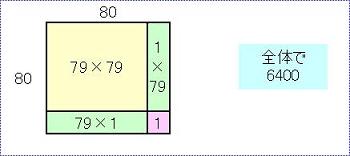
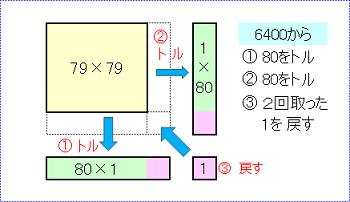

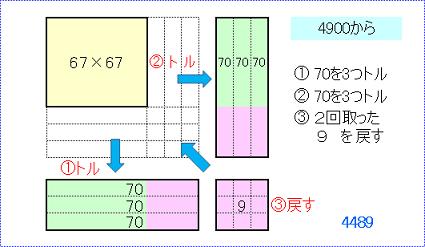






 (これ、速い!)
(これ、速い!)

 (やっと出ました、計算法)
(やっと出ました、計算法)
















