不思議な感覚のする掛け算

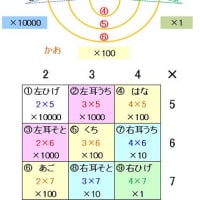
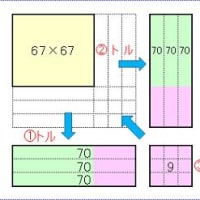
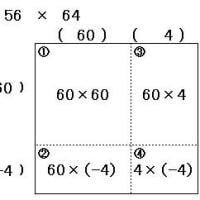
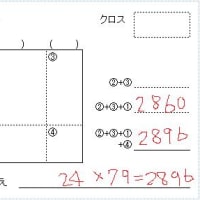
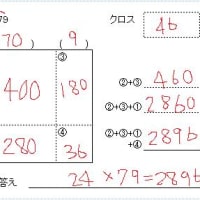
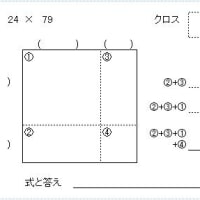
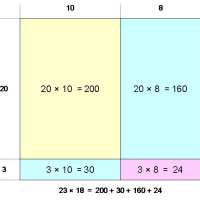
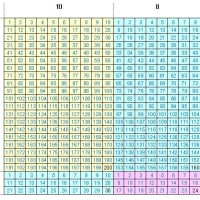
１００との差分を利用する計算法のための練習問題です。

次の４つの掛け算ですが、何となく規則的に並んでいる感じです。
（答えは白文字表示してあります。）


　１２２　×　１７８　＝　２１７１６

　１２４　×　１７６　＝　２１８２４

　１２６　×　１７４　＝　２１９２４

　１２８　×　１７２　＝　２２０１６


これを暗算してみると、何となく不思議に感じると思います。

１００台同士の掛け算の式の中から、練習問題として良いと思われるある条件を考え、
絞り込んでみたのですが、たまたま　２つ飛びで４つ並びました。

前後を入れ替えたものを別とすると、その条件に該当する式は、他にはないんです。
これ、何故そうなったのか、考えるとまた深みにハマりそうです。


あと、問題としては、このあたり。。

　１５１　×　１９９　＝　３００４９

　１５２　×　１９８　＝　３００９６
　　
　１６５　×　１８５　＝　３０５２５

　１７２　×　１７８　＝　３０６２１

（下二桁同士の掛け算に速算法を使えるパターンです。）

　１２１　×　１７９　＝　２１６５９

　１１２　×　１８８　＝　２１０５６

（豪快な繰り上がりがないパターン）


以上、計算練習してみて下さい。

下の方（↓）に、答えを再掲示致します。

　





























　問題と答え

　１２２　×　１７８　＝　２１７１６

　１２４　×　１７６　＝　２１８２４

　１２６　×　１７４　＝　２１９２４

　１２８　×　１７２　＝　２２０１６

　１５１　×　１９９　＝　３００４９

　１５２　×　１９８　＝　３００９６
　　
　１６５　×　１８５　＝　３０５２５

　１７２　×　１７８　＝　３０６２１