1の位の数ごとにまとめていますので、リズム良く計算してみて下さい。
2桁の数の2乗の計算方法 (移動砲!)
<< 1 の列 >>
右から左へ 1 移動して 1 の 2乗 を足す。
← 1 + 1
11×11 = 12×10 + 1 = 121
21×21 = 22×20 + 1 = 441
31×31 = 32×30 + 1 = 961
41×41 = 42×40 + 1 = 1681
51×51 = 52×50 + 1 = 2601
61×61 = 62×60 + 1 = 3721
71×71 = 72×70 + 1 = 5041
81×81 = 82×80 + 1 = 6561
91×91 = 92×90 + 1 = 8281
<< 2 の列 >>
右から左へ 2 移動して 2 の 2乗 を足す。
← 2 + 4
12×12 = 14×10 + 4 = 144
22×22 = 24×20 + 4 = 484
32×32 = 34×30 + 4 = 1024
42×42 = 44×40 + 4 = 1764
52×52 = 54×50 + 4 = 2704
62×62 = 64×60 + 4 = 3844
72×72 = 74×70 + 4 = 5184
82×82 = 84×80 + 4 = 6724
92×92 = 94×90 + 4 = 8464
<< 3 の列 >>
右から左へ 3 移動して 3 の 2乗 を足す。
← 3 + 9
13×13 = 16×10 + 9 = 169
23×23 = 26×20 + 9 = 529
33×33 = 36×30 + 9 = 1089
43×43 = 46×40 + 9 = 1849
53×53 = 56×50 + 9 = 2809
63×63 = 66×60 + 9 = 3969
73×73 = 76×70 + 9 = 5329
83×83 = 86×80 + 9 = 6889
93×93 = 96×90 + 9 = 8649
<< 4 の列 >>
右から左へ 4 移動して 4 の 2乗 を足す。
← 4 + 16
14×14 = 18×10 + 16 = 196
24×24 = 28×20 + 16 = 576
34×34 = 38×30 + 16 = 1156
44×44 = 48×40 + 16 = 1936
54×54 = 58×50 + 16 = 2916
64×64 = 68×60 + 16 = 4096
74×74 = 78×70 + 16 = 5476
84×84 = 88×80 + 16 = 7056
94×94 = 98×90 + 16 = 8836
<< 5 の列 >>
右から左へ 5 移動して 5 の 2乗 を足す。
← 5 + 25
15×15 = 20×10 + 25 = 225
25×25 = 30×20 + 25 = 625
35×35 = 40×30 + 25 = 1225
45×45 = 50×40 + 25 = 2025
55×55 = 60×50 + 25 = 3025
65×65 = 70×60 + 25 = 4225
75×75 = 80×70 + 25 = 5625
85×85 = 90×80 + 25 = 7225
95×95 = 100×90 + 25 = 9025
<< 6 の列 >>
左から右へ 4 移動して 4 の 2乗 を足す。
4 → + 16
16×16 = 12× 20 + 16 = 256
26×26 = 22× 30 + 16 = 676
36×36 = 32× 40 + 16 = 1296
46×46 = 42× 50 + 16 = 2116
56×56 = 52× 60 + 16 = 3136
66×66 = 62× 70 + 16 = 4356
76×76 = 72× 80 + 16 = 5776
86×86 = 82× 90 + 16 = 7396
96×96 = 92×100 + 16 = 9216
<< 7 の列 >>
左から右へ 3 移動して 3 の 2乗 を足す。
3 → + 9
17×17 = 14× 20 + 9 = 289
27×27 = 24× 30 + 9 = 729
37×37 = 34× 40 + 9 = 1369
47×47 = 44× 50 + 9 = 2209
57×57 = 54× 60 + 9 = 3249
67×67 = 64× 70 + 9 = 4489
77×77 = 74× 80 + 9 = 5929
87×87 = 84× 90 + 9 = 7569
97×97 = 94×100 + 9 = 9409
<< 8 の列 >>
左から右へ 2 移動して 2 の 2乗 を足す。
2 → + 4
18×18 = 16× 20 + 4 = 324
28×28 = 26× 30 + 4 = 784
38×38 = 36× 40 + 4 = 1444
48×48 = 46× 50 + 4 = 2304
58×58 = 56× 60 + 4 = 3364
68×68 = 66× 70 + 4 = 4624
78×78 = 76× 80 + 4 = 6084
88×88 = 86× 90 + 4 = 7744
98×98 = 96×100 + 4 = 9604
<< 9 の列 >>
左から右へ 1 移動して 1 の 2乗 を足す。
1 → + 1
19×19 = 18× 20 + 1 = 361
29×29 = 28× 30 + 1 = 841
39×39 = 38× 40 + 1 = 1521
49×49 = 48× 50 + 1 = 2401
59×59 = 58× 60 + 1 = 3481
69×69 = 68× 70 + 1 = 4761
79×79 = 78× 80 + 1 = 6241
89×89 = 88× 90 + 1 = 7921
99×99 = 98×100 + 1 = 9801
<< 9 の列 別表 >>
1つ多い数の2乗 から 1つ多い数の2倍を 引いて 1 を足す。
19×19 = 400 - 40 + 1 = 361
29×29 = 900 - 60 + 1 = 841
39×39 = 1600 - 80 + 1 = 1521
49×49 = 2500 - 100 + 1 = 2401
59×59 = 3600 - 120 + 1 = 3481
69×69 = 4900 - 140 + 1 = 4761
79×79 = 6400 - 160 + 1 = 6241
89×89 = 8100 - 180 + 1 = 7921
99×99 =10000 - 200 + 1 = 9801
(解説別途)















 (これ、速い!)
(これ、速い!)



 (やっと出ました、計算法)
(やっと出ました、計算法)
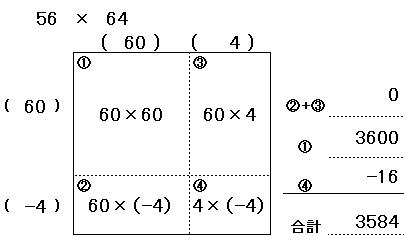








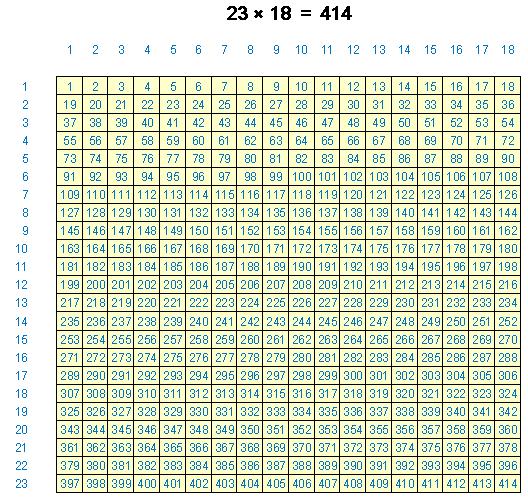
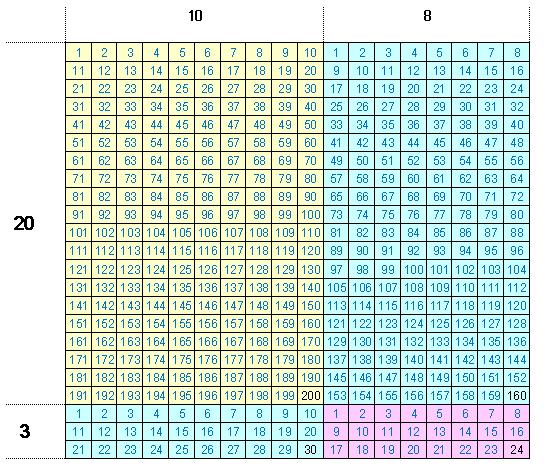
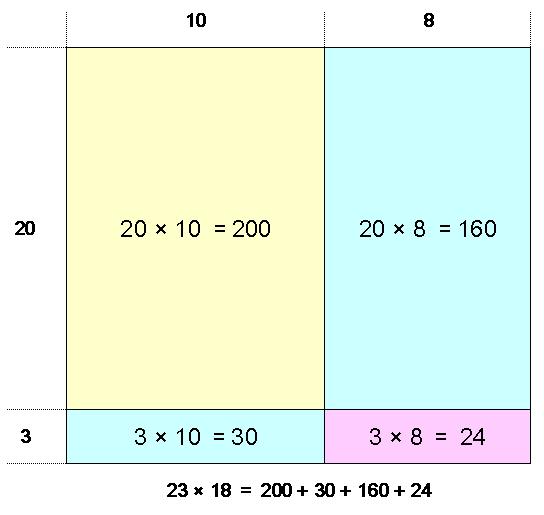




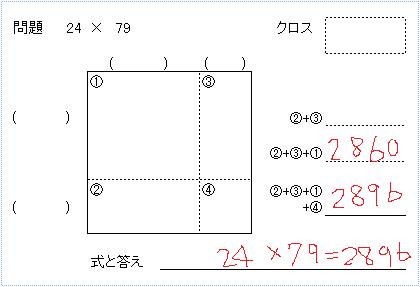
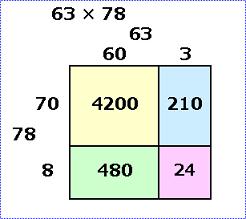





 究極の2桁掛け算暗算法
究極の2桁掛け算暗算法 。「ねこ掛け算」では3桁の掛け算の暗算が出来るようになります。
。「ねこ掛け算」では3桁の掛け算の暗算が出来るようになります。















