不思議な感覚のする掛け算 続き

前々回、不思議な感じがする掛け算として例題を挙げました。
この例題ですが、そもそもどのようにして問題を選んだかというと、

１００台同士の掛け算のなかで、
　１．　下二桁同士の掛け算の積　が　そのまま積の下４桁　になる。
　２．　かつ、下一桁同士の積　も　そのまま下二桁の数　になる。
というものでした。

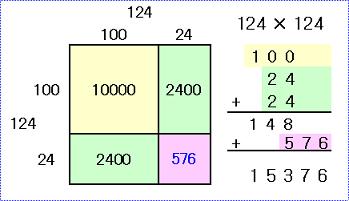
例えば、例に挙げた　１２２　×　１７８　なら、

　下二桁同士の掛け算　２２×７８　の積　は　１７１６
　ですが、これはそのまま
　１２２　×　１７８　の積の下四桁　になります。

　すなわち　２１７１６

これは、掛ける数、掛けられる数の　下二桁の合計　が　１００　
の場合にその様になります。

　　　２２＋７８＝　１００　。。。です。

つまり、基準値１００、差分との合計は　２００、これに　基準値　１００　を掛けると
２００００　となります。よってこれに　差分の積　を加える際、
そのまま下四桁にあてることが出来る、ということです。（。。。）

　１２２　×　１７８　＝　（１００＋２２＋７８）×１００　＋　２２×７８
　　　　　　　　　　　＝　　２００　×１００　＋　２２×７８
　　　　　　　　　　　＝　　２００００　　　　＋　１７１６

また、「かつ、下一桁同士の積　も　そのまま下二桁の数　になる」　というのは、

　下一桁同士の積　２　×　８　＝　１６　　⇒　　２１７１６　の下二桁

ということです。
これも、こうなっていると下二桁同士の掛け算をするときに簡単だろうと考えたわけです。

それで、どういう二桁掛け算がそうなるのか、というと「クロス掛け算」でいうところの　
クロスが１０の倍数の場合です。

すなわち、計算式の　内側の数同士の積 ＋ 外側の数同士の積　これが１０の倍数に
なっていた場合、下一桁同士の積が　その計算の積の下二桁になります。

　２２×７８　＝　（２×７＋２×８）×１０　＋　２０×７０　＋　２×８
　　　　　　　＝　３０　×　１０　＋　１４００　＋　１６
　　　　　　　　　　↑１０の倍数
　　　　　　　＝　３００　＋　１４００　＋　１６
　　　　　　　＝　１７１６

ということで、この２つの条件を満たしていれば、１００との差分を使って計算する方法の
練習問題としては、計算もしやすく、とっかかりとしては良いだろうと考えたわけです。

そして実際その条件に当てはまる式を絞り込んだところ、

　１２２　×　１７８　＝　２１７１６
　１２４　×　１７６　＝　２１８２４
　１２６　×　１７４　＝　２１９２４
　１２８　×　１７２　＝　２２０１６
この４つが綺麗に並んだんです。うーむ。。。

下二桁を足すと合計が　１００　になるというのは　１０１×１９９　から　１５０×１５０　まで、
前後を逆にする場合をカウントしないとすると、５０　通りあります。
　
そのうち、クロスが１０の倍数になるというのは、この２つ飛びの４通りと、１１０×１９０
などのそもそも１０の倍数の計算、これ以外にありませんでした。

　１１０　×　１９０　＝　２０９００
　１２０　×　１８０　＝　２１６００
　１２２　×　１７８　＝　２１７１６
　１２４　×　１７６　＝　２１８２４
　１２６　×　１７４　＝　２１９２４
　１２８　×　１７２　＝　２２０１６
　１３０　×　１７０　＝　２２１００
　１４０　×　１６０　＝　２２４００
　１５０　×　１５０　＝　２２５００
　
この条件を満たす式が、１２０台の掛け算に集中しており、かつ二つ飛び、
というのが何かやたら不思議に思えました。
そもそも、クロスの計算の仕方など、それぞれバラバラに見えます。

　２２×７８　→　２×７　＋　８×２　＝　１４　＋　１６　＝　３０
　２４×７６　→　４×７　＋　６×２　＝　２８　＋　１２　＝　４０
　２６×７４　→　６×７　＋　４×２　＝　４２　＋　　８　＝　５０
　２８×７２　→　８×７　＋　２×２　＝　５６　＋　　４　＝　６０

しかし、すべて綺麗に１０の倍数になります。
どこで、どうやって調整されるのだろう？　という感じです。

この様な条件を満たす式が、１２０台のみ、しかも偶数の場合だけなのは、何故なのか？
考えるのは止めようと思いましたが、やっぱり、考えてしまいました。

　　

上記の条件を満たす下二桁同士の掛け算、すなわち２桁の数同士の掛け算を考えます。

上記の条件とは　
　　掛けられる数と掛ける掛ける数の合計が１００　であることと、
　　両者の内側の数同士の積と外側の数同士の積の和　が１０　の倍数であること
です。

そこで、掛けられる数と掛ける数を入れ替えれば同じ計算とみなすので、

掛けられる数　を　５０　以下の整数とし、１０ａ＋ｂ　とします。
ここで、　ａ　は　０　から　４　までの整数　または　５　とし、
　ｂ　は　ａ　が　４　以下の場合、０　から　９　までの整数、
　　　　　ａ　が　５　の場合、０　とします。

掛ける数と掛けられる数は合計すると　１００　であることから、
掛けられる数は　１０（９－ａ）＋１０－ｂ　と表わすことが出来る。

よって、　（１０ａ＋ｂ）×（１０（９－ａ）＋１０－ｂ）　という計算において、
下二桁同士の積　ｂ×（１０－ｂ）がそのまま全体の積の下二桁になるためには、

　ｂ×（９－ａ）＋　ａ×（１０－ｂ）　が　１０の倍数となれば良い。
　
この数をＣと置き、展開すると

　Ｃ　＝　ｂ×（９－ａ）＋　ａ×（１０－ｂ）
　　　＝　９ｂ　－　ａｂ　＋　１０ａ　－　ａｂ
　　　＝　１０ａ　＋　９ｂ　－　２ａｂ
　　　＝　１０ａ　＋　ｂ（９－２ａ）

ここで、１０ａ　は　１０の倍数　であることより

ｂ×（９－２ａ）　が　０　または、１０の倍数であれば、Ｃ　は　１０の倍数

ここで場合分けを行う

（１）ｂ×（９－２ａ）　が　０　であるとき
　　　９－２ａ　は　０　たりえないので、ｂ＝０
　　　よって　ｂ＝０　の時　Ｃ　は１０の倍数　・・・（１）

（２）ｂ×（９－２ａ）　が　０　でないとき

　　１０の倍数　は　９　以下の整数によって、
　　５×（偶数）　または　（偶数）×５　と表わせるから、

　　　　　　ｂ＝５　　かつ　９－２ａ　が　偶数、
　　または、
　　　　　　ｂが偶数　かつ　９－２ａ　＝　５　であること

　　が　Ｃ　が１０の倍数であることの条件。

ここで、９－２ａ　は奇数であることから、前者の条件は成立せず、
ｂ　が　５　の場合、Ｃは１０の倍数とはならない。

また、後者の条件より、ｂ　は　偶数たりえる一方、
　　　　　９－２ａ＝５　より
　　　　　　　２ａ＝４
　　　　　　　ａ＝２
よって、ｂ　が偶数　かつ　ａ＝２　のとき　Ｃ　は１０の倍数・・・（２）

（１）、（２）を　総合し、この条件を満たす掛けられる数　１０ａ＋ｂ　とは

　ｂが０の場合、ａ　は　０　から　４　までの整数　または　ｂ＝０　の場合　５　より
　　１０ａ＋ｂ　→　０、１０、２０、３０、４０、５０

　ｂが偶数の場合、ａ　は　２　に限定され、
　　１０ａ＋ｂ　→　２２、２４、２６、２８

よって、求められる計算式は

　１０　×　９０　＝　　９００
　２０　×　８０　＝　１６００
　２２　×　７８　＝　１７１６
　２４　×　７６　＝　１８２４
　２６　×　７４　＝　１９２４
　２８　×　７２　＝　２０１６
　３０　×　７０　＝　２１００
　４０　×　６０　＝　２４００
　５０　×　５０　＝　２５００

以上、９通り。

　　

こういう風に計算すると、きちんと　２０台の数の偶数　という形は出てくるんですね。
自分でも、「ふぅーん。。。」と思った次第でした。

ただ、最初に感じた「不思議感」はあまり解消されませんね。
良く分からないけれども、そういうものか、と受け入れる以外ないですね。

数学 ブログランキングへ



　

不思議な感覚のする掛け算

１００との差分を利用する計算法のための練習問題です。

次の４つの掛け算ですが、何となく規則的に並んでいる感じです。
（答えは白文字表示してあります。）


　１２２　×　１７８　＝　２１７１６

　１２４　×　１７６　＝　２１８２４

　１２６　×　１７４　＝　２１９２４

　１２８　×　１７２　＝　２２０１６


これを暗算してみると、何となく不思議に感じると思います。

１００台同士の掛け算の式の中から、練習問題として良いと思われるある条件を考え、
絞り込んでみたのですが、たまたま　２つ飛びで４つ並びました。

前後を入れ替えたものを別とすると、その条件に該当する式は、他にはないんです。
これ、何故そうなったのか、考えるとまた深みにハマりそうです。


あと、問題としては、このあたり。。

　１５１　×　１９９　＝　３００４９

　１５２　×　１９８　＝　３００９６
　　
　１６５　×　１８５　＝　３０５２５

　１７２　×　１７８　＝　３０６２１

（下二桁同士の掛け算に速算法を使えるパターンです。）

　１２１　×　１７９　＝　２１６５９

　１１２　×　１８８　＝　２１０５６

（豪快な繰り上がりがないパターン）


以上、計算練習してみて下さい。

下の方（↓）に、答えを再掲示致します。

　





























　問題と答え

　１２２　×　１７８　＝　２１７１６

　１２４　×　１７６　＝　２１８２４

　１２６　×　１７４　＝　２１９２４

　１２８　×　１７２　＝　２２０１６

　１５１　×　１９９　＝　３００４９

　１５２　×　１９８　＝　３００９６
　　
　１６５　×　１８５　＝　３０５２５

　１７２　×　１７８　＝　３０６２１

　
　　　

少し頑張れば出来る！ １００台の数同士の暗算

ここで、差分による計算法をつかって、１００以上の数の２乗　並びに　１００台同士の数の掛け算　
を具体的に考えてみます。

方法としては、もちろん、１００との差分　をとって考えてます。

先ず、２乗の方から考えます。

例は　１２４　×　１２４

差分をとって考えれば、

　　　（１００＋２４＋２４）×１００　＋　２４×２４
　　＝　１４８×１００　＋　５７６
　　＝　１５３７６

となります。４つの四角形で表わしてみましょう。



この図でも判ります通り、１２４　の　２乗　と　２４　の　２乗　は下二桁が同じですよね。
先に３つの四角形の合計　（１００００＋２４００＋２４００）　を出したら、あと、５７６　を足すわけですが、
桁同士がぶつかって実際に足し算をするのは１００の位（または１０００の位）です。

つまり、１４８　に　５　を足す計算を考えれば良いわけです。

意外と、簡単でしょう。

　　

さらに、１００台同士の数の掛け算一般を考えます。
別に、変わったところはありません。



例は　１３１　×　１２３　ですが、

この場合、３１　×　２３　を　最初に計算しておいた方がいいでしょう。これを先にやって、ちょっと覚えておく。

あとは、１３１　に　２３　を足して　１００倍　すなわち　１５４００　を考えて、覚えておいた　７１３　を足す。

答えは　１６１１３


あるいは、１４７　×　１６８　でしたら

まず、４７　×　６８　を考えて。。。　
　　　　　　　
　　　　　　７×６　＋　４×８　＝４２＋３２＝７４　内側同士と外側同士、それぞれ掛けて足す
　　　　　　７４×１０＝７４０　　　　　　　　それを１０倍する
　　　　　　２４００＋７４０＝３１４０　　　　それに１０の位同士の積を足す
　　　　　　３１４０＋５６　＝　３１９６　　　それに１の位同士の積を足す
　
　　３１９６　これを覚えておいて。。。

１４７＋６８　＝　２１５　　⇒　２１５００

　これに　３１９６　を　位どりに注意しながら足す

　　　２１５００
　　　　３１９６
　　　２４６９６　　　答えは　２４６９６

少し、集中力と注意力が要りますが、やってやれない計算ではありませんね。

　

この計算法になれるための方法が一つあります。

それは、１０１×１０１、１０２×１０２、１０３×１０３。。。と順に暗算して行くのです。

最初は簡単なんですよ。。。

　１０１×１０１　＝　　１０２０１　　（１０２００　＋　　１）
　１０２×１０２　＝　　１０４０４　　（１０４００　＋　　４）
　１０３×１０３　＝　　１０６０９　　（１０６００　＋　　９）
　１０４×１０４　＝　　１０８１６　　（１０８００　＋　１６）
　１０５×１０５　＝　　１１０２５　　（１１０００　＋　２５）
　１０６×１０６　＝　　１１２３６　　（１１２００　＋　３６）
　１０７×１０７　＝　　１１４４９　　（１１４００　＋　４９）
　１０８×１０８　＝　　１１６６４　　（１１６００　＋　６４）
　１０９×１０９　＝　　１１８８１　　（１１８００　＋　８１）

　　楽勝です。

しかし、だんだん、最後の２乗の足し算のところで１００の位への繰り上がりが起きてきます。
最初は１だけですが、

　１１１×１１１　＝　　１２３２１　　（１２２００　＋　１２１）
　１１２×１１２　＝　　１２５４４　　（１２４００　＋　１４４）
　１１３×１１３　＝　　１２７６９　　（１２６００　＋　１６９）
　１１４×１１４　＝　　１２９９６　　（１２８００　＋　１９６）

次第に、繰り上がる数も増えます。

　１１５×１１５　＝　　１３２２５　　（１３０００　＋　２２５）
　１１６×１１６　＝　　１３４５６　　（１３２００　＋　２５６）
　１１７×１１７　＝　　１３６８９　　（１３４００　＋　２８９）
　１１８×１１８　＝　　１３９２４　　（１３６００　＋　３２４）
　１１９×１１９　＝　　１４１６１　　（１３８００　＋　３６１）
　１２０×１２０　＝　　１４４００　　（１４０００　＋　４００）
　１２１×１２１　＝　　１４６４１　　（１４２００　＋　４４１）
　。。。。
　　　　　　　　　　　　　
さらには万の位にも繰り上がり

　１４１×１４１　＝　　１９８８１　　（１８２００　＋　　１６８１）
　１４２×１４２　＝　　２０１６４　　（１８４００　＋　　１７６４）
　１４３×１４３　＝　　２０４４９　　（１８６００　＋　　１８４９）
　。。。。　

後半、終盤はかなりきつくなりますね。

　１８２×１８２　＝　　３３１２４　　（２６４００　＋　　６７２４）
　１８３×１８３　＝　　３３４８９　　（２６６００　＋　　６８８９）
　１８４×１８４　＝　　３３８５６　　（２６８００　＋　　７０５６）
　。。。。

最後はこうなります。

　１９８×１９８　＝　　３９２０４　　（２９６００　＋　　９６０４）
　１９９×１９９　＝　　３９６０１　　（２９８００　＋　　９８０１）
　２００×２００　＝　　４００００　　（３００００　＋　１００００）

これを自分なりにきつくなるところ、「もういいや」というところまで暗算してみます。
計算方法自体にはなれるでしょう。
私は半分位まで行くとかなり考えるなぁ。。という感じになります。

ただ、曲がりなりとも３桁同士の掛け算を暗算でやるわけですから、
今までやったことのない人でしたら「プチ凄いな」感は得られます。

　　
では、以上を踏まえ、以下の計算を暗算してみて下さい。
（答えは白色文字で書いてあります。色を反転させて確認が出来ます。）

　１３５　×　１６５　＝　２２２７５　

　１４２　×　１５８　＝　２２４３６

あっと思った方、この計算法が判った方です。

　
小学校教育 ブログランキングへ

差分による計算法（２）

差分による計算法に関する補足として、基準の数字が掛け算をする数より大きい時、
この計算法を４つの四角形で表わすとどうなるか、ということを考えます。

例えば　９４　×　９７　の場合、



上記の様に差分の（－６）と（－３）を四角形の１辺としてそのままあてがいます。

図としては、マイナスの長さ、あるいは、マイナスの面積、という形になり、その実態は何？と
考えると良く判りませんし、子供に説明しようとしても難しい。

但し、イメージとしてはこの様な計算しても問題は無いですよね。

それで、基準の数で３つの項をくくれます、という部分、下図のように並べ変えると良く分かります。



　　１００×１００＋１００×（－６）＋１００×（－３）　は　ひとまとめにして
　（１００－６－３）×１００　すなわち　９１　×　１００　になります

ということでした。あとは　１８　を足せばよいということになります。

　

差分による計算法（１）

２乗の計算法の２番目として、一の位の数を　片方から片方へ移動させ、移動した分の２乗を加える、
という方法を紹介いたしました。

例えば　３４×３４　なら
　１の位の数　４　を右から左に移動し、その２乗を足す。

　　　３４　×　３４　＝　３８　×　３０　＋　４×４
　　　　　←４←
　　　　　移動！　　　　　　　　　　　＋移動した分の２乗！
　　　　　　　　　　　＝　１１４６　＋　１６　
　　　　　　　　　　　＝　１１５６

これで計算が出来てしまう、ということでした。
さて、これを２乗計算以外の計算にも適用することを考えます。

その場合、単純に一の位の数を移動させて、移動量の２乗と加える、という計算は出来ません。
少し考察を深めましょう。

　　移動砲、万能ならず。。。　　ならば拡散移動砲？　違います。


この１の位の数を移動させるという計算法のポイントは、２桁の掛け算を４つの四角形で考えた場合の
３つの項を一つの数字でくくる　ということでした。
いわゆる「分配法則」をつかって、３つの項をひとまとめにしているので、計算が楽になるのです。

実は、１０の位の数　が同じ数同士の掛け算の場合、その１０の位の数を使って「分配法則」が使えます。

例えば　６２×　６３　の例を考えます。

ここで　６０　という数字に注目し　６２　と　６３　という数字が、
６０　に対してどれだけ差があるのか、という点でとらえます。

それぞれ　６２　は　６０　に対し　＋２　の差分があるので　６０＋２、
　　　　　６３　は　６０　に対し　＋３　の差分があるので　６０＋３
　　　　　（ちょっと、考え方として慣れて下さい）

すると、　

　６２×６３　＝　（６０＋２）×（６０＋３）　　
　　　　　　　＝　６０×６０　＋　２×６０　＋　６０×３　＋　２×３
　　　　　　　＝　（６０＋２＋３）×６０　＋　２×３　・・・式１
　　　　　　　＝　６５×６０　＋　６
　　　　　　　＝　　３９００　＋　６
　　　　　　　＝　　３９０６　

こう表現出来ます。

最後に足し算する部分は　２乗の計算の場合「移動量の２乗」ということでしたが、
この場合は「差分同士の積」となるわけです。

ここで、最初の　６２×６３　という式から　式１　の形まで直接もっていければ、
計算はより容易になりそうです。

そのための一般的な式の見方が以下の通りです。

　　　　　　　６２　×　６３　＝　　（６０＋２＋３）　×　　６０　＋　（＋２）×（＋３）
　　６０：　　＋２　　　＋３
　　基準　　差分　　　差分　　（基準＋差分１＋差分２）×　基準　＋　　差分１×差分２　

先ずは、基準の数（６０）を考え、
その基準の数に対する、掛け算する数の差分をそれぞれ出します。（＋２と＋３）

あとは、式の通り、
基準と二つの差分を足して、基準をかけ、それに差分同士を掛けたものを足す、
これで良いわけです。

その他計算例：　４６×４３　＝　（４０＋６＋３）×４０　＋　６×３
　　　　　　　　　　　　　　＝　４９×４０　＋　１８
　　　　　　　　　　　　　　＝　１９６０　＋　１８
　　　　　　　　　　　　　　＝　１９７８

ここで、頭の体操に近いですが、理解を深めるための考察をします。
実は、この基準の数というものは、必ず１０の位の数にしなければならないということではありません。
例えば最初の計算の場合、基準を　６１　としても良いのです。良いというか、計算間違いにはなりません。
要は、差分がきちんと取れ、その後の計算も正しければ、最終的に同じ答えが出ます。

　　　　　　　６２　×　６３　＝　　（６１＋１＋２）　×　　６１　＋　（＋１）×（＋２）
　　６１：　　＋１　　　＋２
　　基準　　　差分　　　差分　
　　　　　　　　　　　　　　　＝　６４　×　６１　＋　２
　　　　　　　　　　　　　　　＝　３９０４　＋　２
　　　　　　　　　　　　　　　＝　３９０６

しかし、ごらんの通り、計算は全く簡素化されません。もちろん、
わざわざこういう計算をする意味はありませんが、基準を決め、
差分を二項に対しとって計算するという仕組みを理解するため、一度確認をしておいて下さい。

では、次の計算例、基準の数　を　掛け算する数よりも大きい数でとった場合について考えます。

例として　６８×６７　を考えますが、基準は　７０　とします。

　　　　　　　６８　×　６７　＝　　（７０－２－３）　×　　７０　＋　（－２）×（－３）
　　７０：　　－２　　　－３
　　基準　　差分　　　差分　　（基準＋差分１＋差分２）×　基準　＋　　差分１×差分２
　　　　　　　　　　　　　　　＝　６５　×　７０　＋　６
　　　　　　　　　　　　　　　＝　４５５０　＋　６
　　　　　　　　　　　　　　　＝　４５５６

差分がマイナスになりましたが、丁寧に式にあてはめれば、当然計算としても正しくなります。
最後、差分同士の掛け算の部分では、マイナス同士の掛け算となっており、結局足し算になっています。
計算自体も簡素化されたのではないでしょうか。

では、次に、７２×６９　などの例ではどうでしょうか？　１０の位の数は異なります。
ここで、基準を　７０　とします。差分にプラスマイナス両方出るものの、分配法則を使うことはもちろん可能です。　

　　　　　　　７２　×　６９　＝　　（７０＋２－１）　×　　７０　＋　（＋２）×（－１）
　　７０：　　＋２　　　－１
　　　　　　　　　　　　　　　＝　７１　×　７０　＋　２　×（－１）
　　　　　　　　　　　　　　　＝　４９７０　－　２
　　　　　　　　　　　　　　　＝　４９６８

この場合、一方の差分はプラス、もう一方はマイナスですので、最後に引き算をする形となります。
これも場合によっては、クロス掛け算　を行うよりも速いかも知れません。
計算が速くなるケースというのは、必ずしも１０の位の数が同じである必要はなく、
２数が　１０の倍数のような　基準の数字に近く、さらに２数同士もお互い近ければ良い、ということになります。

ここで、以前紹介した「かかし掛け算」について、この「差分による計算」という点から見てみます。
例えば、７３×７９　という計算については、基準は中間の　７６　で取り、開き（＝差分）は　３　ということになります。

　　　　　　　７３　×　７９　＝　　（７６－３＋３）　×　　７６　＋　（－３）×（＋３）
　　７６：　　－３　　　＋３
　　　　　　　　　　　　　　　＝　７６　×　７６　＋　（－３）　×　３
　　　　　　　　　　　　　　　＝　５７７６　－　９
　　　　　　　　　　　　　　　＝　５７６７

最初の基準の数をかける部分は、差分同士が相殺されて、結局　基準の数の２乗　すなわち　中間の数の２乗　になります。
その後、差分同士の掛け算になりますが、片方が正で片方が負となりますので、すなわち２乗を引くということになります。

　　

最後に、二桁掛け算の範囲で、この差分の掛け算が最も使い出がある場合を紹介します。
これまでの内容は忘れてしまっても、むしろここだけは押さえたいです。
それは、１００に近い数同士の掛け算です。すなわち基準が１００になる場合です。
分配法則でくくる部分が　×１００　となるので、あとの差分同士の積の足し算は、
その積の結果をそのまま下二桁の数に出来るのです。

　　　　　　　９７　×　９４　＝　　（１００－３－６）　×　　１００　＋　（－３）×（－６）
　１００：　　－３　　　－６
　　　　　　　　　　　　　　　＝　９１　×　１００　＋　（－３）　×（－６）
　　　　　　　　　　　　　　　＝　９１００　＋１８
　　　　　　　　　　　　　　　＝　９１１８

これは、速算法　ですね。是非、慣れましょう。

　

ちなみに、息子にこの掛け算の方法を教える時、「ディフ掛け算」と呼びました。
差分⇒ディファレンス　だからです。

「ディフ掛け算」は１２４×１０２　などという掛け算もできます。
１２６×１００＋２４×２　で　１２６４８　です。

１２の２乗を暗記している人なら、１１２の２乗だって出来ちゃいます。１２５４４です。

ちょっだけ凄いですね。

次回、差分による計算法（２）　として、補足としてこの計算法を４つの四角形を使って考えます。