「かかし掛け算」について述べます。
覚えておくと非常に2桁掛け算が簡素化する場合が多々あり、便利です。
計算の方法としては、2項の掛け算を
その 中間の値の2乗 と 中間との差の2乗 の 差に置き換える という方法です。
 は。。
は。。
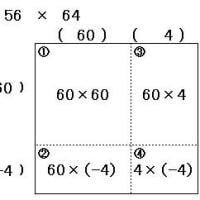
例えば 56 × 64 なら
その 中間の数 60 の2乗 から 中間との差(「開き」) 4 の2乗 を 引けば良い、とういものです。
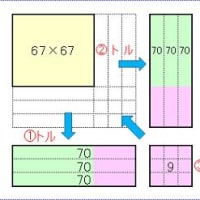
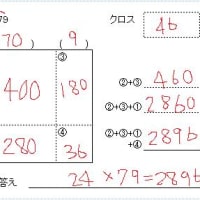
これを4つの四角形で表してみると以下の通りになります。
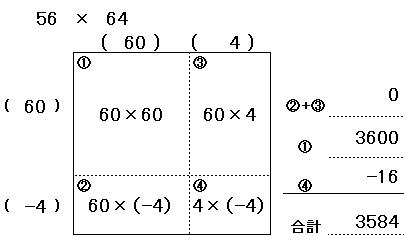
ここで、56 は 60 と (-4)に分解します。60は56と64の中間の数です。
そうなると 左上は60×60、左下と右上は相殺されて0、右下は 4×(-4)となります。
結果、3600-16 で良い、ということになります。
64 の方は 60 と 4 に分けてありますが、これはもちろん、10の位と1の位で分けてあるわけではなく、
60 が中間の数であることによります。
これを、大人は何となく、そうか、と思うかもしれませんが、この説明を小学生に行う場合は、多少難しいところがありますね。
というのも、4つの四角形を使った考え方は、方眼紙を使ってマスの数を数えてその対応を理解させたように、あくまでも正の数を扱うことが前提です。
しかし、ここではマイナスの数を辺の長さにあてたり、実際にマイナスの数を掛けたりと、小学生の算数の世界ではありえないことをします。
よって、小学生にこの計算法を教えるときには、「こうすれば答えがでるのだよ」とやり方のみを納得させるしかないかもしれません。
何故そうなるのか、ということの理解については、何年か先になるかも知れませんが、それはそれで良いと考えます。

この計算法に慣れるためには、以下のことを念頭に置きながら、実際の例を見てみるのが早いでしょう。
1. 二つの数の中間の数をすぐに発見出来るかどうか。
2. 中間の数2乗、開きの数の2乗はすぐ浮かぶか。
3. 「開き」の2乗の数は大きすぎず、「中間」の2乗から引きやすい数かどうか?
そこで先ず、中間の数が 10の倍数 の場合を考えます。
例として中間は 70、「開き」を1ずつ増やしながら実際の計算を見てみます。
少し、丁寧に自分でも計算しながら追いかけてみて下さい。
スタート
: 70 × 70= 4900
1: 69 × 71= 4900 - 1 = 4899
2: 68 × 72= 4900 - 4 = 4896
3: 67 × 73= 4900 - 9 = 4891
4: 66 × 74= 4900 - 16 = 4884
5: 65 × 75= 4900 - 25 = 4875
6: 64 × 76= 4900 - 36 = 4864
7: 63 × 77= 4900 - 49 = 4851 (50を引いて1を足す)
8: 62 × 78= 4900 - 64 = 4836
9: 61 × 79= 4900 - 81 = 4819
10: 60 × 80= 4900 - 100 = 4800
11: 59 × 81= 4900 - 121 = 4779
12: 58 × 82= 4900 - 144 = 4756 (150を引いて6を足す)
14: 56 × 84= 4900 - 196 = 4704 (200を引いて4を足す)
22: 48 × 92= 4900 - 484 = 4416 (500を引いて16を足す)
うーん、こんなにも簡単に計算できてしまうのか、という感じですね。
そこれ、一つ例として以上の 70 を中心とした「かかし掛け算」に慣れておけば、
他の中心が10の倍数の計算に関しても、スムースに計算出来ると思います。
例えば、「開きが14」の場合、「200を引いて4を足す」と覚えておけば、
64×36 など 中心は50、開き14 と見て、
2500-200+4 = 2304 と計算できます。
なにせ、理屈から言って下二桁の数は変わってこないですからね。慣れると速いです。



では次に、中心の数が10の倍数以外、どうするかですね。
これは、2乗の数を暗記しないことには即算が出来ないということになります。
その気になれば簡単に覚えられる、という方もいらっしゃいますが、なかなか、そうもいかないのが現実ですね。
以前の記事でゴロ合わせなるものも紹介しましたが、出来れば数字そのものとして覚えたほうが、計算自体は早くなると考えています。
(というか、自分がそうなんです。ゴロで考えるとそこで計算する頭が一旦止まる感じがするのです。)
この2乗の数の暗記のコツに関しては別途ご紹介申し上げることといたしまして、先ずは計算の実例を見てみましょう。
中心は、78 としましょう。今回は面倒ですので、ざっと見てください。
スタート
: 78 × 78 = 6084
1: 77 × 79 = 6084 - 1 = 6083
2: 76 × 80 = 6084 - 4 = 6080
3: 75 × 81 = 6084 - 9 = 6075
4: 74 × 82 = 6084 - 16 = 6068
5: 73 × 83 = 6084 - 25 = 6059
6: 72 × 84 = 6084 - 36 = 6048
7: 71 × 85 = 6084 - 49 = 6035 (50を引いて1を足す)
8: 70 × 86 = 6084 - 64 = 6020
9: 69 × 87 = 6084 - 81 = 6003
10: 68 × 88 = 6084 - 100 = 5984
12: 66 × 90 = 6084 - 144 = 5940 (150を引いて6を足す)
14: 64 × 92 = 6084 - 196 = 5888 (200を引いて4を足す)
20: 58 × 98 = 6084 - 400 = 5684
以上、開きが 20 までの場合を見ましたが、中心が一般の整数の場合は、
せいぜい開きが 5 ぐらいまでが「かかし掛け算」の対象でしょうか。
あまり中心を探すのに考えてしまったり、引き算が面倒だったりすると、
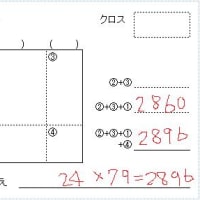
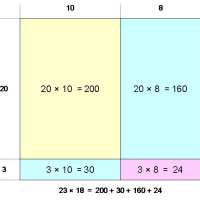
「クロス掛け算」を行った方が結局は早いです。
ただし、開きが 7 の場合(→49を引く=50を引いて1を足す)や、
開きが10、20、または30の場合は、それと気がつけば「かかし掛け算」の対象でしょう。
例1: 32×46 中心 39 開き 7 → 1521- 49 = 1472
例2: 78×98 中心 88 開き 10 → 7744-100 = 7644
例3: 42×82 中心 62 開き 20 → 3844-400 = 3444
例4: 16×76 中心 46 開き 30 → 2116-900 = 1216
いずれにせよ、2乗の掛け算を暗記していることが前提ですが、暗記が完璧になっていれば、
例えば、例2で、「100引けばよい」などというのは見た瞬間に答えが出ているようなものです。
是非マスターしましょう。
その他、留意点としては、この掛け算は「偶数同士」または「奇数同士」の掛け算でなければ使えないということですね。
そうでないと中心の数が整数で出てこないからですね。
しかし、たとえ「奇数×偶数」であっても、以下の通り計算すれば当然計算可能です。
87×84 = 86×84+84 = 7225-1+84 = 7308 という
しかし、これをやる位でしたら、初めから「クロス掛け算」を行った方が個人的には頭が疲れないし、
速い、と思います。


以上、「かかし掛け算」について見てきました。
これが理解できると、例えば、
648×552 なんて言う掛け算も。。。
→ 600×600-48×48 = 360000-2304 = 357696
なんて、出来ますね。(あまり嬉しくありませんが)
次回、2乗計算の暗記のコツについて述べます。

覚えておくと非常に2桁掛け算が簡素化する場合が多々あり、便利です。
計算の方法としては、2項の掛け算を
その 中間の値の2乗 と 中間との差の2乗 の 差に置き換える という方法です。
 は。。
は。。例えば 56 × 64 なら
その 中間の数 60 の2乗 から 中間との差(「開き」) 4 の2乗 を 引けば良い、とういものです。
これを4つの四角形で表してみると以下の通りになります。

ここで、56 は 60 と (-4)に分解します。60は56と64の中間の数です。
そうなると 左上は60×60、左下と右上は相殺されて0、右下は 4×(-4)となります。
結果、3600-16 で良い、ということになります。
64 の方は 60 と 4 に分けてありますが、これはもちろん、10の位と1の位で分けてあるわけではなく、
60 が中間の数であることによります。
これを、大人は何となく、そうか、と思うかもしれませんが、この説明を小学生に行う場合は、多少難しいところがありますね。
というのも、4つの四角形を使った考え方は、方眼紙を使ってマスの数を数えてその対応を理解させたように、あくまでも正の数を扱うことが前提です。
しかし、ここではマイナスの数を辺の長さにあてたり、実際にマイナスの数を掛けたりと、小学生の算数の世界ではありえないことをします。
よって、小学生にこの計算法を教えるときには、「こうすれば答えがでるのだよ」とやり方のみを納得させるしかないかもしれません。
何故そうなるのか、ということの理解については、何年か先になるかも知れませんが、それはそれで良いと考えます。

この計算法に慣れるためには、以下のことを念頭に置きながら、実際の例を見てみるのが早いでしょう。
1. 二つの数の中間の数をすぐに発見出来るかどうか。
2. 中間の数2乗、開きの数の2乗はすぐ浮かぶか。
3. 「開き」の2乗の数は大きすぎず、「中間」の2乗から引きやすい数かどうか?
そこで先ず、中間の数が 10の倍数 の場合を考えます。
例として中間は 70、「開き」を1ずつ増やしながら実際の計算を見てみます。
少し、丁寧に自分でも計算しながら追いかけてみて下さい。
スタート
: 70 × 70= 4900
1: 69 × 71= 4900 - 1 = 4899
2: 68 × 72= 4900 - 4 = 4896
3: 67 × 73= 4900 - 9 = 4891
4: 66 × 74= 4900 - 16 = 4884
5: 65 × 75= 4900 - 25 = 4875
6: 64 × 76= 4900 - 36 = 4864
7: 63 × 77= 4900 - 49 = 4851 (50を引いて1を足す)
8: 62 × 78= 4900 - 64 = 4836
9: 61 × 79= 4900 - 81 = 4819
10: 60 × 80= 4900 - 100 = 4800
11: 59 × 81= 4900 - 121 = 4779
12: 58 × 82= 4900 - 144 = 4756 (150を引いて6を足す)
14: 56 × 84= 4900 - 196 = 4704 (200を引いて4を足す)
22: 48 × 92= 4900 - 484 = 4416 (500を引いて16を足す)
うーん、こんなにも簡単に計算できてしまうのか、という感じですね。
そこれ、一つ例として以上の 70 を中心とした「かかし掛け算」に慣れておけば、
他の中心が10の倍数の計算に関しても、スムースに計算出来ると思います。
例えば、「開きが14」の場合、「200を引いて4を足す」と覚えておけば、
64×36 など 中心は50、開き14 と見て、
2500-200+4 = 2304 と計算できます。
なにせ、理屈から言って下二桁の数は変わってこないですからね。慣れると速いです。



では次に、中心の数が10の倍数以外、どうするかですね。
これは、2乗の数を暗記しないことには即算が出来ないということになります。
その気になれば簡単に覚えられる、という方もいらっしゃいますが、なかなか、そうもいかないのが現実ですね。
以前の記事でゴロ合わせなるものも紹介しましたが、出来れば数字そのものとして覚えたほうが、計算自体は早くなると考えています。
(というか、自分がそうなんです。ゴロで考えるとそこで計算する頭が一旦止まる感じがするのです。)
この2乗の数の暗記のコツに関しては別途ご紹介申し上げることといたしまして、先ずは計算の実例を見てみましょう。
中心は、78 としましょう。今回は面倒ですので、ざっと見てください。
スタート
: 78 × 78 = 6084
1: 77 × 79 = 6084 - 1 = 6083
2: 76 × 80 = 6084 - 4 = 6080
3: 75 × 81 = 6084 - 9 = 6075
4: 74 × 82 = 6084 - 16 = 6068
5: 73 × 83 = 6084 - 25 = 6059
6: 72 × 84 = 6084 - 36 = 6048
7: 71 × 85 = 6084 - 49 = 6035 (50を引いて1を足す)
8: 70 × 86 = 6084 - 64 = 6020
9: 69 × 87 = 6084 - 81 = 6003
10: 68 × 88 = 6084 - 100 = 5984
12: 66 × 90 = 6084 - 144 = 5940 (150を引いて6を足す)
14: 64 × 92 = 6084 - 196 = 5888 (200を引いて4を足す)
20: 58 × 98 = 6084 - 400 = 5684
以上、開きが 20 までの場合を見ましたが、中心が一般の整数の場合は、
せいぜい開きが 5 ぐらいまでが「かかし掛け算」の対象でしょうか。
あまり中心を探すのに考えてしまったり、引き算が面倒だったりすると、
「クロス掛け算」を行った方が結局は早いです。
ただし、開きが 7 の場合(→49を引く=50を引いて1を足す)や、
開きが10、20、または30の場合は、それと気がつけば「かかし掛け算」の対象でしょう。
例1: 32×46 中心 39 開き 7 → 1521- 49 = 1472
例2: 78×98 中心 88 開き 10 → 7744-100 = 7644
例3: 42×82 中心 62 開き 20 → 3844-400 = 3444
例4: 16×76 中心 46 開き 30 → 2116-900 = 1216
いずれにせよ、2乗の掛け算を暗記していることが前提ですが、暗記が完璧になっていれば、
例えば、例2で、「100引けばよい」などというのは見た瞬間に答えが出ているようなものです。
是非マスターしましょう。
その他、留意点としては、この掛け算は「偶数同士」または「奇数同士」の掛け算でなければ使えないということですね。
そうでないと中心の数が整数で出てこないからですね。
しかし、たとえ「奇数×偶数」であっても、以下の通り計算すれば当然計算可能です。
87×84 = 86×84+84 = 7225-1+84 = 7308 という
しかし、これをやる位でしたら、初めから「クロス掛け算」を行った方が個人的には頭が疲れないし、
速い、と思います。


以上、「かかし掛け算」について見てきました。
これが理解できると、例えば、
648×552 なんて言う掛け算も。。。
→ 600×600-48×48 = 360000-2304 = 357696
なんて、出来ますね。(あまり嬉しくありませんが)
次回、2乗計算の暗記のコツについて述べます。