2桁の数の2乗、暗記法もこれで最終回となります。
とは言え、今回はこれまでと比べて、全く緊張感がない内容となります。非常に気楽です。
 ふぅーっ。。。
ふぅーっ。。。
2乗の掛け算を記憶する際に多少の補足的なこと、思い付きを並べます。
かなりどうでも良いことを含みます。
どうでも良いことであっても、何か引っかかって記憶の補助になるかも知れない。
そんな主旨です。
1.2乗すると下二桁の数がもとの数と同じになるもの
→ 25 と 76
25×25= 625
76×76=5776
→ ちなみに 625 は2乗すると 390625 となり、
下三桁に再び 625 が出てくる。
2. ぞろ目 下3桁
→ 38 のみ
38×38 = 1444
3. ぞろ目 下二桁 4がそろう場合あり
12×12 = 144
38×38 = 1444
62×62 = 3844
88×88 = 7744
4. ぞろ目 百の位と十の位: 1,2,4,7,8 がそろう
46×46 = 2116
15×25 = 225
35×35 = 1225
65×65 = 4225
85×85 = 7225
21×21 = 441
38×38 = 1444
76×76 = 5776
83×83 = 6889
5. ぞろ目 千の位と百の位
34×34 = 1156
47×47 = 2209
58×58 = 3364
67×67 = 4489
88×88 = 7744
94×94 = 8836
6. ぞろ目キング(00は除く)
キング: 88×88 = 7744
次点: 38×38 = 1444
※順番、どっちにしようか迷いましたが、やはりその数自身もぞろ目というのが
キングの名に値すると判断しました。
7. 元の数の2つの数字が2乗の数の数字のどこか含まれる
25×25
27×27 = 729
63×63 = 3969
64×64 = 4096
74×74 = 5476
95×95 = 9025
96×96 = 9216
8. 26の2乗には、6が2回出てくる。
26×26 = 676 (だからなに。。)
9. もとの数の数字を足した合計と、2乗の数の数字の合計が等しい
18×18= 324
19×19= 361
45×45= 2025
46×46= 2116
55×55= 3025
90×90= 8100
99×99= 9801
10. 2 の倍数だらけ (偶数兄弟!)
22×22 = 484
68×68 = 4624 (しかも真ん中の 6 と 2 を一緒にすると 484)
11. 3 の倍数だらけ
63×63 = 3969 (これはすごい。。アホになりそう)
12. 両脇の数字が同じ
22×22 = 484
68×68 = 4624 (また、偶数兄弟)
39×39 = 1521
(40×40 = 1600)
41×41 = 1681
75×75 = 5625
97×97 = 9409
13. 元の数を含めて6つの数字が登場
53×53
54×54
57×57
59×59
72×72 = 5184
79×79 = 6241
84×84 = 7056
14. 数字が昇順で登場 (昇り龍!)
13×13 = 169
16×16 = 256
17×17 = 289
37×37 = 1369 4桁ではこれのみ
15. 数字が降順で登場
29×29 = 841
31×31 = 961
16. 逆にすると2乗も逆になる組み合わせ
12×12 = 144
21×21 = 441
13×13 = 169
31×31 = 961
17. 同じ数字が現れる組み合わせ
ダブル
32×32 = 1024
49×49 = 2401
35×35 = 1225
39×39 = 1521
19×19 = 361
56×56 = 3136
34×34 = 1156
81×81 = 6561
64×64 = 4096
98×98 = 9604
37×37 = 1369
44×44 = 1936
7が割り込む!
24×24 = 576
76×76 = 5776
9が割り込む!
23×23 = 529
77×77 = 5929
両脇が入れ替わる!
42×42 = 1764
69×69 = 4761
トリプル
12×12 = 144
21×21 = 441
38×38 = 1444
13×13 = 169
14×14 = 196
31×31 = 961
36×36 = 1296
54×54 = 2916
96×96 = 9216
16×16 = 256
25×25 = 625
75×75 = 5625
18. 暗記する上で、隣り合わせでややこしい。
36×36 = 1296
37×37 = 1369
⇒ 14のトピックも合わせて覚えて間違えないようにしましょう。


以上、が「2乗の数の暗記法」となります。
最悪、ゴロ合わせもある程度ご紹介いたしましたので、御参考になさって下さい。
とは言え、今回はこれまでと比べて、全く緊張感がない内容となります。非常に気楽です。
 ふぅーっ。。。
ふぅーっ。。。2乗の掛け算を記憶する際に多少の補足的なこと、思い付きを並べます。
かなりどうでも良いことを含みます。
どうでも良いことであっても、何か引っかかって記憶の補助になるかも知れない。
そんな主旨です。
1.2乗すると下二桁の数がもとの数と同じになるもの
→ 25 と 76
25×25= 625
76×76=5776
→ ちなみに 625 は2乗すると 390625 となり、
下三桁に再び 625 が出てくる。
2. ぞろ目 下3桁
→ 38 のみ
38×38 = 1444
3. ぞろ目 下二桁 4がそろう場合あり
12×12 = 144
38×38 = 1444
62×62 = 3844
88×88 = 7744
4. ぞろ目 百の位と十の位: 1,2,4,7,8 がそろう
46×46 = 2116
15×25 = 225
35×35 = 1225
65×65 = 4225
85×85 = 7225
21×21 = 441
38×38 = 1444
76×76 = 5776
83×83 = 6889
5. ぞろ目 千の位と百の位
34×34 = 1156
47×47 = 2209
58×58 = 3364
67×67 = 4489
88×88 = 7744
94×94 = 8836
6. ぞろ目キング(00は除く)
キング: 88×88 = 7744
次点: 38×38 = 1444
※順番、どっちにしようか迷いましたが、やはりその数自身もぞろ目というのが
キングの名に値すると判断しました。
7. 元の数の2つの数字が2乗の数の数字のどこか含まれる
25×25
27×27 = 729
63×63 = 3969
64×64 = 4096
74×74 = 5476
95×95 = 9025
96×96 = 9216
8. 26の2乗には、6が2回出てくる。
26×26 = 676 (だからなに。。)
9. もとの数の数字を足した合計と、2乗の数の数字の合計が等しい
18×18= 324
19×19= 361
45×45= 2025
46×46= 2116
55×55= 3025
90×90= 8100
99×99= 9801
10. 2 の倍数だらけ (偶数兄弟!)
22×22 = 484
68×68 = 4624 (しかも真ん中の 6 と 2 を一緒にすると 484)
11. 3 の倍数だらけ
63×63 = 3969 (これはすごい。。アホになりそう)
12. 両脇の数字が同じ
22×22 = 484
68×68 = 4624 (また、偶数兄弟)
39×39 = 1521
(40×40 = 1600)
41×41 = 1681
75×75 = 5625
97×97 = 9409
13. 元の数を含めて6つの数字が登場
53×53
54×54
57×57
59×59
72×72 = 5184
79×79 = 6241
84×84 = 7056
14. 数字が昇順で登場 (昇り龍!)
13×13 = 169
16×16 = 256
17×17 = 289
37×37 = 1369 4桁ではこれのみ
15. 数字が降順で登場
29×29 = 841
31×31 = 961
16. 逆にすると2乗も逆になる組み合わせ
12×12 = 144
21×21 = 441
13×13 = 169
31×31 = 961
17. 同じ数字が現れる組み合わせ
ダブル
32×32 = 1024
49×49 = 2401
35×35 = 1225
39×39 = 1521
19×19 = 361
56×56 = 3136
34×34 = 1156
81×81 = 6561
64×64 = 4096
98×98 = 9604
37×37 = 1369
44×44 = 1936
7が割り込む!
24×24 = 576
76×76 = 5776
9が割り込む!
23×23 = 529
77×77 = 5929
両脇が入れ替わる!
42×42 = 1764
69×69 = 4761
トリプル
12×12 = 144
21×21 = 441
38×38 = 1444
13×13 = 169
14×14 = 196
31×31 = 961
36×36 = 1296
54×54 = 2916
96×96 = 9216
16×16 = 256
25×25 = 625
75×75 = 5625
18. 暗記する上で、隣り合わせでややこしい。
36×36 = 1296
37×37 = 1369
⇒ 14のトピックも合わせて覚えて間違えないようにしましょう。


以上、が「2乗の数の暗記法」となります。
最悪、ゴロ合わせもある程度ご紹介いたしましたので、御参考になさって下さい。












二桁数の2乗
超簡単な暗算法!!!
━・━・━・━・━・━・━・━・━・━・━・━・━・━
※1.以下では,Zの2乗を Z^2 等と表示する。
※2.複号[±)は同順(上なら全ての式で上を
採り,下なら全ての式で下を採る)とする。
-----------------------------------------
任意の二数を a,b とすると,それらの2乗差は,
b^2 - a^2 = ( b-a )( b+a )
で,2乗差は,元数の和:( b+a )の
 ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄
元数差:( b-a )倍になっている!!!
 ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄
したがって,次の式が成立する。
<1>一つ違い( b = a±1 )の場合;
b^2 = a^2 ±( b+a ) …<1>
<2>二つ違い( b = a±2 )の場合;
b^2 = a^2 ± 2( b+a ) …<2>
<3>三つ違い( b = a±3 )の場合;
b^2 = a^2 ± 3( b+a ) …<3>
…………………………………………………
5の倍数( 5,10,15,…… )の2乗の暗算は
容易なので,5の倍数を a とすれば,
5の倍数以外のすべての整数 b の2乗
b^2 は上の<1~3>のどれかを
使って(特に b が二桁なら)簡単に
暗算できる。
…………………………………………………
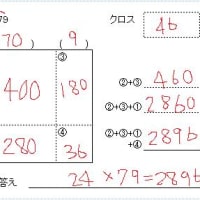
(例) a^2 =20×20=400 を基準に採り
下記の bn^2 を求める。
21×21=b1^2, 22×22=b2^2,
23×23=b3^2, 24×24=b4^2,
25×25=625, ‥‥‥‥‥‥
…………………………………………………
<1>を使って,
b1^2 = a^2 +( b1+a )
= 400 +(21+20)
= 441
<2>を使って,
b2^2 = a^2 + 2( b2+a )
= 400 + 2×(22+20)
= 484
<3>を使って,
b3^2 = a^2 + 3( b3+a )
= 400 + 3×(23+20)
= 529
…………………………………………………
b < a のときは,( b-a )<0 だから
<1~3>の ± の - 側を使う。
例えば,上の数値例で,b4=24 の
ときは,これに近い5の倍数として,
a=25 を選び
a^2 =25×25=625 を基準にする。
<1>を使って,
b4^2 = a^2 -( b4+a )
= 625 -(24+25) = 576
────────────────────────────
大変失礼しました。
垣間見みました。( 2019/07/07 )
7年前なので、もう管理されていないのかも
知れませんが,二桁数の2乗について,
超簡単!!!な暗算法を一言。
━・━・━・━・━・━・━・━・━・━・━・━・━・━
※1.以下では,Zの2乗を Z^2 等と表示する。
※2.複号[±)は同順(上なら全ての式で上を採り,
下なら全ての式で下を採る)とする。
-----------------------------------------
任意の二数を a,b とすると,それらの2乗差は,
b^2 - a^2 = ( b-a )( b+a )
で,2乗差は,元数の和:( b+a )の
 ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄
元数差:( b-a )倍になっている!!!
 ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄
したがって,次の式が成立する。
<1>一つ違い( b = a±1 )の場合;
b^2 = a^2 ±( b+a ) …<1>
<2>二つ違い( b = a±2 )の場合;
b^2 = a^2 ± 2( b+a ) …<2>
<3>三つ違い( b = a±3 )の場合;
b^2 = a^2 ± 3( b+a ) …<3>
…………………………………………………
5の倍数( 5,10,15,…… )の2乗の暗算は容易なので,
5の倍数を a とすれば,5の倍数以外のすべての整数
b の2乗 b^2 は上の<1~3>のどれかを使って
(特に b が二桁なら)簡単に暗算できる。
…………………………………………………
(例) a^2 =20×20=400 を基準に採り下記の bn^2
を求める。
21×21=b1^2, 22×22=b2^2, 23×23=b3^2,
24×24=b4^2, 25×25=625, ‥‥‥‥‥‥
…………………………………………………
<1>を使って,b1^2 = a^2 +( b1+a )
= 400 +(21+20) = 441
<2>を使って,b2^2 = a^2 + 2( b2+a )
= 400 + 2×(22+20) = 484
<3>を使って,b3^2 = a^2 + 3( b3+a ) ) = 400 + 3×(23+20) = 529
…………………………………………………
b < a のときは,( b-a )<0 だから
<1~3>の ± の - 側を使う。
例えば,上の数値例で,b4=24 のときは,
これに近い5の倍数として,a=25 を選び
a^2 =25×25=625 を基準にする。
<1>を使って,b4^2 = a^2 -( b4+a )
= 625 -(24+25) = 576
────────────────────────────