和算の終焉と西洋数学の台頭〜和算とその時代(終盤)

　前回では､江戸時代の和算が実用数学や娯楽として､広く当り前の様に普及してた様子を実例を示して紹介しました。
　そこで今日の最終回では､和算の終焉と西洋数学の台頭の流れについて述べたいと思います。
　和算は日本独自の数学である事のみが強調され､外国の数学の影響が殆ど無かったかの様に思われるが､中国からの影響があった事は容易に理解できる。だが､西洋数学(洋算)となると､それがどの程度導入されたのか？想像が付かないというのが実状だ。
　実際には､西洋数学が日本に流入するルートは開けていた。が､流入する内容は体系的なものではなく､その時々に必要とされてたものや偶然日本に齎されたものであり､現代社会の文化交流の形式とは大いに異なる。
　以下､前回と同じく｢和算の歴史｣から大まかに纏めます。

地図と暦学と西洋数学の導入

　例えば､17世紀中頃に幕府が国絵図を大名たちに命じて作らせていた際､地図作成の為の必要な知識を得る為に､オランダ人から数学(幾何学)を学ばせていた。だが､この西洋の幾何学の知識は断片的で､その後の和算書などに影響を見る事は出来ない。
　一方で､大々的に西洋数学が導入されたのは､江戸時代中頃の8代将軍吉宗(1716-45)の時期とされる。
　吉宗は”享保の改革”により様々な施策を打すが､財政面の事柄だけでなく､医療や科学技術･産業全般にも渡り､暦法改革もその1つでした。更に吉宗は､将軍就任直後から天文暦学の話題に関心を寄せていた。
　前回でも紹介した建部賢弘を重用し､暦学や地図に関する仕事を任せた。特に暦法に関しては､中国清王朝が西洋の天文学に基づき暦を作成してる事を知り､それに関連する本を輸入させ､建部と中根元圭(1662-1733)に研究を命じる。
　当時､洋書の中でもキリスト教宣教師の著作は輸入禁止措置が取られてたが､吉宗は西洋の暦法を知る為に､この禁輸措置を緩和する。
　即ち､キリスト教宣教師が書いた書物であっても､科学技術の著作であれば輸入してもよいとしたのだ。但し､対象となったのは中国語に翻訳された西洋の著作である。というのも､日本には未だに西欧の言語を自由に操れる人は殆ど皆無だったし､寧ろ幕府が警戒したのは中国語によるキリスト教の流布にあった。

　この緩和措置によってもたらされたのが､西洋の数学と暦学を纏めた梅文鼎(1633-1721)の｢暦算全書｣である。この本を建部と中根が研究し､今でいう三角関数の数表を取り込んだ。
　以後､日本の数学者たちはこの方面の研究も精力的に進め､数表の精密化に努力を傾ける。
　建部や中根に研究を進めさせる一方で､吉宗は幕府天文方のてこ入れも進めた。建部と中根は改暦に至る前に没したが､その後を受けた天文方のメンバーは望遠鏡などを用いた天文観測の準備を進める。
　山路主住(1704-73)と之徽(1729-78)親子は､幕府天文方に属した関流の和算家だが､吉宗に命ぜられオランダ人から天文暦学に関する知識を学ばさせていた。
　こうした吉宗の改暦事業だが､その成果を見る前に吉宗は没する。その没後すぐに作られたのが宝暦暦(ほうりゃくれき)だが､諸事情により前述の貞享暦(1684~1754)を僅かに補正したに留まり､施行されたのは僅か1754年~1798年までと､不完全な物で終わる。
　しかし､この宝暦暦を改訂する過程で､幕府天文方は吉宗が敷いた路線である西洋天文学の導入を更に進めた。つまり､天文学周辺にある西洋数学の知識を取り入れる事に繋がっていく。

　三角関数表の他に和算家が取り入れた西洋数学には､対数表や球面三角法がある。
　対数表は現在でも高校で教えられてるが､それと同じ物が江戸時代に輸入されていた。また､球面三角法とは天文学や地球規模で移動する様な航海術では必要になる算法で､球面上に描く三角形では平面の場合とは異なる公式が必要となる。
　更に､ヨーロッパの幾何学も18世紀以降､日本に入っている。例えば､仙台藩の和算家･戸板保佑(1708-84)は中国書｢数度衍｣に大きな影響を受けたが､それにはヨーロッパの幾何学の体系が中国語で記され､纏められてた。
　更に幕末になると､西洋数学導入の動きは加速し､天文暦学だけでなく様々な分野に応用される様になり､砲術･築城術･造船術など欧米の軍事技術の核をなす数学が紹介されていく。

　以上より､江戸時代における西洋数学の導入は､数学そのものより何らかの応用や実践を前提とし､それに必要な数学として取り入れられた物が殆どである。
　但し､ヨーロッパの最先端の数学(微積分や代数学)が体系的に取り込まれた訳ではない事に注意する必要がある。一方で､技術に必要な数学と､そして数学そのものを目的として研究する数学という2つの側面を共に認知し､本格的に取り込むのは､明治初期以降の事である。

和算の終焉

　江戸時代が終わり､明治以降になると日本は西欧に倣い､近代化をあらゆる方面で推進する。科学技術教育は特にその傾向が顕著で､当時の文部省は1872(明治5年)に初等教育に関する指針を策定し､学制として発布。翌年から小学校教育を開始した。
　中でも算数教育は､従来の和算ではなく､西欧の算数､即ち洋算によるもので､例外的に計算道具のそろばんだけは存続する事になる。以後､教育の現場から和算は姿を消す事になるが､学校が全国に設立され始めた当時､誰が洋算の知識を子供たちに教えていたのだろう。

　明治初期には数多くの算数の教科書や教師向けの解説書が刊行された。これらは非常に初等的な内容ばかりで､初等的な洋算を学べれば､算数を教える事は出来る。
　つまり､従来の和算を知ってる人達や和算家らが明治時代の小学校の教壇に立っていたのだ。勿論､それは過渡期の現象で､各地に師範学校が設立されると､近代的な教育を受けた教員たちによる洋算教育が徹底される事になるのは言うまでもない。
　こうして､和算家の社会的な役割も年を追う毎に小さくなっていく。
　また学術の方面でも､和算は近代化の過程で役割を終えていく。明治10年(1877)には､数理科学系の学会として国内では初の団体である東京数学会社(現･日本数学会)が有志により設立された。初期の会員構成を見ると､大多数は和算家または和算的な教育を幕末に受けた人たちで占められ､西洋数学を学んだ人や西洋数学を教える学者らは極少数だった。が､その構成も年を追う毎に西洋数学により教育を受けた世代に取って代わられ､明治の末年には和算は完全に過去の遺物と見なされる様になる。

　この様に､日本の算数や数学は､200年以上続いた和算の伝統をあっさり捨て去ってしまった様にも思える。当然､一部の和算家は洋算の浸透に対する露骨な不快感を表した。
　しかし､科学技術を根幹の部分で支える西洋数学を導入しようという時代の潮流に変化はなかった。つまり､幕末から明治初期に西洋数学をも学んだ和算家たちは､実学としての西洋数学の価値にいち早く気付いていた。
　社会に有用な実学としての数学との見方に従えば､彼らにとって役に立つ数学は和算であっても洋算であっても構わなかった。実際､洋算の導入を推進した人たちは和算をも学んでいた。故に､和算家が全て洋算に反対してた訳でもない。つまり､実学という視点で考えると､和算から洋算への転換は科学技術の点で見ても､必然的な動きだったとも言える。

　最後に､和算が近代になってからも地域教育に果たした役割があった事を紹介して終わりにする。東北地方や中部地方の一部には､私塾の形で昭和になるまで和算による数学教育が存続していたという。
　戦前の義務教育は小学校までで､学業を続けたくても様々な理由で断念せざるを得ない人たちが多数いた。そんな人たちの数学方面への知的関心を満たしてくれたのが､農村部で展開してた和算塾である。明治になってからも各地に算額が奉納されてるが､近代教育を補完する形で存続した和算教育という点で､興味深い実例である。
　以上､｢江戸の数学｣から長々とでした。

最後に〜世界に誇る日本の数学

　農村地区の日常生活を支えてた和算､そして知的好奇心を満たす役割も果たしていた和算。私達現代人はもう一度和算を振り返る事が必要な時期が必ず来るであろう。

　私はてっきり､江戸の数学(和算)は日本人が蘭学などを通じ､西洋から学んだものと思っていた。が､それは大きな間違いであった。
　最初は中国から簡単な算術を取り入れ､それを日本人の好みに合う様に､進化･発展させ､日本独自の和算として､ライプニッツやオイラーに匹敵する程の世界のトップレベルにまで押し上げた。
　今の日本人が聞いたら､”嘘だろ？”って声が届きそうだが､江戸時代の日本人は武士も役人も商人も農民も皆､数学が大好きだったのである。ま､それだけ江戸時代の日本は鎖国のお陰で､優雅でかつ平和だったのかもしれない。
　確かに､明治維新で西洋数学(洋算)を取り入れ､時代の流れに押し出される様にして和算は終わりを告げたが､既に和算という独自の数学があった。だからこそドイツの数学を輸入する際､いとも簡単に日本語に翻訳できたとも言える。

　一方で､日本の伝統的な数学である和算は長い歴史を持つが､現代数学つまり西洋数学の歴史は浅い。世界的名声を勝ち得た多くの日本人数学者の最初の一人は､明治時代の数学者で類対論の創始者である高木貞治氏である。
　順調にエリートコースを歩み､東京帝国大学を卒業し､ドイツへ留学した高木氏だが､ベルリン大のフロベニウス博士が”ああ日本からも来るのか？今に猿も来るだろう”と語ったとの噂が広まり､かなり警戒したが､それ程まではなかったという。
　ベルリンから数学世界の中心地であるゲッチンゲンに移り､少数学士の精鋭らを見て､高木氏は衝撃を覚えた。
　”私は25にもなるのに・・日本の数学は50年遅れている”と感じたらしい。が､1年半ほどゲッチンゲンに留まっていると”50年の遅れが解消した気分になった”とも語っている。
　そんな高木氏だが､ヒルベルトに弟子入りする際､”君は整数論をやるのか？”と驚かされたという。当時､代数的整数論というのはゲッチンゲン以外では世界中で見ても誰もやる人はいなかったらしい。
　こういう所にも､日本伝統の数学である和算の影響を色濃く受け継いでいるのである。

　確かに､和算の基礎があったから､高木氏を含め､数学のノーベル賞ともいわれるフィールズ賞を日本人は3人も受賞している。国別の受賞者数では､天才数学者を数多く生み出した米仏ロ英に次ぐ5位で､日本は世界を代表する数学大国であり､その原点が和算とも言える。

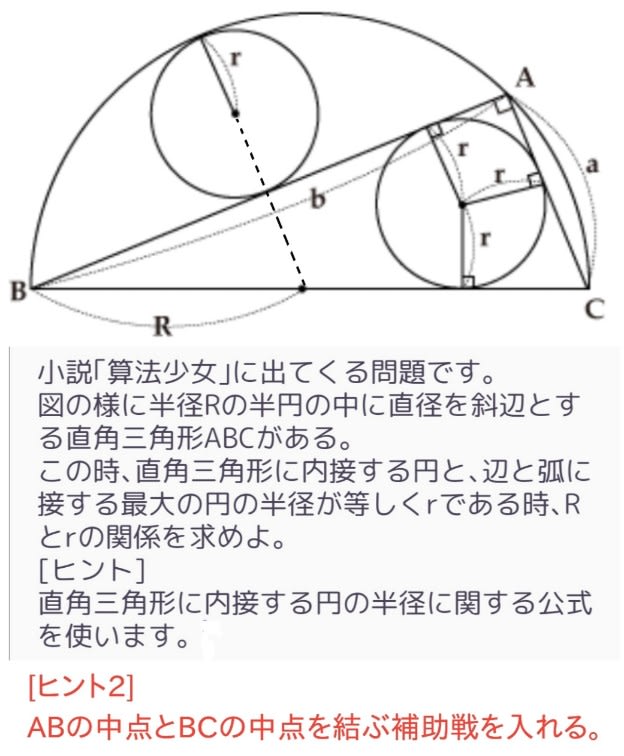
　算額には”容術”と呼ばれる､ある図形に別の図形を幾つも内接させる問題がよく取り上げられていた。江戸時代の庶民たちは､日常の娯楽として､こうした幾何学の問題を解いてたのであろう。
　上図に､問題を出しておいたが､現代人も負けずに解いてほしいもんだ。