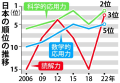
日本人の学力低下が叫ばれて久しいが、本当に日本の子供たちは頭が悪いのだろうか? PISA2022(世界中学生学力ランク)によると、日本は数学力(5位)、読解力(3位)、科学活用力(2位)と、3分野全てにおいて世界トップレベルとなった(上図参照)。 2022年は世界81カ国の69万人が参加し、15歳児を対象に調査を実施した。因みに、3部門とも1位はシンガポールだ。 では、高校生を対象にした数学力は . . . 本文を読む
1等の当選確率は”2000万分の1”という限りなくゼロの数字だが、我ら大衆はまるで当選したかの様な期待を抱き、宝くじを買ってしまう。 一方で、”夢を買うには安すぎる”とも言えるが、もし、AIの様に機械的で合理的な思考をもってれば、宝くじを買う人はいなくなる筈だ。 因みに、2018年の年末ジャンボ宝くじの1等当選確率は、0.00000005%だった。 . . . 本文を読む
「テイラー展開とその定理」では、”ローラン展開は特異点(正則でない点)の周りで展開する”と言いましたが、当然ながら”領域内は正則である”との条件が付く。これは、領域内に極や特異点があると展開できないからです。但し、以下でも述べるが、正則関数とは(領域内)全ての点で何回でも微分可能な複素関数の事で、微分回数が制限される実関数とは性格が異なる。 つまり . . . 本文を読む
某大学の医学生が”ローラン展開とかイマイチよく分からん”と嘆いてたのを思い出す。 複素関数でよく登場するテイラー展開とローラン展開だが、どちらも複素関数のべき級数展開である。そして、極とか特異点とかの専門用語もしばし登場する。 これらは複素関数を積分したり、複素解析において非常に便利なツールと言える。 私も一応は数学科の出なので、必要最低限の理解はあったつもりだが、時間が . . . 本文を読む
映画「アルキメデスの大戦」では、主人公で”100年に1度の数学の天才”と呼ばれる櫂直(かいただし)が、制約された条件と時間の中で戦艦大和の建造費を算出する。 そこで彼が思いついたのが、鉄の総量から建造費を算出するもので、”鉄が少ない部分は構造が複雑でパーツも多く、建造費が高く付き、鉄が多い所は構造がシンプルで安く付く”というシンプルな数学的(解析) . . . 本文を読む
1昨年末以来の”バーゼル問題”ですが、間が空きすぎたので、簡単におさらいをします。 前回「その7」では、無限解析によるバーゼル問題の完璧な証明を紹介しました。 1734年の最初の証明には(微かな事でしたが)幾つかの問題がありました。だが、その10年後の「無限解析入門」(出版は1748年)では無限解析を用いてほぼ完璧な証明を与えています。 オイラーの完全なる”バ . . . 本文を読む
ノイマンは”君はあれを使ったのか?”とナッシュJrに問うと、彼は”ハイ、使いました”と言ったそうだ。 その”あれ”こそが”連続な関数でも不動点は存在する”という角谷静夫氏の「ブラウワー不動点定理」でした。 つまり、かのフォン・ノイマンでさえゲーム理論には使えなかった角谷の定理を、ナッシュは見事に使っ . . . 本文を読む
NHKBSでは「素数の魔力に囚われた人々」という番組が流れてた。これは「リーマン予想・天才たちの150年の闘い」というタイトルで2009年に放送されてたものだ。 オイラーから”素数の謎”のバトンを譲り受けたガウス少年は、素数のパターンを自然対数logに見出した。つまり、素数の出現確率が自然対数の逆数に一致すると予想した。事実、ガウスの素数定理は”π(x) . . . 本文を読む
昨年4月以来の望月教授の宇宙際タイヒミュラー理論ですが、「前回」とは異なり、今回は小難しい話はやめにして、誰もが知ってる”掛け算や足し算から宇宙理論を眺めて”みたいと思います。 IUT(宇宙際タイヒミュラー)理論とは、望月博士が約20年かけて築いた数学の理論で、”足し算やかけ算をする世界(=宇宙)を縦横無尽につなげ(=際)、数を自在に行き来させる(復元=タイヒ . . . 本文を読む
”悲しすぎた”東京五輪も”笑えない”大阪万博も、予め矛盾や問題が起こりそうな要素を徹底的に排除し、最悪を想定する。更に条件を厳しく且つキメ細かく設定し、徹底したリスク管理の下で万博プロジェクトを推し進めてたら、もっと効率のいい”箱モノ”が出来たであろうと思わないでもない。 それに、昨今のプロジェクトリーダーらが数学的思考に恵 . . . 本文を読む