この只(ただ)ブログには，字数制限があるので，前記事で一応まとめののようなことを書いたが，内容はPart Iを走り読みした感じのことだったので，Part IIの座標の話から書いていこうと思う．
座標系が，例えば，直交座標でも斜交座標でも極座標でも，反転変換と鏡映とか，円の反転変換とか，アポロニウスの円と反転変換，あるいは平行と反転変換の組み合わせと対応しているように見える．また，正，0, 負が反転変換の範囲を延長して考えられているようにも見える．Newton以前の，フェルマーやデカルトが，座標を0と正の場合に限ったのも，反転変換の延長で見ようとしていたということだろうか．Newtonが，ある意味，そういう対応を離陸させたということだろうか．そこにすでに非ユークリッド幾何の萌芽がみられ，ニュートンはそれを絶対空間や絶対時間として相対化していたというようなことになるのだろうか．別の箇所には，「平行線の一意性が重大な役割をはたすアフィン幾何学」の命題が「ミンコフスキーの時空幾何学にも成り立つということがわかって，アフィン幾何学の重要性が再認識された」とも書いてあるので，あるいは，「群」の概念等がともに生い育ってきたのかもしれない．それともう一つ，コクセターの確率論への寄与という点も重要であるらしいが (参考:『岩波数学辞典』)，おいおい読み解いていかなければならない，はずではある．
その前に，ちょっと補足しておく方がいいと思われるものを書いておく．
『原論』第３巻の命題36(III.36)から，この命題は，要するに，辺CDと辺ADで囲まれた長方形の面積はBD=DTを一辺とする正方形の面積に等しいということだから，点Dを中心とする，半径DBの円を反転円として，点Aは，点Cの反転像であるということと同じだから，命題は，そういうことが証明できるという主張だから，
DC × DA = DB^2 = DE × DO．
(6.21 与えられた点Pの反転像は，Pを通り反転円に直交する2つの円の第2の交点Qになっている．)
円Oは反転円，点Pを通る2つの直交円あるいはその中心をO_1, O_2とする．三角形OAO_1, OBO_2は直角三角形である．
Oを通らない円Cは，Dを中心とする円に反転される．ここで，
p=q^2=OP×OQ, k^2=OP×OP', CQとDP'は平行．同心円による2つの反転の積である一つの拡大はO(μ), μ=(k/q)^2=k^2/pである．
アポロニオスの円は，2定点A, A'からの距離の比が一定 1:μ である点P，つまり
A'P = μAP
を満たす点Pの軌跡は，μ=1のときは，AA'の垂直二等分線であり，μが1に等しくないときは，直線AA'と角APA'の二等分線のまじわりA_1と，角A'PEの二等分線のまじわりA_2の3点を通る円A_1PA_2である．そのような円のことである．
アポロニオスの円を反転円として，AとA'は互いの反転像となっている．
では，座標について，
直交座標 (orthogonal coordinates, Cartesian coordinates)
斜交座標(oblique coordinates)
基本的なことで，線分の内分と外分については，
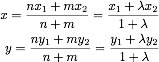
極座標(polar coodinates)
極座標では，Oを極，半直線Oxを原線とか始線という. rを動径, θを偏角といい，この一組の数r, θをPの極座標という．点Pの極座標をP(r, θ)という記号で表す．θは始線からOPへ，反時計回りにとる．gは，OとPを通る有向直線である.
Part IIは，「解析幾何学」という言葉で始まっている．以下，『岩波数学辞典』から，解析幾何学(analytic geometry)とは，幾何学の問題を座標によって数の間の問題に帰着して，代数的に処理する方法である. しかし，すべての幾何学の問題に対して，この処方が最適とは限らない．座標を用いないで図形を直接考察する立場の幾何学を総合幾何学(synthetic geometry)または純粋幾何学(pure geometry)という．
幾何学の分類では，「非ユークリッド幾何学はユークリッド幾何学が無矛盾である限り無矛盾であり，両者の違いは異なる計量の基準によることが明確となった」などから，次の分類が基本のようである.
放物幾何学(parabolic geometry) --- ユークリッド幾何学
楕円幾何学(elliptic geometry) --- リーマンの非ユークリッド幾何学．
双曲幾何学(hyperbolic geometry) --- Lobachevskiiの非ユークリッド幾何学．LobachevskiiやBolyaiらの「絶対幾何学」．
クラインのエルランゲン目録の立場，つまり，群の立場(空間Sの変換群Gの作用で不変なSの図形の性質の研究)から，例えば，運動群(合同変換)がユークリッド幾何学を定めるというような立場から，射影幾何学，アフィン幾何学，共形幾何学，(非)ユークリッド幾何学などを統一的に扱える．また，ワイル(Weyl)やカルタン(Cartan)は，多様体の上の幾何構造を考察し，カルタンは，幾何構造を不変に保つリー群を構造群とする主束(principal bundle)上に接続の概念を導入し，RiemannとKleinの思想を結びつけた，とある．
初歩的に読めば，同値関係を定めて，それによる同値類の構造を，位相変換の作用で不変に保つ対象を作っている感じである. 分割数などにも関係するのだろう．オイラーやラマヌジャンのテータ関数という感じなのだろうか．
肝心なことを書き忘れていたが，「解析幾何学というのは，n次元の空間の点を，座標というn個の順序のついた数の組みで表す方法であるといってよい」( 「8.1 デカルト座標」の冒頭，コクセター『幾何学入門』)
(8章3節の問題1)
最初の式は円の方程式である. Pは任意だから，結果を，x_1, y_1をx, yで代用すればいい．
(8章3節の問題2) 点(k/μ, 0), (μk, 0)からの距離の比が1:μに等しい点(x, y)の軌跡(アポロニオスの円)を求めよ．
原点(極)Oを中心として，半径kの円を反転円として，点P(r, θ)の反転像Q(q, θ)を求める．
最後の式は，極座標P(r, θ)，Q(k^2/r, θ)を，直交座標P(x, y), Q(x', y')で見れば，ということである．円x^2 + y^2=k^2は，極方程
で書けば，θに関わらないから，r=kである．煩わしくなるので，OP=r はOP=pとでもした方が見やすい．次と比べてみるのも良いのかもしれない．
この場合は，中心Cの円の極方程式は，r=2kcosθである．OAは一定，Pが円周上のどこにあっても角OPAは直角．rは動径, θは偏角のことだから．pがOの位置にあるときは，r=0で極にあたる点，PがAの位置にあるときは線分OAだが，極方程式は成り立つから．
座標x, yについて，1次方程式 Ax + By + C = 0を満たすグラフは直線を表し，2次方程式
を満たすグラフは，2次曲線(quadric curve)または円錐曲線(conic section)と呼ばれる曲線である．円錐曲線は楕円(円を含む)，放物線，双曲線の3つであるが，点や一対の直線(交わる，平行な，重なる)も含める．3次曲線(デカルトの葉形など)，4次曲線(パスカルの蝸牛形，レムニスケートなど)なども考えられる．
円錐曲線は，焦点(focus)と呼ばれる定点Fからの距離FPと，準線(directrix)と呼ばれる定直線l(Lの小文字)からの距離PQの比が一定εであるような点Pの軌跡である．定数εは離心率(eccentricity)と呼ばれ，ε=1のとき放物線(parabola)，ε＜1のとき楕円(ellipse)，ε＞1のとき双曲線(hyperbola)と呼ばれる円錐曲線である．焦点を通り準線に平行な線分は通経(latus rectum)と呼ばれる．
円錐曲線の一般的な方程式を
と書けば，
は，座標変換に対して不変である．特にΔを2次曲線の判別式という．δ=0のときは無心2次曲線(放物線や平行な2直線)，δ>0(楕円，一つの実点を共有する虚２直線), δ<0(双曲線，交わる2直線)のときは有心2次曲線．(『基礎数学ハンドブック』)
楕円の場合は，
というような図解である．楕円はFP +F'P=一定(2a)な点Pの軌跡として定義されるから(点Pが点Aの位置にあるときを考えれば2aであることがわかる. F'P=F'A，FP=FA=BF'となるから)，c=εaと置いて，つまり，F(c,0), F'(-c,0)として，計算して，b^2=a^2 - c^2とすれば，標準形が得られる．
(8章5節の問題11) 円r=aに関して，直角双曲線r^2=a^2sec(2θ)は，ベルヌーイのレムニスケートr^2=a^2cos(2θ)に反転される．
OA=a, 双曲線上の点Mは，円Oを反転円として，OM上の点Pと互いの反転像となっている．点Pの軌跡がレムニスケートになるということなのだろう．原点Oは反転の特異点だから，無限遠点に対応していると考えなければならないと思うが．
放物線では，楕円ではと考えると，線分(X軸上の)を行ったり来たりとか，楕円というのか，楕円とは定義からして違うが(カッシーニの)卵形ぽかったり(下図Eの軌道)，図形ソフトは，関係を保ちながら点を動かせるので，動かしてみると，見た感じそんな動きである．対称性と双対性が幹細胞を増殖させる感じなのだろうか．そういう変化を期待したくなる．例えば，ケプラーの第二法則とか．
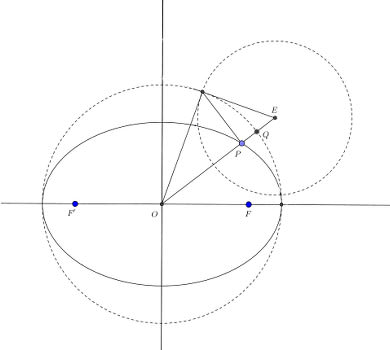
点EがY軸と重なる点とか長軸の端とか，５点を通る２次曲線を動かすと，楕円だったり双曲線になったりするから，卵形(oval)も楕円に歪めないと，彗星軌道に乗ってしまう時も生じそうなので，楕円軌道が安定的に維持されるメカニズムにも関連するのだろう．
さすがに，一挙に飛ばして，微分幾何学に行きたい．曲線の接線や法線や曲率を，積分の逆関数を求めて，そのべき級数展開の1次近似や2次近似として求めるとか，超幾何級数だの楕円関数だの，本格的な数学の香りがするが，微分幾何学は，「幾何学的構造を備えた微分可能多様体の研究」なので，非線形偏微分方程式とか確率微分方程式とか繋がりが深いらしいが，そういう高度なことは置いておいて，初歩的な部分からつかめればいいかなという方針で読んでみたい．「「読む」の試み(3)---微分幾何学」と行きたいところである．
