「コクセター「幾何学入門」を読む」の試み(4)

Coxeter『幾何学入門』上，下，約850ページの数学本の数多い項目を当たるのは，さすがに眠たくなるが，およそ最も基本的で初歩的な項目は，一応たどったことにしておいて，加群だの線形空間だの，微積分だのの基本的な事柄をまとめておく方が，再読するにも都合がいいだろうということで，メモ書きしていきたいと思う．こういう分野は，教科書や参考書の要約ノートをとるくらいしかまとめようがないのだが，地味な手間も必要なのが，理系の科目というものなのだろうと，慮ってみる．

ここまで参考にしながら拾い読みした文献や関連の強そうな文献で手持ちののは，

『基礎数学ハンドブック』森北出版

『代数学・幾何学精説』培風館

『曲線と曲面の微分幾何』裳華房

『解析概論』岩波書店

『空間と時間の数学』岩波新書

『現代数学概説I, II』岩波書店

『自然科学者のための数学概論』岩波書店

「数学辞典」岩波書店

ニュートン『光学』岩波文庫など岩波文庫や新書，ちくま学芸文庫などの理系の文庫本や新書，『アインシュタイン選集I, II』とか物理関係の本もいくらか買いためてあるが，理系でないので，細かい事情は知らないから，古典的名著とか必読というような謳い文句に促されて買ったものがほとんどである．うん１０年前の本が多いのだが，趣味で買いためたものだから，紙束にしたままにもいかないので，使えるものは使うという方針でまとめたいと思う．これらの参考書は，専門家の書いた教科書あるいは啓蒙書だが，説明が丁寧なところが素人の理解には助かるのである．しかし，自分でまとめようとしたりすると難解きわまりないものになるから不思議である．

 ユークリッド幾何学から，圏と関手(Category and functor)のように，対象領域を拡大して，写像の拡張概念(汎射)のようなものを使って，同値類を定めて，いろいろな性質を見ていくような理論を導き出すような構成を目的としているのかどうか，という問題も生じると思うが，Weylの「群論と量子力学」も「合成」を基本として理論を組み立てると最初の方に述べているのだから，趣旨が通じている感である．気になることの一つは，数論のような対象が，そのような理論の拡張の上に建てられる様子が，実際どういう感じで成されるのかということである.

「群の表現理論とともに，量子力学の演算の数学的な場(field)は，多次元アフィン空間あるいはユニタリー空間である. 公理的な方法が，そのような空間の幾何学を展開するのに，最も適切であることは間違いないが，見通しを良くするために，まず，純粋に代数的な方法で始めることにする．」(『群論と量子力学』)

「テンソル解析を展開するのに純代数的方法は，その簡明さと理解しやすさという点で優れている．これに対して幾何学的な方法は直感的という利点をもつ．」(パウリ『相対性理論(上)』)

「我々が乗法を加法に帰せしめることを断念するかわりに，これらの公理(ベクトルの公理)は我々に幾何学の論理的建設から把え難い連続性を全く追放する能力を与える．」(ワイル『時間・空間・物質』)

 ユークリッド幾何学が，実数の連続性を，公理として要請する体系だということだろうか．算数でいえば，2×3=2+2+2=(1+1)+(1+1)+(1+1)=6というようには，いつも同じように考えることはできないということだろうか.

ベクトル空間は Fを(係数)体とするF-加群(体Fを台集合とする，Fの上の加群)である．一般に，Aを単位1をもつ環(単位環)とする．Mを加群とする．α∈A, x∈Mに対して，αx∈M(またはxα∈M)が定義されて

が成り立つとき，MをA-(左)加群という(xα∈MのときはA-(右)加群)．A-加群で，Aが体Fのとき，F-加群をFの上のベクトル空間という．直感的には，「点Pから点Qへ線分が引けたとせよ．その線分の長さと，PからQへという方向を一組にしたもの，それをベクトルということにしよう」という感じだろうか．

Weylの公理系ということで，

[ベクトルの公理]

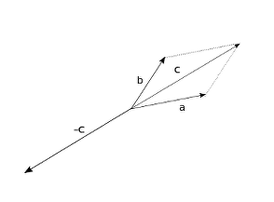
n次元線形空間R^nのベクトルvec{x}は，n個の順序付けられた数の組みである．ベクトル解析は，そのような順序付けられた組みの計算法である．基本となる2つのベクトル演算は，ベクトルxにある数aを乗じるというものと，2つのベクトルx, yの加法である．

という表記を導入すれば，これら2つの演算は，次の等式で定められる．

これらの演算が，次の公理に従うとき，R^nはベクトル空間であるという．

 『空間と時間の数学』(岩波新書)では，III(計量の公理)，IV(次元公理), V(アフィン公理)と続くのだが，IVのベクトル空間Vの次元は，Vのn個のベクトルが一次独立で，どのようなn+1個のベクトルも一次従属となるとき，あるいはベクトル空間Vがベクトルを元にもつ列(vec(a1) vec(a2) ... vec(am))(ベクトル系)のサイズ(ベクトル列の長さm)が最小でも$n$のベクトル系で生成されるとき，ベクトル空間の次元は$n$であるという公理，IIIは，ベクトルの内積の性質を一般的に見て，計量を定める公理として採用して，計量ベクトル空間を定義するもの．Vは点の集合である空間Eとベクトル空間Vを結びつける役割をすると考えられる公理で，アフィン空間を定める公理である．

[双対ベクトル空間]

任意のベクトルxの関数L(x)が，

　(1)

という形に表されるとき，線形形式(一次形式)という．アフィン幾何学においては，この概念は不変であり，

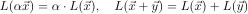
という関数特性で定義される． 式(1)がこれらの性質を満たすことは明らかである．また，逆に，座標系e_iを導入して

とおけば，

が従う．

任意のベクトルxの成分x_iを(座標の)変換法則にしたがって変換して，座標を取り替えたときには，線形形式は

となるが，もともとのα_iに対応するα'_iは，

という等式で結びつけられている．線形形式の係数α_iは，変数x_iに対して，反傾的に(contragrediently)変換されるという．

しかしながら，α_iを定数，x_iを変数と考える必要はない．α_iのすべてが0というわけではないとき，方程式L(x)=0は一つの''平面''を定める．すなわち，(n-1)次元部分空間である．その成分がこの方程式を満たすならば，ベクトルxはその平面に含まれるという．また一方で，すべての平面の方程式は、非ゼロベクトルx^0を与えることによって求められる．x_i=x_i^0はそのとき定数で，α_iは変数である．なので，2つの組

を並行的に考えるのが最も適当である．

そこで，空間Rに加えて，第2のn次元ベクトル空間, 双対空間Pを導入しよう．Pのベクトルξの成分とRのベクトル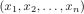から，内積あるいはスカラー積

　(2)

を作ることができる．この積は，明らかに，不変的な特徴を持っている．Rがx_iの変換によって新しい座標系に参照されるとき，双対空間Pの変数ξ_iは，反傾変換を被る．この双対空間は，実は，反傾変換を各一対一変換に結びつけるために導入されたのだった．くり返して述べれば，二つの線形反転変換

x = A x',  ξ= Aξ'　(3)

は， (2)を不変に保つならば，

 (4)

ならば，互いに反傾である．

RのベクトルxとPのベクトルξは，それらの積(2)が0となるならば，対合(involution)の関係であるといわれる．Rの射線はPの平面を定める．すなわち，与えられた射線と対合の関係にあるベクトルからつくられる平面であり，その逆も成り立つ．双対性は相反関係(reciprocal relationship)である．

(以上，『群論と量子力学』から)

( O1×O2×...×On)×RからRへの対応で多重線形関係を保つようなものを考えることが，双対空間とか転置空間と呼ばれるものをとる目的であるということなのだろう．同型射を定めるという表現だろうか．類(型)射を定めるという感じにも思えたりする．これは，私の単なる言葉遊びで，数学的に正確な話ではないが．

続けて訳すと，

 

[アフィン・ベクトルに関する基本的な事柄について，簡単にメモ(『基礎数学ハンドブック』から)]

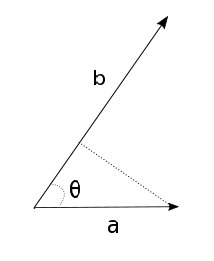
 アフィン成分表示でのベクトルa, bの内積や外積は，内積に関する分配則，外積に関する分配則が成り立つことから，計算できる．

 

 

 

「コクセター「幾何学入門」を読む」の試み

定規は，プラスチックや竹製のものでも，足で踏んづけてポッキと割ってしまったり，背なかを掻くのに使ったりするが，定規を当てて直線を引くという本来の使い方をしても，線が段になって，もう一度引こうとすると，途中から二重の線になったり，コンパスも，円の始点と終点が合わず，螺旋を描く道具ではないかと錯覚したりすることが多いのだが，そういうことで，私は，最近まで，幾何図形らしい図を描くにはフリーハンドが一番ではないかと悟ることにしてきた．

定規で直線を描くといっても，綺麗な直線を引くには，鉛筆をひらぺったく削って，外側から定規に当てるとか，結構気を使わなければならない．コンパスも，ネジが緩んでないかとか，中心が途中でずれてないかとか，こちらも結構気を使うものである．最近は，フリーの作図ソフトもあるので，そういうことはどうでもいいのかもしれないが．作図ソフトでは，円の中心を描く様に設定する必要もあるとか，コンパスで円を描いた方が早いという感じもないわけではない．

幾何図形といえば，中学校生の頃は，どう補助線を入れるかとか，図形の問題では教わるものだったが，次第に，初等的な図形は，もやっとしたシミの様なものになり，図形そのものがあってもなくても，どうでもいい様なものとなってしまったが，文庫や新書などの教養書で，三角形だの円だの長方形だのという図形に出会うと，不思議と気分が和むものである．

Harold Scott MacDonald Coxeter(1907-2003)の``INTRODUCTION TO GEOMETRY", Second Editionの銀林浩訳(ちくま学芸文庫)を読むを試みると題したのだが，とりあえず，目を引くところを拾い読みしてみる．

「任意の三角形の内角の隣り合った3等分線の交点は，正三角形を作る」というモーリーの定理も，『原論』の中の，「与えられた直線角を二等分すること」という命題が基本のようであるが，この命題から，円の半径と円の半径の逆数 (曲率）の間の双対的な関係式が得られるというのは，やはり面白く感じるものだろう．『幾何学入門』の説明の所では，

α + β + γ = 120, α=β=γ=40

とおけば一番簡単そうだが．「任意の三角形」が正三角形(等辺三角形)になるから．また，任意の正三角形をABCとすれば，角BIC=120=90 + A/2となる点Iは，三等分線の交点で作られる正三角形PQRの内心(=外心=垂心=重心)となるから．当然，全ての正三角形は相似である．ある三角形をその三角形自身と比較すれば合同でもある．しかし，説明で使われるのは，任意の三角形の頂角の三等分線から作られた正三角形の頂点である(ユークリッド風に言えば，「BICとなる点Iを取ったとせよ」で点IはPに取られていて，点Pは三角形BP'Cの内心になっていることが証明の鍵になっている)．リーマン面（リーマン幾何）だろうか．

この図は，こんな感じだということを示しているだけで，フリーハンド(手書き)よりももっと正確な図ではない．

垂心(垂線の交点)Hは，外心(垂直２等分線の交点)Oと重心(中線の交点)Gを結ぶオイラー線上にあるという関係は，

OA'とAHは平行で，三角形OA'Gと三角形HAGが相似(相似比1:2)な三角形であることから証明される．

角の三等分線を定規とコンパスだけで引くことは，ギリシャの三大作図不可能問題

1) 角の三等分問題　------ 与えられた角を三等分すること

2) 立方体倍積問題 ------ 与えられた立方体の体積の2倍に等しい立方体を作ること

3) 円積問題 ------ 与えられた円と等しい面積を持つ正方形を作ること

から，不可能だが(いずれも不可能であることは証明されている)，分度器使ったら簡単じゃないかと思ったのだが，しかし1/3=0.333333......で，分度器のメモリを細くするにも限度もあるし，きっちり正確でなくて良ければ，実際上は，ほぼ三等分に見えるだろうということで妥協するしかない(角の二等分線は作図できるのだが)．

 

九点円の定理 --- 三角形の3辺の中点，垂心と3頂点を結ぶ線分の中点，3本の高さの足は同一円上にある --- の図で，点Oは外心，点Hは垂心，点Nは線分OHの中点で，問題の９つの点を通る円の中心である．証明は，三角形の二つの辺の中点を結ぶ線分は第３辺に平行でその半分に等しいという中点連結定理と円周角不変の定理(特に弦が直径のときは直角)，から，問題の9つの点が同一円周上にあることが証明される．

 

 

５つの点を頂点とする多角形の頂点から線分を切り取ることなく(凹になった部分をまたぐことなく)線分を引ける範囲の重なる部分を色付けすれば，

最大で凸五角形となるというのも考慮に値するかもしれない．最小は三角形(点や線分を除けば)．理想化して言えば，円に限りなく近づける感じである．万華鏡(kaleidoscope)や星型多角形は、理想化の一つなのだろう．円分方程式もそうなのだろう．線形計画法とか最適解問題とか経済数学などへの応用も，ある意味，理想化の一つなのだろう．

 「この（鏡映）対称性を利用する方法は近道にすぎないのだということはいっておかなければならい．三角形の合同を使うまわりくどいいいまわしで，このような対称による証明をいっさい消去することさえできるのである」．三角形の各辺の長さをa,b,cとおけば，s=(a+b+c)/2とおくとか，角度α，β，γを適当にとってα+β+γ=90度になるとか，鏡映と合同を重力場になぞらえて考えてみるとか，ある種のon-offスイッチが入るような感じがする．それが，＜順序＞とか＜間>という原始的概念や関係になるのだろうか．

「2つの円周が交わることは，どうやって保証されるのか?」という問いも，「線分は，その両端の間に一様に横たわるものである」というユークリッドの定義によるとすることができるかもしれない．ユークリッドの『原論』の第I巻の「命題1　与えらえた有限な直線(線分)の上に等辺三角形(正三角形)を作ること」で，与えられた線分をABとして，点Aと点Bを中心として，半径ABの円を２つ描けば，これらの円がまじわる点CからAとBに線分を引けば，三角形ABCは正三角形になるとして作図されるが，「2つの円周が交わることは，どうやって保証されるのだろう?」と問うて，ユークリッドの『原論』にも細かい点での変更の必要が認められると言っているわけだが，『幾何学入門』の「12.1 ユークリッドから抽出された2つの幾何学」，つまり絶対幾何学とアフィン幾何学，の双方に属する核心的概念である順序あるいは＜＜間＞＞という概念を，ユークリッドは，「線分は，その両端の間に一様に横たわるものである」という有名な定義の中に使っている，あるいは，『原論』第I巻の「定義4 直線とは，その上にある点について，一様に横たわる線である」及び「公準2 有限直線を連続して一直線に延長すること」の中に使っていると言えるのではなかろうか．「２つの円周が交わること」はそれによって保証されていると言えるのではないかという趣旨である．

「公準4 すべての直角は互いに等しいこと」も同趣旨のような感じがする．

次は，タイル張りのデザインに使えるはずである．コンパスだけでも正六角形の頂点を描けるし，線分の2等分点でも３等分点でもn等分線点でも描ける．

 「与えられた線分」をn等分するには，反転変換というものが必要であるが，「n等分された線分」を引くのは簡単である．

中心をOとする半径kの円が与えられているとする．この円を反転円とする，中心点O以外の任意の点Pの反転像P'は，半直線OP上の

OP×OP'=k^2

を満たす点のことである．図で，点TはOPのPにおける垂線と円周の交点，TP'は反転円の接線となっている．

色づけした部分は，正方形だが，勝手につけたものである．四辺形どうしで重ならない部分は相似ではあるが．

次の図は，線分OAを5等分したものである．線分OAを5倍したところにある点P'を，半径OAの反転円によってPを反転させた像とみなしたものである．「解答」にある指示はこういうことだろうということで描いてみた．

OP' = 5OA,  OA : OP' =OP : OAだから， OP×OP' = OA^2,したがってOP= OA/5.

作図された図形を，勝手気ままに眺めていると，図形を作図するということが，「素数の密度」に妙に親和する感じを受けることがある．素数は無限にあるということが，幾何図形の作図にまとまりや秩序を与えるものになっているのだろうか．

ところで，ユークリッド(Euclid)とかエウクレイデスと呼ばれる人物は，詳しいことはほとんど知られていないが，BC300年頃アレクサンドリアで活躍し，エウドクソス，テアイトス，ピタゴラス学派などの業績を集大成し，厳密な論証にまで高めた『(幾何学)原論』13巻を著したが，『原論』すなわち``Stoicheia"(ストイケイア)は，もともとアルファベットの字母を意味する言葉で，『原論』を表す英語のElementsには，古代哲学で自然の物体の基本要素とされる四大，すなわち，火(fire)，空気(air)，水(water)，土(earth)の意味もある．古代ギリシャの自然観が現代の自然観(科学)のようなものでもないことや，古代ギリシャの文献が，アラビアにわたって保存，編集されたというような歴史的な経緯も難しい事情を作っているらしい．Euclidは他にも多くの著作を残したそうであるが，『原論』は主著にあたる(参照:世界の名著『ギリシャの科学』)．

 読んだところまでの流れからいえば，ユークリッド幾何学を，鏡映と反転というような変換が，例えば，アポロニウスの円の問題，座標や，円錐曲線等を媒介して，さらに微分幾何へと誘っている感じはあるが，ユークリッド幾何学を，線形場あるいはベクトル空間の構成場のように捉えている感じもある．そういうところが，コクセターが現代のユークリッドと称される所以のだろうか．反転を行って点PをP'に移す変換では，Pを反転円の円周に取れば，Pはその変換で不動点となる(P'はP自身となり，Pは反転で動かないから)．反転円の中心は特異点である．あるいは，反転という変換の作図も，2つの直角三角形，△OTPと△OP'Tが相似であることから保証されるわけだから，相似という関係が合同に媒変数表示を与えるとか，極限の概念を含んでいるとか，『幾何学入門』の目次に従うような構成になるということを，におわせている感じである．端折ってしまって，話が漠然とした感じになるが，そういう観点から読み直して，幾何学らしい，数学らしい話にしていく手始めの作業である．

とはいえ，さらに，平坦とかリーマン接続とか，相対性理論とか，あるいは超弦理論とか深く関わる問題に発展するらしい(参考:『岩波数学辞典』)．平行と離散の関係(格子)を，{0,1}時空間格子と考えれば，エルゴード格子になるのじゃなかろうかとか，「読む」を試みるのも，どこまでまとめればいいか分からなくなるくらいである．

「読む」を試みて，まとめるには，「はじめに」とか「まえがき」とか「序文」とか書かないといけないが，大方，その時点で躓くものである．

 

 

 

古典と現代------歴史と論理の相互規定について考える

 球座標　

　　

　とおけば，だから，

　　　，

　から，

         .

　

これは，デカルト座標系O-XYZの座標(x, y, z)と球座標(r, θ, φ)の間の関係であるが，(科学理論の)歴史と論理の間の，また経験と論理の間の相互規定を考える材料の一つであるということであるが，物理の古典理論の形成と，現代の理論の間の相互的な関係，古典理論の進展から生まれた量子論や相対論が，また，古典理論を基礎づけるという関係は，物理に限らず，生命現象や社会現象の解明を目指す理論にも共通するものなのだろう．古典理論の意義は，懐古的な安住とは程遠い，現在や未来との緊張関係であるということなのだろうが，同時にまた，経験的な確かさを与えるものでもあるということだろうと思う．

ユークリッドの数論も土地の面積を測るという実用的な問題と無関係だったのかとか，複素数も，x^2 + 1 = 0に解を持たせるために，虚数を導入したのは，カルダノで，オイラーがそれを正当な数として認めて虚数単位記号iを用い活用し， ガウスが複素数という名の名付け親で，複素平面もガウスの考案．現在では，実数全体の集合Rを複素数全体の集合Cの部分体として，a + biは単なる記号の形式的な表示から，体Cにおける演算とみなされることになる．というような，数学上の経緯も類似性を感じさせる．当然，コンピュータで数をどう扱うかという問題とも関連しているはずである．intとかdoubleとかfloatとか．floatや行列演算用のチップというのかモジュールというのかは別売り(今ならパソコンもう1台買える値段で)という昔ではないのだから，なおさらではなかろうか．

鏡の向こうの世界へたどり着くには，仮説的な定説を覆す果てしない旅が必要である，ということを，GPS付きの乗り物で誰でもできるようにするのがCAGE法の今後の課題であるらしいが，当面は，私には手が出ないお高い装置であるのだろう．誰でも買えるくらいの値段になるのは，ずーっと先のことだろうか．そこまで安くはならないということだろうか．ガン抑制遺伝子の発見物語で，Rb遺伝子(網膜芽細胞種の原因遺伝子となる抑制遺伝子)分離をめぐる話は，どうなのだろう．超電導の研究での捏造話も，もともと膜ができるものらしいから，それを応用しようとして，捏造研究ということになったのかもしれないが，紙一重ではなかろうか．科学研究だから，科学の立場で，審査するのは当然の手続きだろうけど，捏造より意味のない捏造騒ぎは，どういう背景なのだろうか．捏造であるかどうかは，科学自体の問題であって，政治や経済などとの関連は，迷路をめぐっていればいいだけの代物である．オバマやプーチン，あるいは，ビルゲーツがフェルマー予想を解いたといって，捏造でないということになっても，信じるものは誰もいない．政治家やお金持ちとして，科学に通じていて理解力があるという評価はあり得るかもしれないが．

 

・ベクトル a, b, cで，a + b = cとすれば，cの逆元-cが存在する． c + (-c) = c -c = 0, a + bを力の平行四辺形とみれば，大きさが同じで向きが逆の力が存在する．

 ・単位の大きさを持つ，OX, OY, OZに平行な単位ベクトルe_1, e_2, e_3をとることができるが，単位ベクトルは，自由ベクトルであるが，固定ベクトルとして扱っても支障がない．

 

[内積と外積]

 

　

[音と絵画と歴史]

歴史と論理の関係を考えるとき，絵画として流れる世界と音として流れる世界が，未分化なまま，音としての意味の現れとして，絵画としての意味の現れとして，戯れる風景の中に，自分がいることを感じることがある．生物の論理は，そのような戯れの中に意味を具象化する歴史のネットワークのような感じを受ける．作曲家や画家が，どういうモチーフで，メロディーや形象を得るのか，絵画の意味があって，メロディーにまとまるのか，メロディーが固まって，形に意味が宿るのか．色はどうなのか．物の配置はどうなのか．私自身の存在は，どう流れていくのか．ベートベンの伝記にある作曲スタイルや，ムンクの叫びなどをみると，芸術の世界には，そういう存在として流れる世界が立ち現れているのじゃないかと，考えたりする．科学の世界も，案外，芸術的な未分化な世界の立ち現れと無縁ではないように感じる．私自身の世界の中の他者として，どのようなシグナルが選択されるのか．数の体系とその妖精たちのコラボのように，音と絵画的な意味の戯れが，自分という存在自身の他者として立ち現れる世界を見ることなら，数学も視覚的なのだろう．見えることなく見，聞こえることなく聞く，存在の歩みや立ち止まりのようなものかもしれない．

 兄弟からは，「あんたは精神年齢が3歳児だ」という評価を受けたが，私の芸術的なセンスが分かりづらいのが原因だろうといっても，まったく承認する気配さえ見せない．あの芸術的な世界の親しみは，身内や肉親でも，他人には伝わりにくいもののようである．

しかし，芸術的世界の親和性が出現する機構は，細胞レベルでは，常時生じているのかもしれない．卵母細胞---卵黄膜(vitelline membrance)---卵胞細胞(→濾胞細胞(follicle cell))とか，胎児---胎盤---卵黄膜内胚葉とか，あるいは脳の仕組みとか，そのような親和性出現機構を示していないだろうか．

高木貞治の『解析概論』にある，4/3 < a < 4/3(4T/3<S<4T/3あるいは0<S-4T/3<0)なら，aは4/3 (Sは4T/3)以外の何物でもない，というような，厳密論証が，実数の連続性を示唆しているという，アルキメデスの求積法も，親和性出現機構の一つかもしれない．

親和性出現機構の数学での例は，「複素多様体の変形理論」などが挙げられるだろうか．出処を異にする指標が，不思議に親和性をもつということは，おそらく出処の違う音の発現と形の発現の親和性に通じているかもしれない．

自然が，時折，歴史の中に届けるものは，他者としての私の存在を共役させる，異質なものどうしの邂逅かもしれない．

虚数に限らず，物理量をベクトルで表すことも，瞬時に誰かがやっていそうに感じるが，実際には，なぜか，時を費やす逡巡があったらしい．それが意味のない足踏みだったのかどうかは，科学のその後が語ることなのだろう．我々の細胞も，語り始めているかもしれない．

音と形，これは，歴史と論理の相互規定を考える，私の一つの観点であるが，岩波現代物理学の基礎『古典物理学I』が，ネタ本である．ネタばらしである．つまり，湯川秀樹の執筆部分である．その私なりのアレンジである．しかし，小平邦彦の複素多様体の変形理論や，音楽や絵画などの芸術，生物特に細胞生物学の話題と結びついたのは収穫である．『不思議の国のアリス』はおとめぽくて，読んでないが，アリスの旅した世界にいけそうなことも収穫である．まあ，乙女が主人公の童話で，私が読んだのは，『一切れのパン』(『パンを踏んだ娘』という題だそうだが，子供の頃読んだときの題はそうだった気がする)だから．

 冗談ついでに，恐竜はなぜ鳥になったのか，カラスに聞いたら，カニ飛び歩きが歩きやすいからだそうである．斜に構えて，飛び歩きすることで，滞空感覚が遺伝子に伝わりやすかったのだそうである．飛べそうな気になったと先祖の記憶が言っていたらしい．そういう説があっても良さそうであるが，聞いたことないが、あるんだろうか．滞空しやすいという感覚が，どうやって鳥に進化したのだろうか．それとも，飛ぶつもりもなかったが、ミクロの世界の都合で、結果、鳥になったのだろうか．

細胞進化は，どういう文字盤になっているのかわからないが、細胞に訊くのが一番なようである．進化とは何か．この問いは，簡単には答えの得られない問題のようである．文字盤が流動化しながら，可触的に関与しているような感じである．ピカソやダリの絵画が細胞に溶け込んで時を刻めば，そんな感覚になるかもしれない．

細胞内に，ピカソやダリの絵画あるいはベートベンやモーツァルトの音楽が，顕微鏡などで確認できるかどうかはわからないが，「細胞は生体の構造的単位であるばかりでなく，代謝・生理・発生・分化・遺伝・進化などすべての生命現象の発現の場であることが実感されるようになった」(『岩波生物学辞典』)のである．

宇宙はがん化ではじまったのか?

原始重力波をキャッチしたかどうかで、精密な観測が必要であるが、可能性が高まったという記事を読んで、なんか宇宙がその始まりで、ガン化したようなメカニズムだなと思ったら、ちょっと興味が生じてきた。がんは、いわば、熱のようなものだから、連想してしまったわけである。ちょっと昔の新書にそういうこと書いてあったから。

最近は、うちわがどうだの、下町のミツプレイの店がどうだのという話題ばかりで(多分、政治家御用達とか、似たようなところは地方都市にはあちこちあるのじゃなかろうか)、まあ、そんなものかなと納得しながら過ごしていたが、さすがに、そんなんだけでは飽きが来る。そこに、自己免疫疾患などに関わる仕組みの一端が解明されたとか、ビッグバン宇宙を観測とかいうニュースがあったから、乗ってみようという気が起こったわけである。やはり、心底興味ある問題でないと、虚しいだけであるから。

 宇宙の始まりというと，ビッグバンということになるが，ぎりぎり，宇宙大爆発の内部の情報につながる，マイクロ波(今度は重力波ということであるが)を観測して，時空構造を含めた，ミクロに凝縮した変転のストームを調べようという目論見だろうか．爆発のエネルギーが，次第に劣化して，熱となって，ビッグバン後の膨張宇宙は，じきに熱死する．宇宙の始まりと終焉のシナリオがビッグバン宇宙論ということらしい．

生命は，逆に，ビッグバンの内側に，ビッグバン後のエントロピーを折りたたんで，組み替えているような感じにも思えるが，案外，そこら，つながってないだろうか．宇宙論と生命が接点を持ち始めてきたということにはならないだろうか．そうかんがえれば，面白いことも，いろいろ出てくるかもしれない．

デカルトの「我おもう。故に我あり」という言葉を考えるたび，私という個の思考は，外界と内界を規定しつつ規定される可伸縮的な脱意味と，意味の付与の格子点のようなものではないかという気がしてくる。

最近は，大きな類空間(量子空間)を考えて，それが，ある意味，0と1の抽象ビット空間を作るようなイメージになっているのだろうか．「我惟う．故に，ビット空間あり」という感じになるのだろうか．いつの間にか，「思う我」が「抽象的に構成されたビット空間」に変わってしまったが，そういう変転が，思うということではなかろうか．「点」という無限の脱意味から，「ひろがり」という意味付与を果たすビット空間にはせる思いというのはあるのだろうか．

ビッグバンが，有限や無限，真空やアトミズム，円環や直線といった概念のアウトソーシング的な意義を担っているのだろうかとか，参考文献を読みすすめれば，いろいろ考えが湧いてくるだろうが，そのうち，まとめてみたいと思う。

 とりあえず，宇宙創世のシナリオに核反応をあてはめるだけではダメだとか，超弦理論の超対称性を満足するために，重力子が出てくるとか，興味をそそる話など，コンパクトに話題が取り上げられているので，コンパクト辞典のようにも使えそうである．難解なアインシュタイン方程式とかを計算できる，数少ない専門家らしいので，本格的な話は，岩波現代物理学叢書『一般相対性理論』などのレベルの本でも読まなければ，わからないのだろうが，当て推量的読解術でやっていこうと思う．

コンピュータのプログラムだったら，機種とかOSの種類とかに関係なく，プログラムする人の目的やデザインを実現してくれて，馴染みやすくて，労力が少なくて済むようなものがいいのだろうが，人間の思いは，人それぞれで，それぞれのこだわりなり癖なりが，どこか残ってくれている方が「思い」らしい感じがして，そういうものも捨て難い．では，その両方を満たしてくれるようなものはないのだろうか．例えば，Java VM(Virtual Machine)というのは，マニュアルによれば，高級言語で書かれたコードを，プログラムが走るハードウェアやOSの違いに依存しない機械語に変換するものらしいが，単に均すだけではない，いわば，「思い」を切り離して，見守るような世界は考えられないだろうか．普段使う言語というものも，日常的に，そういう変換を繰り返しながら，成立しているようにも思える．

 f(x) → yというのも，y=f(x)というのも，y-f(x)=0というのも，「思い」のその時々の，メッセージかもしれない．メッセージを誘発する「思い」の置かれた状況を読み解きながら，「我思う．故に，われ在り」と，非関与的に関与する世界という感じになろうか．「連続」というと，何故か，そんな気がする．

色々な細胞由来の集塊から，どうゆう風に，組織が体系立てられるのか，それがまた，どういう風に，生命現象や病気の仕組みなどの解明につながるのか．そのとき，科学のネットワークが，どう機能していくのか，興味深いことである．これも，カッシーラいうところの，関数的思考の実践例ということになろうか．

同心円を考えれば，同心円に内側から，1,2,3, ---と番号を振ることはできるが，同心円のどの番号を対象に考えるのか決めなければ，1,2,3,---を無限に続けていくか，適当に，対象の番号を決めるしかないが，決められないものは決められないとして，構造をはめ込むようなことをするか，なんらかのことをしないと，夢想に終わる．数体の拡大とかに，幽霊数のような存在を仮定して，その役割を担わせるようなことも考えられだろうか．蛍火の神秘に通じるものがあるのじゃなかろうか．蛍火は，二つの魂の因縁の出会いの光とかならロマンチックだが，宇宙を解明するための関数的なメスであるといえば，哲学的な科学方法論になるだろうか．

 

参考：佐藤文隆著『ビッグバン　こうして宇宙は生まれた』，講談社ブルーバックス

        佐藤文隆著『宇宙論への招待　プリンキピアとビッグバン』，岩波新書

　　 佐藤文隆，小玉英夫著『一般相対性理論』，現代物理学叢書，岩波書店

現代ストリング理論の教科書を読む

---------------------------------------------------------------------------------------------------------------------
``STRING THEORY AND M-THEORY,A Modern Introduction"
K. BECKER, M. BECKER, and J. H. SCHWARZ,
2007
---------------------------------------------------------------------------------------------------------------------

全12章，PDFで700ページほどなので，現時点での翻訳全文と，もし，さらに量が多くなれば，分割して示す．言うまでもないが，誤訳，誤字・脱字など多く含んでいると思うが，参考程度にどうぞ．


「String_Schwarz.pdf」をダウンロード


[目次]
前書き

第1章 序論

第2章 Bosonic string理論

「String_Schwarz2.pdf」をダウンロード

第3章 共形場理論とstring相互作用

「String_Schwarz_3.pdf」をダウンロード

第4章 worls-sheet超対称性を持つストリング

「String_Schwarz_4.pdf」をダウンロード

第5章 時空超対称性を持つストリング

「String_Schwarz5.pdf」をダウンロード
.
.
.

--------------------------------------------------------------------------------------------------------------------

【参考】

岩波物理学基礎講座『古典力学II』から，基礎的な知識を拝借する．といっても，以下は，用語や文脈的な事柄には配慮せず，大雑把なものなので，備忘用のメモ書き代わりのつもりである．


「relativity_abc.pdf」をダウンロード



【感想】

・(x + y)^2=x^2 + 2xy + y^2というような)因数分解の問題で，C=ax +byとかをうまくとらないと，迷路に迷い込むタイプの問題があるが，微分方程式の問題は，そういうタイプ問題が多いということだろうか．ある多項式を因数分解するのに，例えば，C=ax+byというような形にとって代入する場合にすっきりと因数分解できて，それ以外だと，因数分解された形にできないというのは，代入なんて，矛盾ないように機械的にやればどれでも同じになるはずだと思うのだが，因数分解という操作自体が制限のきつい操作なのだろうか，という感じが残る．因数分解という操作に対して，そういう特徴をもった変換の集まりに，共通の特徴を見つけようとかいう問題に発展しそうではないだろうか．

・(群作用)axとxaが非可換である場合という感じ．

・空をみていると，結局，空は青かったなあという感じしか残らないが，何故か，何か別なものをみていたような気になっている．多分，数学だと，かくかくしかじかと定義すれば，矛盾は見つからない．したがって，矛盾するものは，定義を拡張するなりしなければ，分からないものになるが，定義を拡張しようとすると，いろいろ支障が出てくる．しかし，よく見ると，矛盾というより，混合した相の領域がみえてきて，うまくやれば，より統一的な，姿が見えてくるというような感じで，説明できるのかもしれない．普段では気づかない，物事の展開の道理が開けてくる感じだろうか．極小な領域では，仮説的に線形関係を設定してもいいが，そのような粗視化のもとで，どういう意味でその関係が成り立と考えるかは，センスの問題であるとかいう感じになるだろうか．

・絶対真空などはない．「ディラックの海」以来そうであるらしい．絶対空間，絶対時間もアインシュタイン以来ないらしい．絶対真空にして，相対的な世界を作り出す真空を無縁に存在せしめるなんてことは考えられないのだろうか．「色即是空，空即是色」というが，知はその「間」に漂う無縁者という感じになるのだろうか．つまり，キリスト教的にいえば，「なぜ」と問う存在者(あるものである)なのかということだろうか．キリストが父神に「なぜ」と問い返す場面とかから．

・「時空概念の変革」ということが，現代の物理理論では，特に，アインシュタインの相対性理論以来，重要なテーマの一つになっている．ストリング理論では，ミクロ時空が増殖したり，あるいは，消滅したりという様子を，基本的な対象の，物質性と時空性の，不可分離な構成という感じでとらえているのだろうか．その場合，質量という概念が，その鍵となる概念になっているということだろうか．質量は，「アインシュタインの関係式」からも分かるように，変わりうるわけだから．そういう感じが，ある意味では，生命を司る，遺伝子に潜む謎に通じている気がする．こういう感じを，あるいは，ポストモダン的というのかもしれない．二価化するということは，情報性の獲得であるとも言えるわけだから，情報という非物質性を物質化して，時空自由度に代わる自由度を機能化していく，という感じもあるだろうか．


・ポスト・モダン的ということを，情報化と言い換えてもいい感じである．量子化学だとか，遺伝子学だとか，現代科学の形式が，情報化という手法をカギにしている感じであるという意味で．

物理の「スピン」という概念を，ヒッグスの機構のようなことを通して，一般的な量子化の，仮想プロセスとして通していく感じなのだろうか．そういう手法が一般的であるとすれば，研究を進めるには，そこでのコミュニケーションの緊密性が，より以上に，必要とされるようになるのかもしれない．カルチャーの壁というより，縦横につながるカルチャーの網の目を，主題の中に具体化して，実現していくようなコミュニケーションのあり方が，より必要な状況が，科学あるいは学問研究にはあるのだろう．それは，高度に専門的な事柄に属すると同時に，俗にいう素人状況にも影響する一般性もあるのではなかろうか．

極限的仮想超対称性の破れの機構と，遺伝子コードの解読に共通する面があるとすれば(あくまで仮に)，遺伝子の難しさは，自然が選択する理論的な機構と密接な関係にあるということなのかもしれない．そういう意味で，分野の異なる研究の間にも，自ずと緊密なコミュニケーションの要求が組み込まれているという状況に，現代科学はなっているのかもしれない．私などは，一人で本読んで，ひねくり回して，好き勝手ブログしていれば満足なのだが，科学研究の現場はそうもいかないのだろう．どうやって，相互に検証し合うのかとか，どうやって，それを科学的成果として確認して，共有していくのかとか，具体化しなければならないだろうから．

・対称性と質量値の縮退---SU(6)対称性に関する説明のところ(『素粒子論』)にあったが，時間τと関連づけて考えるのもありそうな気がする．縮退は，量子力学的な観測の確率性に関連することのようだが，ある固有値に属する固有ベクトルの張る閉部分空間(固有空間)の次元dが1でない場合を言うらしいので，時間τとどう関連するのかも，結構複雑そうである．

・整数論 ---「不可分な連鎖」--- 自己双対 --- ４次元ソリトン(インスタントン)?　

・gravity(vielbein formalism)，４脚ベクトル形式の重力 --- 場の自由度が，物質や場の粒子に制約的に転換される(ソリトン的な波の伝播になる)．自由度の相互制約的変転ソリトン波的な感じ?