宇宙の法を握る「カラビ＝ヤウ多様体」

　Ｔ双体性とミラー対称性がどのような形で密接に関係しているのか、それを理解する単純な方法がある。
多様体Ｍを、半径ｒの二つの円の積であるトーラスとする。
その鏡像Ｍ'もトーラスで、それは半径１／ｒの二つの円の積だ。
さらに、ｒはきわめて小さいとする。
Ｍはとても小さいので、それに伴う物理を理解しようとしたら、量子効果を考慮しなければならない。
しかし、ｒがきわめて小さければ１／ｒはとても大きく、量子効果は十分に無視できるため、ミラー多様体Ｍ'から物理を導くのは簡単になる
このようにミラー対称性は、Ｔ双体性という姿を装って、計算をとてつもなく単純にしてくれる。

　すべての部分多様体（円）の半径を反転させると、それらすべての円からつくられる大きな多様体は、半径こそ最初とは違うものの、やはりトーラスである。
そのため、多様体とその鏡像がトポロジー的に等価なので、この例は自明であると呼ばれる。
Ｋ３曲面からなる四次元の例も、すべてのＫ３曲面がトポロジー的に等価であるため、同じ意味で自明だ。
しかし、カラビ＝ヤウ・スリーフオールドが関係する六次元の例は、もっと興味深い。
その多様体の構成部品には、三次元トーラスが含まれる。
Ｔ双体性を適用すると、それらのトーラスの半径が反転する。
非特異なトーラスでは、半径が変わってもトポロジーは変わらない。
しかし、もとの部分多様体がすべて「よい」［非特異な］種類だったとしても、各部分が非自明な形で組み合わさっていることがあるため、半径を変えることで大きな多様体のトポロジーが変化することがある。

　比喩を使えばもっともよく理解できるかもしれない。
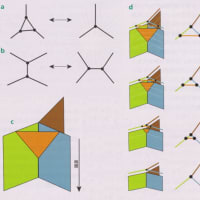
線分（棒）の束があれば、それを粘土板に円形に刺していって、円筒をつくることができる。
または、同じ線分を使って、円筒（表裏がある）をつくる代わりに、ひねりを入れて組み合わせることで、片面しかないメビウスの帯をつくることもできる（下図参照）。
つまり、同じ部品、同じ部分多様体を使っても、まったく異なるトポロジーをもつ物体がつくられるのだ。


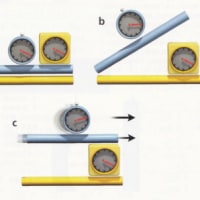
図：地面と平行に（表面に沿わせて）棒をもったまま赤道を1周すると，円筒が描かれる。
一方，地球を1周するあいだに棒を徐々に180度回転させると，メビウスの帯と呼ばれる複雑な曲面が描かれる。

　Ｔ双体性による変化を施し、部分多様体を組み合わせる方法を変えると、トポロジー的には異なるものの物理の観点からは区別がつかない二つの多様体が得られるということだ。
それがミラー対称性の意味するところの一部だが、それですべてではない。
この双対性のもつもう一つの興味深い特徴として、ミラーペアは互いに符号が反対のオイラー数（標数）をもっていなければならない。
ここで取り上げている部分多様体のオイラー標数はすべてゼロであり、半径を反転させても変化しない。

　いま述べたことは、「よい」（非特異な）部分多様体に関しては正しいが、「悪い」（特異な）部分多様体については成り立たない。
Ｔ双体性は、それらの悪い部分多様体のオイラー標数を、＋１から－１へ、－1から＋１へ交換する。
それらの悪い多様体は、モジュライ空間Ｂ上の悪い点に対応する。
「ミラー対称性における興味深い事柄、すなわちトポロジーの変化はすべて、Ｂの頂点で起こる」
このように、新たに浮かび上がってきた描像では、この空間Ｂがミラー対称性の中核を占める。

　以前は、この現象全体が謎に包まれていた。
「ＸとＸ'という二つの多様体があって、それらは何か関連しているけれど、共通してもっているのが何なのかはなかなかわからなかった」。
その共通してもっていたのが、このもう一つの物体Ｂだったのだが、はじめは誰もそれについて知らなかったのだ。

グロスは、Ｂを一種の青写真だと考えた。
その青写真をある視点から見ると、ある構造物（多様体）が組み上がり、別の視点から見ると別の構造物が組み上がる。
そしてそれらの違いは、Ｂ上の、Ｔ双体性がうまくはたらかない奇妙な（特異な）点から生じ、その結果としていろいろな事柄が変化するのだ。

　以上が、ＳＹＧのレンズを通して見たミラー対称性に対する、現在での描像だ。
このＳＹＧの大きな利点の一つは、ミラー対称性の謎が少し解けたことだ。
数学者がそれを気に入ったのは、ミラー対称性の由来に関する幾何学的描像を示してくれたからで、ひも理論に頼らなくてもその描像は使うことができる。
ミラーペアを構築するプロセスも提供してくれる
ＳＹＧはいまだ予想であって、いくつか限られたケースでしか証明されておらず、一般的な形では証明されていないことは、覚えておかなければならない。

　ホモロジー的ミラー対称性は、一九九三年にコンツェヴィッチによってはじめて明らかとなり、それ以来発展を続け、物理学と数学の両方においてかなりの研究を促している。コンツェヴィッチのアイデアはＤ－ブレーンの発見より一年か二年早かったが、ホモロジー的ミラー対称性を記述する方法としては、おそらくＤ－ブレーンを使う方法がもっとも単純だろう。

物理学者はＤ－ブレーンを、開いたひもの端がくっつく部分曲面として考える。
ホモロジー的ミラー対称性はＤ－ブレーンより前に導かれたが、第二次ひも革命後にひも理論、すなわちＭ理論のもっとも基本的な構成要素の一つとなったＤ－ブレーンを、もっと洗練された形で記述する。
ホモロジー的ミラー対称性の根底にある重要な考え方の一つが、その現象に関わるＤ－ブレーンにはＡ－ブレーンとＢ－ブレーンの二種類があるというものだ。
カラビ＝ヤウ多様体のミラーペアＸとＸ'があれば、Ｘ上のＡ－ブレーンはＸ'上のＢ－ブレーンと等しい。
この簡潔な定式化によって、数学者は、ミラー対称性が何であるかを明確に表現できるようになった。
そしてその表現から、他のすべての事柄を導くことができる。

　それはちょうど、形の異なる二種類の建築用ブロックがあるようなもので、それでも、それらを積み上げると、まったく同じ種類の構造をつくることができる。
ホモロジー的ミラー対称性が仮定するＡ－ブレーンとＢ－ブレーンの対応関係も、それと似ている。

　Ａ－ブレーンは、「シンプレクティツク幾何」と呼ばれるもので定義される物体で、一方のＢ－ブレーンは「代数幾何」の物体だ。
シンプレクティツク幾何は、カラビ＝ヤウ多様体の中核をなすケーラー幾何の概念を含んでいるが、それよりもっと一般的だ。
微分幾何における空間はふつう、対角線に対して対称的な計量で記述されるが、シンプレクティツク幾何における計量は対角線に対して反対称で、対角線をまたぐと符号が変化する。

　それら二つの幾何学分野はまったく別物だと考えられていたので、とある人物が現れて、ある空間の代数幾何が別の空間のシンプレクティツク幾何と等価だと言うと、大きな衝撃が走った。
かけ離れた二つの分野をつなぎ、ミラー対称性によってそれらがある意味関連していることを発見するというのは、一つの分野の手法をもう一つの分野に使えるようになるため、数学においてなしえる最高の成果の一つだ。
ふつうはそれによって水門が開かれ、何個かのフィールズメダルが生まれる。　
そんな中、ホモロジー的ミラー対称性は他の数学分野に広がり、ＳＹＧにも手を伸ばしている。
しかし現段階では、二つのあいだの厳密な数学的等価性はない。
それでも互いに支え合っている。
もしどちらも正しければ、いずれは、何らかのレベルで二つは等価であることが明らかになるはずだ。

　私たちは、ＳＹＧやホモロジー的ミラー対称性などの研究によって、ミラー対称性の意味を解き明かそうとしている。
しかし、その探究がどこまで進むか、どこへ行き着くかは、誰にもわからないが、その出発点はわかっている。
それは、カラビ＝ヤウという名をもつコンパクトなケーラー多様体の異常な性質の発見だ。