ミラー多様体には、それまで関係ないと思われていた物体を並べることで見えてくる魅力的な特性がいくつかある。
カラビ=ヤウ多様体にはさまざまな次元(奇数次元および偶数次元)の穴が空いているが、グリーンとプレッサーは、ペアのあいだにある興味深いパターンを見つけた。
すなわち、一つの多様体に空いている偶数次元の穴の数が、そのミラーに空いている奇数次元の穴の数と等しく、その逆も成り立つのだ。
つまり、偶数と奇数が入れ替わるということは、形状や基本的な幾何構造がまったく異なるのに、それぞれの穴の総数は同じであるということだ。
それはトポロジーを通して見てみると理解しやすいかもしれない。
たとえば、カラビ=ヤウのミラーペアどうしのオィラー標数は符号が互いに反対なので、おおざっぱに言ってもまったく異なるトポロジーをもつ。
オイラー標数の値自体は空間に関する情報の一部しかもっておらず、立方体、正四面体、球などまったく違って見える数多くの空間がすべて同じオイラー標数をもちうる。
しかし、オイラー標数を分解し、空間の内部構造に関するもっと詳しい情報を含んでいる、ベッチ数と呼ばれる整数の和や差で表せば、そのおおざっぱさを改善できる。
図1:曲面(ここでも向き付け可能なすなわち表裏のある曲面)どうしはベッチ数を比較することによってトポロソー的に区別できる。一般的にベッチ数からは2次元曲面にそれを2つの部分に切り離すことなしに1周切り込みを入れる方法が何通りあるかがわかる。球面をそのように切る方法は存在しないので球面のベッチ数は0となる。一方ドーナツでは2つに分けずに切る方法が図のように2通りあるのでベッチ数は2となる。
しかし、互いに異なる多様体のトポロジーをもっと詳しく記述することもできる。
それぞれのベッチ数はさらに、ホッジ数と呼ばれるもっときめ細かい数の和となっている。
ホッジ数を使うと、空間の部分構造をさらに高解像度で捉えることができる。
その情報 は、いわゆるホッジダイヤモンドの中に詰め込まれている。
図2:(複素3次元)カラビ=ヤウ多様体の詳細なトポロジー的情報は,ホッジダイヤモンドと呼ばれる×4の数の表に含まれている。ホッジダイヤモンドだけではカラビ=ヤウ多様体をただ1つに特定できない場合あるが,異なるホッジダイヤモンドをもつ多様体は必ずトポロジー的に異なる。表に示した2つのホッジダイヤモンドは互いに鏡像になっており,カラビ=ヤウ多様体とそのミラーパートナーに対応している。
ホッジダイヤモンドを使うと、ミラー対称性の「ミラー」を視覚的に表すことができる。
格子状に並んだ16個の数は、ある6次元カラビ=ヤウ多様体に対応する。
そして、コンピュータで生成した多数のカラビ=ヤウ多様体を調べた結果、著しいパターンが発見された。
それらの多様体はペアをつくっていて、一方の偶数次元の穴の数がもう一方の奇数次元の穴の数と等しくなっているように見えた。
この観測された、二つの多様体における穴の数、形状と大きさの設定、およびホッジ数の交換関係は、単なる数学的な偶然かもしれない。
しかし、何が決定的だったかと言えば、互いに異なるカラビ=ヤウのペアが同じ物理を生じることを証明したことだ。
それがミラー対称性の真の定義であり、それは単なる二つの数の交換関係をはるかに凌ぐ。
物理学者は、与えられた多様体を場の量子論と関連づける方法をもっている。
しかし、多様体はふつう無限個のサイクルをもっているため、近似としてその個数を、扱うことのできる有限の値まで引き下げる。
そのプロセス、つまり、可能な設定が無限個あるものを取り上げ、いくつかの値しか許されないとしてしまうことを、「量子化」という。
その際には、もともとの方程式-サイクル、ひいてはコホモロジーに関する方程式Iに量子補正をおこなう。
そのためそれを、「量子コホモロジー」と言われる。
実は、そのような量子補正をおこなう方法は一通りだけではない。
ミラー対称性のおかげで、カラビ=ヤウ多様体を一つ取り上げると、それと物理的に等価なミラーパートナーをつくることができる。
そのパートナーは、同じ場の量子論を表現する、一見して異なるが本質的に等価な二種類のひも理論、タイプⅡAとタイプⅡBによって記述される。
量子補正の計算はBモデルの方が比較的簡単で、そのとき量子補正は実はゼロになる。
Aモデルでの計算は量子補正がゼロでないため、現実的に不可能だ。
最新の画像[もっと見る]
-
 タイムトラベルとタイムマシン?
10年前
タイムトラベルとタイムマシン?
10年前
-
 パウリの夢の数式に「虚数」が生み出された!
10年前
パウリの夢の数式に「虚数」が生み出された!
10年前
-
 「微細構造定数」137とパウリ&ユング
10年前
「微細構造定数」137とパウリ&ユング
10年前
-
 宇宙インフレーション 超弦理論
10年前
宇宙インフレーション 超弦理論
10年前
-
 拡張標準モデルとは?
11年前
拡張標準モデルとは?
11年前
-
 拡張標準モデルとは?
11年前
拡張標準モデルとは?
11年前
-
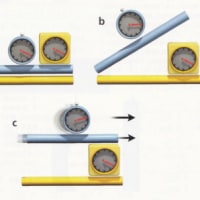 相対性理論とローレンツ対称性
11年前
相対性理論とローレンツ対称性
11年前
-
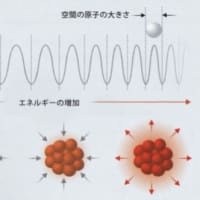
 宇宙の起源に新説か?
11年前
宇宙の起源に新説か?
11年前
-
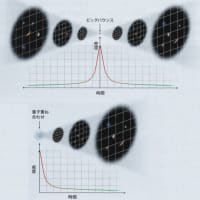
 宇宙の始まりは「ビッグバウンス」?
11年前
宇宙の始まりは「ビッグバウンス」?
11年前
-
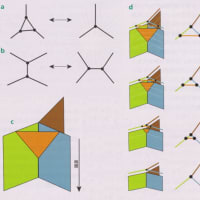 「スピンの泡」が時空に対応する、ループ量子重力
11年前
「スピンの泡」が時空に対応する、ループ量子重力
11年前










※コメント投稿者のブログIDはブログ作成者のみに通知されます