前回は点A・Bからそれぞれ実軸平面上に写し出していたホログラムの説明をしました。二つの球体上の点Pと点Qが点Oに近づくと、ホログラムとして映し出された物体は非常に小さくなっています。同様に点Aと点Bに近づくと無限遠の地平面を見ていることになります。
このことは、我々が認識している空間を地球上の3次元空間に例えると、無限の距離としての地平線から、極小の素粒子までを観察していることになります。したがって、超微細なプランク定数(ħ)という特異点まで到達するはずです。
今回は下の図を見てください。前回の時とは正反対となる事象を、前回の図に書き加えています。すなはち、点Oから観察した時の3次元空間を考察することになります。
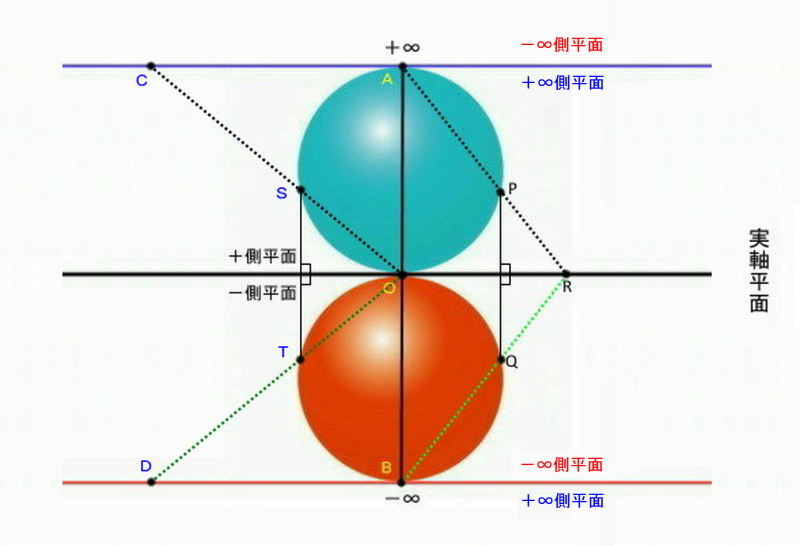
図:3次元空間のプランク定数とビッグバン
上の図は、実軸平面上の点Oから+∞側平面と-∞側平面に描かれるホログラムを示しています。この図も上部の青色球体について考察すれば良いのかも知れませんが、「リザムの実宇宙図」との関係で上下の球体を使っています。
前回載せていました左側の図(マカバ)から推察できますように、実軸空間は完全に孤立した空間構造になっています。だから、上の図の+∞側平面より上方の空間は-∞側平面内の空間に接続されています。同様に-∞側平面より下方の空間は+∞側平面内の空間として接続されています。ちょうど鏡の表と裏が反転している状態に相当します。
さて、この図の球体の点Oから出発した二つの点Sと点Tは、それぞれ+∞の点Aと―∞の点Bに進んでいくことになります。この時、とりあえず点Aに進んだ点Sは、+∞側平面上の点S上に射影された空間を見ることになります。そして、点Sが点Aに非常に接近した時には、特異点Aを見ることになります。
この状態は、我々が宇宙を眺めている時の状態(ホログラム)を示していて、最初は太陽系内の惑星や銀河系内の星々が観測されます。そして、もっと遠距離に存在する銀河や銀河団そして超銀河団なども見えてきます。
最終的には、特異点Aに達する頃には現代宇宙理論でいわれている所のビッグバン理論という宇宙創造の場所に行き着くことになります。そして、今度はビッグバン以前の宇宙が存在したかどうかという疑問に行き着くのです。
しかし、このことは+∞側平面上での観測であり、現代の物理学では-∞側平面についての考察がなされていません。
上で書きましたように、+∞側平面と-∞側平面が背中合わせの状態になっているとするならば、この図の+∞のA点と-∞のB点は「ワームホール」あるいは「ブレーン」として繋がっていても良いはずです。
前回に出てきました実軸平面と今回の「ブレーン」は全く同じ関係で在ると考えられます。そして、どちらも我々人類にはホログラムとして認識されているのです。
ホログラムであるならば、「光」しか捉えていませんので、そこに写された物質には質量が存在しないと言えるはずです。また、+側平面と-側平面のホログラムと実軸平面上の物体との関係も「ブレーン」上の現象と言えるでしょう。
今回は、ここで終了しますが、「ブレーン」という単語が出現していますが、この単語については、「幅を持った膜のようなもの」として捉えていてください。
今回は下の図を見てください。前回の時とは正反対となる事象を、前回の図に書き加えています。すなはち、点Oから観察した時の3次元空間を考察することになります。

図:3次元空間のプランク定数とビッグバン
上の図は、実軸平面上の点Oから+∞側平面と-∞側平面に描かれるホログラムを示しています。この図も上部の青色球体について考察すれば良いのかも知れませんが、「リザムの実宇宙図」との関係で上下の球体を使っています。
前回載せていました左側の図(マカバ)から推察できますように、実軸空間は完全に孤立した空間構造になっています。だから、上の図の+∞側平面より上方の空間は-∞側平面内の空間に接続されています。同様に-∞側平面より下方の空間は+∞側平面内の空間として接続されています。ちょうど鏡の表と裏が反転している状態に相当します。
さて、この図の球体の点Oから出発した二つの点Sと点Tは、それぞれ+∞の点Aと―∞の点Bに進んでいくことになります。この時、とりあえず点Aに進んだ点Sは、+∞側平面上の点S上に射影された空間を見ることになります。そして、点Sが点Aに非常に接近した時には、特異点Aを見ることになります。
この状態は、我々が宇宙を眺めている時の状態(ホログラム)を示していて、最初は太陽系内の惑星や銀河系内の星々が観測されます。そして、もっと遠距離に存在する銀河や銀河団そして超銀河団なども見えてきます。
最終的には、特異点Aに達する頃には現代宇宙理論でいわれている所のビッグバン理論という宇宙創造の場所に行き着くことになります。そして、今度はビッグバン以前の宇宙が存在したかどうかという疑問に行き着くのです。
しかし、このことは+∞側平面上での観測であり、現代の物理学では-∞側平面についての考察がなされていません。
上で書きましたように、+∞側平面と-∞側平面が背中合わせの状態になっているとするならば、この図の+∞のA点と-∞のB点は「ワームホール」あるいは「ブレーン」として繋がっていても良いはずです。
前回に出てきました実軸平面と今回の「ブレーン」は全く同じ関係で在ると考えられます。そして、どちらも我々人類にはホログラムとして認識されているのです。
ホログラムであるならば、「光」しか捉えていませんので、そこに写された物質には質量が存在しないと言えるはずです。また、+側平面と-側平面のホログラムと実軸平面上の物体との関係も「ブレーン」上の現象と言えるでしょう。
今回は、ここで終了しますが、「ブレーン」という単語が出現していますが、この単語については、「幅を持った膜のようなもの」として捉えていてください。












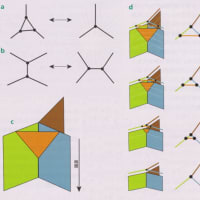
私はもっと簡単なことを考えました。互いに等角で交わる直線の交角がユークリッドn次元空間でどうなるか?そこでこの角を計算する式を求めました。この式で計算すると1次元空間ではπ(この角度を表すには2次元空間が必要)2次元空間では3分の2πです。3次元空間で計算してみるとメタンの分子模型を表す角度になりました。
空間の次元が大きくなるとこの角度は小さくなっていきます。次元が無限に大きくなると角度は2分のπに収縮していきます。実際にこのような空間があるのでしょうか?単に数学上のものでしょうか?
量子力学にはヒルベルト空間という無限次元ベクトル空間と言うものがありますが。