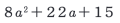数学検定 過去問題 2級（高校2年程度） 問題3. 分母の有理化
https://www.su-gaku.net/suken/support/past_questions/
〔2級〕１次：計算技能検定
問題3. 次の式の分母を有理化しなさい。
以下のようにすれば簡単に答えが出る。
expr = 2 / (sqrt(Sym(7))-1)
factor(simplify(expr)) |> string
"(1 + sqrt(7))/3"
以下はお勧めできない。
using SymPy
@syms a b c
expr = a / (sqrt(b) - c)
denominator0 = sqrt(b) + c
numerator = a * denominator0
denominator = expand((sqrt(b) - c) * denominator0)
expr = numerator / denominator
together(expr(a => 2, b => 7, c => 1)) |> string # (1 + sqrt(7)) / 3
数学検定 過去問題 2級（高校2年程度） 問題2. 因数分解
https://www.su-gaku.net/suken/support/past_questions/
〔2級〕１次：計算技能検定
問題2. 次の式を因数分解しなさい。
using SymPy
@syms a
factor(8a^2 + 22a + 15) |> string # (2*a + 3)*(4*a + 5)
数学検定 過去問題 2級（高校2年程度） 問題1. 式の展開
https://www.su-gaku.net/suken/support/past_questions/
〔2級〕１次：計算技能検定
問題1. 次の式を展開して計算しなさい。
using SymPy
@syms x
expand((x + 1)^2 * (x - 1)^2) |> string # x^4 - 2*x^2 + 1
数学検定 過去問題 準1級（高校3年程度） 問題7. 極限
https://www.su-gaku.net/suken/support/past_questions/
〔準１級〕１次：計算技能検定
問題7. 式 (x^2 + 2x - 3) / (x^(1/3) - 1) において，x → 1 のときの極限値を求めなさい。
using SymPy
@syms x
expr = (x^2 + 2x - 3) / (x^(1/3) - 1)
limit(expr, x, 1) # 12.0
蛇足
x = 1 では，
(x^2 + 2x - 3)(x => 1) # 0
(x^(1/3) - 1)(x => 1) # 0
となるが，
one = big"1"-big"1e-30"
0.9999999999999999999999999999989999999999999999999999999999999999999999999999969numerator = (x^2 + 2x - 3)(x => one)
4.000000000000000000000000000001000000000000000017394736293538355827705813116e-30
denominator = (x^(1/3) - 1)(x => one)
3.333333333333333148296162562472798818283610873852475485997784176552630956246e-31
誤差を考慮して，numerator は 4e-30, denoinator は 10e-31 / 3 である。
よって，与式の x → 1 の極限は
numerator / denominator = 4e-30 / (10e-31 / 3) = 12.0 である。
数学検定 過去問題 準1級（高校3年程度） 問題6. 双曲線の焦点
https://www.su-gaku.net/suken/support/past_questions/
〔準１級〕１次：計算技能検定
問題6. xy 平面上の双曲線 x^2/36 - y^2/64 = -1 の焦点の座標を求めなさい。
この双曲線の焦点は y 軸上にある。
焦点は (0, sqrt(64 + 36)) と (0, -sqrt(64 + 36))
すなわち，(0, 10) と (0, -10)
数学検定 過去問題 準1級（高校3年程度） 問題5. 不定積分，定積分
https://www.su-gaku.net/suken/support/past_questions/
〔準１級〕１次：計算技能検定
問題5. 次の問いに答えなさい。ただし，ℯ は自然数の底を表します。
(1) 不定積分を求めなさい。∫(x^2/2 + 3x) * ℯ^(x/2) dx
(2) 定積分を求めなさい。∫(x^2/2 + 3x) * ℯ^(x/2) dx, x の範囲 0 〜 2
(1)
@syms x
expr = (x^2/2 + 3x) * ℯ^(x/2)
integrate(expr) |> string # (x^2 + 2*x - 4)*exp(x/2) 数学の解答としては "+C" とか書くか
(2)
integrate(expr, (x, 0, 2)) |> string # 4 + 4*E E は ℯ のこと
数学検定 過去問題 準1級（高校3年程度） 問題4. 複素数
https://www.su-gaku.net/suken/support/past_questions/
〔準１級〕１次：計算技能検定
問題4. 複素数 z = -２ - i について，次の問いに答えなさい。ただし，i は虚数単位を表します。
(1) z の絶対値を求めなさい。
(2) z の偏角をθとします。このとき，sin４θ の値を求めなさい。
(1)
SymPy を使わないバージョン
z = -2 - 1im # -2 - 1im
abs(z) # 2.23606797749979
sqrt(real(z)^2 + imag(z)^2) # 2.23606797749979
real(z)^2 + imag(z)^2 # 5
よって √5
SymPy を使って
@syms a::real b::real c::complex z::complex
z = complex(a, b) # a + ib
expr = abs(z) # √(a^2 + b^2)
expr(a => -2, b => -1) # √5
(2)
c = z^4
expand(c) |> string # a^4 + 4*I*a^3*b - 6*a^2*b^2 - 4*I*a*b^3 + b^4
実部は
(a^4 -6a^2*b^2 +b^4)(a => -2, b => -1) # -7
虚部は
4(a^3*b - a*b^3)(a => -2, b => -1) # 24
つまり -7 + 24im
以下のようにしてもよい。
c(a => -2, b => -1).evalf() |> string # "-7.0 + 24.0*I"
偏角 θ は tan(θ) = 24/(-7)
θ = atan(24/7) # 1.2870022175865687
sin(θ) # 0.96
分数の形で求めるなら，
絶対値は
abs(c)(a => -2, b => -1).evalf() # 25.0
sin(θ) は定義より，（下図を参照して） 24/25
検算
sin(atan(24/7)) - 24/25 # 0.0
using Plots
plot([0, -7, -7, 0], [0, 24, 0, 0], aspect_ratio=1)
数学検定 過去問題 準1級（高校3年程度） 問題3. 内積
https://www.su-gaku.net/suken/support/past_questions/
〔準１級〕１次：計算技能検定
問題3. 3 つの単位ベクトル a, b, c が 2a + 3b + 4c = 0 を満たすとき，a と c の内積 a・c を求めなさい。ただし，0 は零ベクトルを表します。
c を移行して，両辺を2乗する。
# (2a + 4c)^2 = (3b)^2
# 4|a|^2 + 16a・c +16|c|^2 = 9|b|^2
# 4 + 16a・c + 16 = 9
# a・c = -11/16
数学検定 過去問題 準1級（高校3年程度） 問題2. 平行な 2 直線間の距離
https://www.su-gaku.net/suken/support/past_questions/
〔準１級〕１次：計算技能検定
問題2. xy 平面上の 2 直線 3x + 4y - 20 = 0 と 3x + 4y + 50 = 0 の間の距離を求めなさい。
愚直な方法。2直線は平行。この 2 直線と垂直に交わる直線との交点をもとめ，ユークリッド距離を計算する。
using SymPy
@syms x
eq1 = (-3x + 20) / 4
eq2 = (-3x - 50) / 4
eq3 = 4/3 * x
plot(eq1, xlims=(-20, 20), size=(300, 300), aspect_ratio=1, label="eq1")
plot!(eq2, label="eq2")
plot!(eq3, label="eq3")
x1 = solve(Eq(eq1, eq3))[1]
y1 = eq3.subs(x, x1)[1]
x2 = solve(Eq(eq2, eq3))[1]
y2 = eq3.subs(x, x2)[1]
scatter!([x1, x2], [y1, y2])
sqrt((x1-x2)^2 + (y1-y2)^2) # 14
別法
点 (X, Y) と直線 ax + by + c = 0 の距離は，abs(aX + bY + c) / sqrt(a^2 + b^2) である。
3x + 4y - 20 = 0 上の任意の点，たとえば (0, 5) から，3x + 4y + 50 = 0 への距離は，
abs(3*0 + 4*5 +50) / sqrt(3^2 + 4^2) # 14.0
暗算でもできるが，14 が答えである。
数学検定 過去問題 準1級（高校3年程度） 問題1. 不等式を解く
https://www.su-gaku.net/suken/support/past_questions/
〔準１級〕１次：計算技能検定
問題1. 次の不等式を解きなさい。
using SymPy
@syms x
eq1 = log(1/2, 2x)
eq2 = log(1/2, x^2-2x+3)
solve(Eq(eq1, eq2)) # [1, 3]
以下はエラーになる。
solve(Ge(eq1, eq2))
図を描いて確定する。
using Plots
plot(eq1, xlims=(0.0, 3.5), ylims=(-3, 5), size=(300, 300), label="eq1")
plot!(eq2, label="eq2")
0 < x < 1, 3 < x
数学検定 過去問題
https://www.su-gaku.net/suken/support/past_questions/
1級（大学程度・一般）
〔１級〕１次：計算技能検定
問題7. xyz空間における領域 V={ (x，y，z) | ０≦x≦y≦z≦１} に対して，次の３重積分を求
めなさい。
紙と鉛筆でやるとなると，めんどくさいんだろうなあ。
using SymPy
@syms x y z
integrate(x^3 * y^2 * z, (x, 0, y), (y, 0, z), (z, 0, 1)) # 1/252
数学検定 過去問題
https://www.su-gaku.net/suken/support/past_questions/
1級（大学程度・一般）
〔１級〕１次：計算技能検定
問題6. 次の行列の固有値を求めなさい。
[ 3 -1 2
-2 5 -3
1 -3 2 ]
定石通り，以下の固有方程式を解く。
using SymPy
@syms λ
M = [ 3-λ -1 2
-2 5-λ -3
1 -3 2-λ]
ev = det(M) # -λ^3 + 10*λ^2 - 18*λ + 4
solve(ev) # 2, 4 - sqrt(14), sqrt(14) + 4
別解というか，こちらの方がよい
M = [ 3 -1 2
-2 5 -3
1 -3 2 ]
#=
3×3 Matrix{Int64}:
3 -1 2
-2 5 -3
1 -3 2
=#
sympy.Matrix(M).eigenvals()
#=
Dict{Any, Any} with 3 entries:
4 - sqrt(14) => 1
sqrt(14) + 4 => 1
2 => 1
=#
数学検定 過去問題
https://www.su-gaku.net/suken/support/past_questions/
1級（大学程度・一般）
〔１級〕１次：計算技能検定
問題5. 0 以上の整数値をとる確率変数 X が下の確率分布に従うとき，次の問いに答えなさい。
ただし binomial(n, r) は二項係数を表します。
P(X=k) = binomial(k+2, k) * (1/10)^2 * (9/10)^k * (1/10)
(1) X の期待値 E(X) を求めなさい。
(2) X の分散 V(X) を求めなさい。
これは，数値解なので Julia プログラムを書いても求まる（ただし，途中までの部分和）
e = 0
for k = 0:4000
p = binomial(k+2, k) * (1/10)^2 * (9/10)^ k * (1/10)
e += k*p
end
println(e) # 27.000000000000046 期待値
v = 0
for k = 0:4000
p = binomial(k+2, k) * (1/10)^2 * (9/10)^ k * (1/10)
v += (k-s)^2*p
end
println(v) # 270.00000000000006 分散
SymPy では summation() を使う。
using SymPy
@syms k
p = binomial(k+2, k) * (1/10)^2 * (9/10)^ k * (1/10)
mean = summation(k * p, (k, 0, oo)) # 27.0
variance = summation((k-mean)^2 * p, (k, 0, oo)) # 270.0
数学検定 過去問題
https://www.su-gaku.net/suken/support/past_questions/
1級（大学程度・一般）
〔１級〕１次：計算技能検定
問題4. 関数f(x)＝x^2 * e^(－x) について，次の問いに答えなさい。ただし，eは自然対数の底を表しま
す。
① f(x) の第5次導関数の x=-1 における値f^{(5)}(-1) を求めなさい。
② f(x) の第10次導関数の x=-1 における値f^{(10)}(-1) を求めなさい。
using SymPy
@syms x
f = x^2 * ℯ^(-x) # x^2*exp(-x)
diff(f, x, 5).subs(x, -1) # -31*E ie. -31ℯ
diff(f, x, 10).subs(x, -1) # 111*E ie. 111ℯ
ちなみに，
diff(f, x, 5) |> string # "(-x^2 + 10*x - 20)*exp(-x)"
diff(f, x, 10) |> string # "(x^2 - 20*x + 90)*exp(-x)"
数学検定 過去問題
https://www.su-gaku.net/suken/support/past_questions/
1級（大学程度・一般）
〔１級〕１次：計算技能検定
問題3. xyz 空間における 2 平面 3x−y−2z＝6, x + 2y - 3z = 4 が交わってできる直線を l とします。l を含み，点(1, -1, -2) を通る平面の方程式を求めなさい。
using SymPy
@syms x, y, z, k
2 平面の方程式を a, b とおく。
a = 3x - y - 2z - 6 # = 0
b = x + 2y - 3z - 4 # = 0
求める平面の方程式は a + k * b = 0 とおける。
eq1 = a + k * b
# k*(x + 2*y - 3*z - 4) + 3*x - y - 2*z - 6
この平面が (x, y, z) = (1, -1, -2) を通るので，x, y, z に代入し，eq1 = 0 を k について解く。
solve(eq1.subs([(x, 1), (y, -1), (z, -2)]), k)
k = -2 である。
eq1 に k = -2 を代入して解を得る。
eq1.subs(k, -2)
# x - 5*y + 4*z + 2
