算額（その1093）

算額（その1093）

五十二 岩手県一関市 舞草観音堂 正慶山聖観世音堂 天保14年(1843)
山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市. http://www.wasan.jp/yamamura/yamamura.html
キーワード：円4個，正三角形，正方形

正方形の中に正三角形，大円 3 個，小円 1 個を容れる。小円の直径が与えられたとき，大円の直径を求めよ。

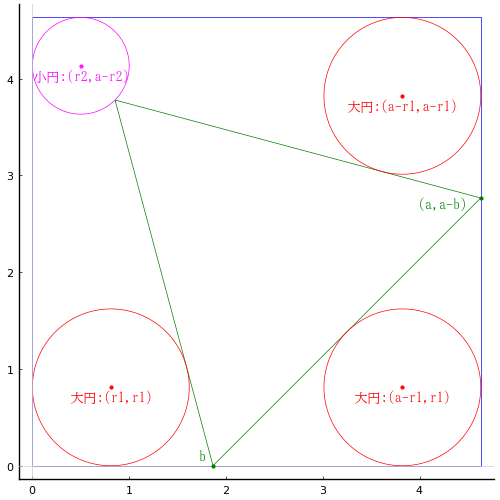
正方形の一辺の長さを a
正方形の辺上にある正三角形の頂点座標を (b, 0), (a, a - b)
大円の半径と中心座標を r1, (r1, r1), (a - r1, r1), (a - r1, a - r1)
小円の半径と中心座標を r2, (r2, a - r2)
とおき，以下の連立方程式を解く。

include("julia-source.txt")

using SymPy

@syms a::positive, b::positive, r1::positive, r2::positive
eq1 = √Sym(2)r1 + r1 + (a - b)√Sym(6)/2 + r2 + √Sym(2)r2 - √Sym(2)a
eq2 = 2(a - b) - (a - b)√Sym(2) - 2r1
eq3 = dist2(r2*(1 + √Sym(2))/√Sym(2), a - r2*(1 + √Sym(2))/√Sym(2), b, 0, r1, r1, r1);

まず，eq1, eq2 を解き a, b を求める。

res = solve([eq1, eq2], (a, b));

eq3 の a, b に，上で求めた a, b を代入する。方程式は分数式になるので，分子のみを使用する（分子 = 0 を解く）。

eq13 = eq3(a => res[a], b => res[b]) |> simplify |> numerator;

eq13 を r1 について解く（既知として与えられる r2 が含まれる式になる）。

ans_r1 = solve(eq13, r1)[1]
ans_r1 |> println

   r2*(-6081993113*sqrt(3) - 7322183923*sqrt(2) - 2*sqrt(-30721933218127447098*sqrt(3) - 37624610574115488280*sqrt(2) + 21722579043120417140*sqrt(6) + 53211949240534761996) + 4227464859*sqrt(6) + 10534321083)/(2*(-29290843252*sqrt(3) - 35584075994*sqrt(2) + 20544475854*sqrt(6) + 50733228709))

r2 にかかる係数は長精度実数演算が必要であるが，実数値 1.62035849881469 である。
上記のように r2* の形だと簡約化できないが係数部分だけを対象にすると簡約化できる。
この係数は「術」で述べられているものと同じである。

@syms d
z = ans_r1/r2
z = apart(z, d) |> factor
z |> println

   -(-9 - 5*sqrt(3) + 5*sqrt(2) + 3*sqrt(6))/2

a, b を求めるための r2 にかかる係数は以下のように求めることができる。

res[a](r1 => r2*z, r2 => 1).evalf() |> println

   9.26430077012849

res[b](r1 => r2*z, r2 => 1).evalf() |> println

   3.73205080756888

r2 が与えられると，r1, a, b は r2 の低数倍として以下のように計算できる。

(r1, a, b) = r2 .* [1.62035849881469, 9.26430077012849, 3.73205080756888];

小円の直径が 1 のとき，大円の直径は 1.62035849881469 である。

上述のように，「術」に述べられている式は，正しいものである。しかし，山村の解説では，最終的に「大径 = 小径×6.463284」となっているが，途中の式で「方斜率」を掛け忘れている。正しくは以下のように小径にかかる係数は 1.6203584988146877 である。

小径 = 1
方斜率 = √2
天 = √3
(天*5 + 9 - (天*3 + 5)*方斜率) * 小径 / 2

   1.6203584988146877

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r2 = 1/2
   (r1, a, b) = r2 .* [1.62035849881469, 9.26430077012849, 3.73205080756888]
   @printf("小円の直径が %g のとき，大円の直径は %g である。\n", 2r2, 2r1)
   @printf("r2 = %g;  r1 = %g;  a = %g;  b = %g\n", r2, r1, a, b)
   plot([0, a, a, 0, 0], [0, 0, a, a, 0], color=:blue, lw=0.5)
   plot!([r2*(1 + √2)/√2, b, a, r2*(1 + √2)/√2], [a - r2*(1 + √2)/√2, 0, a - b, a - r2*(1 + √2)/√2], color=:green, lw=0.5)
   circle(r1, r1, r1)
   circle(a - r1, r1, r1)
   circle(a - r1, a - r1, r1)
   circle(r2, a - r2, r2)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(r1, r1, "大円:(r1,r1)", :red, :center, delta=-delta/2)
       point(a - r1, r1, "大円:(a-r1,r1)", :red, :center, delta=-delta/2)
       point(a - r1, a - r1, "大円:(a-r1,a-r1)", :red, :center, delta=-delta/2)
       point(r2, a - r2, "小円:(r2,a-r2)", :magenta, :center, delta=-delta/2)
       point(b, 0, "b ", :green, :right, :bottom, delta=delta/2)
       point(a, a - b, "(a,a-b)  ", :green, :right, :vcenter, delta=-delta)
   end
end;