算額(その989)
一〇一 大宮市高鼻町 氷川神社 明治31年(1898)
埼玉県立図書館:埼玉県史料集 第二集『埼玉の算額』,昭和44年,誠美堂印刷所,埼玉県与野市.
外円の中に水平な弦を引き,区画された領域に大円 1 個,中円 2 個,小円 3 個を入れる。小円の直径が 1 寸のとき,中円の直径はいかほどか。
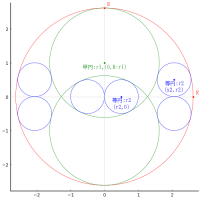
外円の半径と中心座標を R, (0, 0)
大円の半径と中心座標を r1, (0, R - r1)
中円の半径と中心座標を r2, (x2, y - r2); y = R - 2r1 + 2r3
小円の半径と中心座標を r3, (x3, y + r3)
とおき,以下の連立方程式を解く。
ただ,与えられた条件「小円の直径が 1 寸」だけでは答えが定まらない。
例えば,算額の図(『埼玉の算額』での図)では,中円と小円の中心の x 座標が等しいように描かれているので,「x3 = x2」という条件を加えて方程式を解くと以下のように,「中円の直径は 2 寸」という解が得られる。

include("julia-source.txt");
using SymPy
@syms R::poitive, r1::positive, r2::positive, x2::positive,
r3::positive, x3::positive
x3 = x2
y = R - 2r1 + 2r3
eq1 = x3^2 + (r1 - 3r3)^2 - (r1 + r3)^2
eq2 = x2^2 + (r1 - 2r3 + r2)^2 - (r1 + r2)^2
eq3 = x3^2 + (y + r3)^2 - (R - r3)^2
eq4 = x2^2 + (y - r2)^2 - (R - r2)^2
res = solve([eq1, eq2, eq3, eq4], (R, r1, r2, x2))
1-element Vector{NTuple{4, Sym{PyCall.PyObject}}}:
(6*r3, 3*r3, 2*r3, 4*r3)
function draw(more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
r3 = 1/2
(R, r1, r2, x2) = (6*r3, 3*r3, 2*r3, 4*r3)
x3 = x2
y = R - 2r1 + 2r3
plot()
circle(0, 0, R, :magenta)
circle(0, R - r1, r1)
circle2(x2, y - r2, r2, :green)
circle2(x3, y + r3, r3, :blue)
circle(0, R - 2r1 + r3, r3, :blue)
x = sqrt(R^2 - y^2)
segment(-x, y, x, y, :green)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:gray80, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
end
end;
draw(true)

「答」,「術」ともに小円の直径が 1 寸のとき,中円の直径は 1 寸 5 分としている。これがどのような状況下で得られる解なのか,「小円の直径と大円の直径の両方が与えられる」という条件のもとでの解を求める連立方程式を解くように修正してみる。
include("julia-source.txt");
using SymPy
@syms R::poitive, r1::positive, r2::positive, x2::positive,
r3::positive, x3::positive
y = R - 2r1 + 2r3
eq1 = x3^2 + (r1 - 3r3)^2 - (r1 + r3)^2
eq2 = x2^2 + (r1 - 2r3 + r2)^2 - (r1 + r2)^2
eq3 = x3^2 + (y + r3)^2 - (R - r3)^2
eq4 = x2^2 + (y - r2)^2 - (R - r2)^2;
res = solve([eq1, eq2, eq3, eq4], (R, r2, x2, x3))[2] # 2 of 2
(r1*(r1 - r3)/(r1 - 2*r3), r3*(r1 - r3)/(r1 - 2*r3), 2*sqrt(r3)*(r1 - r3)*sqrt(1/(r1 - 2*r3)), 2*sqrt(2)*sqrt(r3)*sqrt(r1 - r3))
解は 2 組得られるが,2 番目のものが敵解である。また,式中に平方根を計算する部分があり r1 > 2r3 という条件を満たさなければならないが,r1, r3 をいろいろ変化させてみると,求められた解に基づく図は,互いの円の内接・外接関係は題意を満たすものになっている。
結論:
算額の図のような解は,大円の直径が 3 のときに得られる。この場合,中円と小円の中心の x 座標が等しくなる。
算額の答,術のような解は,大円の直径が 4 のときに得られる。この場合,小円,中円が接する弦は外円の中心を通る(直径である)。
大円の直径が 1 より大きい値である限り,様々な見かけの図が得られる。
つまり,「条件として小円の直径を与えるだけでは,解は不定である」ということになる。
function draw(r3 = 1/2, r1 = 1.5, more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
(R, r2, x2, x3) = (r1*(r1 - r3)/(r1 - 2*r3), r3*(r1 - r3)/(r1 - 2*r3), 2*sqrt(r3)*(r1 - r3)*sqrt(1/(r1 - 2*r3)), 2*sqrt(2)*sqrt(r3)*sqrt(r1 - r3))
@printf("r3 = %g; r1 = %g; R = %g; r2 = %g; x2 = %g; x3 = %g\n", r3, r1, R, r2, x2, x3)
string = @sprintf("小円径 = %g\n大円径 = %g\n中円径 = %g", 2r3, 2r1, 2r2)
y = R - 2r1 + 2r3
plot()
circle(0, 0, R, :magenta)
circle(0, R - r1, r1)
circle2(x2, y - r2, r2, :green)
circle2(x3, y + r3, r3, :blue)
circle(0, R - 2r1 + r3, r3, :blue)
x = sqrt(R^2 - y^2)
segment(-x, y, x, y, :green)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:gray80, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
point(-R, R, string, :red, :left, mark=false)
point(0, R - r1, "大円:r1,(0,R-r1)", :red, :center, :bottom, delta=delta/2)
point(x2, y - r2, "中円:r2,(x2,y-r2)", :green, :center, delta=-delta/2)
point(x3, y + r3, "小円:r3\n(x3,y+r3)", :blue, :center, :center, delta=-delta/2)
end
end;
draw(0.5, 2, true)
r3 = 0.5; r1 = 2; R = 3; r2 = 0.75; x2 = 2.12132; x3 = 2.44949

draw(0.5, 3, true)
r3 = 0.5; r1 = 3; R = 3.75; r2 = 0.625; x2 = 2.5; x3 = 3.16228

draw(0.5, 1.2, true)
r3 = 0.5; r1 = 1.2; R = 4.2; r2 = 1.75; x2 = 2.21359; x3 = 1.67332