算額（その1064）

算額（その1064）

九十六 大船渡市立根 気仙安養寺稲荷堂 文政5年(1822)
山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市.
http://www.wasan.jp/yamamura/yamamura.html

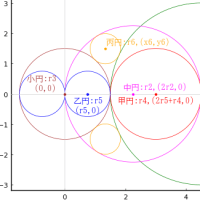
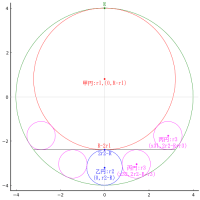
大円の中に，中円 1 個，小円 5 個を容れる。小円の直径が 1 寸のとき，大円の直径はいかほどか。なお，中円の直径は大円の半径に等しい。

大円の半径と中心座標を R, (0, 0); R = 2r1
中円の半径と中心座標を r1, (0, r1 - R)
小円の半径と中心座標を r2, (0, R - r2), (x21, y21), (x22, y22)
とおき，以下の連立方程式を解く。

include("julia-source.txt");

using SymPy
@syms R::positive, r1::positive, r2::positive,
     x21::positive, y21::positive,
     x22::positive, y22::negative
R = 2r1
eq1 = x21^2 + y21^2 - (R - r2)^2 |> expand
eq2 = x22^2 + y22^2 - (R - r2)^2 |> expand
eq3 = x22^2 + (y22 - r1 + R)^2 - (r1 + r2)^2 |> expand
eq4 = x21^2 + (R - r2 - y21)^2 - 4r2^2 |> expand
eq5 = (x22 - x21)^2 + (y21 - y22)^2 - 4r2^2 |> expand;

一度に解くことができないので，まずeq2, eq3, eq4, eq5 から x21, y21, x22, y22 を求める。

res = solve([eq2, eq3, eq4, eq5], (x21, y21, x22, y22))[2];
#= x22 =#  res[3] |> println
#= y22 =#  res[4] |> println

   2*sqrt(2)*sqrt(r2)*sqrt(r1 - r2)
   -2*r1 + 3*r2

式が簡単になる x22, y22 のみを採用し，連立方程式を組み直す（eq2, eq3 は意味を持たなくなるので除外）。

include("julia-source.txt");

using SymPy
@syms R::positive, r1::positive, r2::positive,
     x21::positive, y21::positive,
     x22::positive, y22::negative
R = 2r1
x22 = 2*sqrt(Sym(2))*sqrt(r2)*sqrt(r1 - r2)
y22 = -2*r1 + 3*r2
eq1 = x21^2 + y21^2 - (R - r2)^2 |> expand
eq4 = x21^2 + (R - r2 - y21)^2 - 4r2^2 |> expand
eq5 = (x22 - x21)^2 + (y21 - y22)^2 - 4r2^2 |> expand;

println(eq1, ",  # eq1")
println(eq4, ",  # eq4")
println(eq5, ",  # eq5")

   -4*r1^2 + 4*r1*r2 - r2^2 + x21^2 + y21^2,  # eq1
   4*r1^2 - 4*r1*r2 - 4*r1*y21 - 3*r2^2 + 2*r2*y21 + x21^2 + y21^2,  # eq4
   4*r1^2 - 4*r1*r2 + 4*r1*y21 - 4*sqrt(2)*sqrt(r2)*x21*sqrt(r1 - r2) - 3*r2^2 - 6*r2*y21 + x21^2 + y21^2,  # eq5

eq1, eq4, eq5 から，r1, x21, x22 を求める。

res2 = solve([eq1, eq4, eq5], (r1, x21, y21))[1]

   (r2*(CRootOf(x^3 - 2*x^2 + 2*x - 2, 0) + 2 + sqrt(CRootOf(x^3 - 2*x^2 + 2*x - 2, 0)^2 + 8))/4, r2*sqrt(-2*CRootOf(x^3 - 2*x^2 + 2*x - 2, 0)^2 + 8 + 2*sqrt(CRootOf(x^3 - 2*x^2 + 2*x - 2, 0)^2 + 8)*CRootOf(x^3 - 2*x^2 + 2*x - 2, 0))/2, r2*CRootOf(x^3 - 2*x^2 + 2*x - 2, 0))

(CRootOf(x^3 - 2*x^2 + 2*x - 2, 0) は x^3 - 2*x^2 + 2*x - 2 = 0 の実数解を得る関数である。具体的には 1.54368901269208 という数値である。

@syms x
term = sympy.CRootOf(x^3 - 2*x^2 + 2*x - 2, 0).evalf() |> println

   1.54368901269208

eq = x^3 - 2x^2 + 2x - 2
solve(eq)[3].evalf() |> println

   1.54368901269208

r2 が与えられたとき，以上をまとめて，r1, R, x21, y21, x22, y22 を求める手順を示す。

r2 = 1/2
term = 1.54368901269208
r1 = r2*(term + 2 + sqrt(term^2 + 8))/4
R = 2r1
x21 = r2*sqrt(-2*term^2 + 8 + 2*sqrt(term^2 + 8)*term)/2
y21 = r2*term
x22 = 2sqrt(2r2*(r1 - r2))
y22 = 3r2 - 2r1
(R, r1, x21, y21, x22, y22)

   (1.69148788395312, 0.84574394197656, 0.9076890632978463, 0.77184450634604, 1.175999901320676, -0.19148788395312)

中円の半径は，小円の半径の (term + 2 + sqrt(term^2 + 8))/4 = 1.69148788395312 倍，
大円の半径は，中円の半径の 2 倍である。
したがって，大円の半径は 小円の半径の 3.38297576790624 倍である。
小円の直径が 1 寸のとき，大円の直径は 3.38297576790624 寸である。

(term + 2 + sqrt(term^2 + 8))/4

   1.69148788395312

「術」も相当複雑なことをやっている。
結局数値解を求めることになってしまったので，最初から数値解を求めればよかった。

using NLsolve

function nls(func, params...; ini = [0.0])
   if typeof(ini) <: Number
       r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params..., [ini]), ftol=big"1e-40")
       v = r.zero[1]
   else
       r = nlsolve((vout, vin)->vout .= func(vin, params...), ini, ftol=big"1e-40")
       v = r.zero
   end
   return Float64.(v), r.f_converged
end;

function H(u)
   (r1, x21, y21, x22, y22) = u
   return [
       -4*r1^2 + 4*r1*r2 - r2^2 + x21^2 + y21^2,  # eq1
       -4*r1^2 + 4*r1*r2 - r2^2 + x22^2 + y22^2,  # eq2
       -2*r1*r2 + 2*r1*y22 - r2^2 + x22^2 + y22^2,  # eq3
       4*r1^2 - 4*r1*r2 - 4*r1*y21 - 3*r2^2 + 2*r2*y21 + x21^2 + y21^2,  # eq4
       -4*r2^2 + x21^2 - 2*x21*x22 + x22^2 + y21^2 - 2*y21*y22 + y22^2,  # eq5
   ]
end;

r2 = 1/2
iniv = BigFloat[10, 10, 15, 13, 2] ./ 10
res = nls(H, ini=iniv)

   ([0.8457439419765593, 0.907689063297846, 0.7718445063460382, 1.175999901320675, -0.19148788395311875], true)

小円の直径が 1 のとき，大円の直径は 3.38298 である。

その他のパラメータは以下のとおりである。

   r2 = 0.5;  r1 = 0.845744;  R = 1.69149;  x21 = 0.907689;  y21 = 0.771845;  x22 = 1.176;  y22 = -0.191488

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r2 = 1/2
   term = 1.54368901269208
   r1 = r2*(term + 2 + sqrt(term^2 + 8))/4
   R = 2r1
   x21 = r2*sqrt(-2*term^2 + 8 + 2*sqrt(term^2 + 8)*term)/2
   y21 = r2*term
   x22 = 2sqrt(2r2*(r1 - r2))
   y22 = 3r2 - 2r1
   @printf("小円の直径が %g のとき，大円の直径は %g である。\n", 2r2, 2R)
   @printf("その他のパラメータは以下のとおりである。\nr2 = %g;  r1 = %g;  R = %g;  x21 = %g;  y21 = %g;  x22 = %g;  y22 = %g\n", r2, r1, R, x21, y21, x22, y22)
   plot()
   circle(0, 0, R)
   circle(0, R - r2, r2, :blue)
   circle2(x21, y21, r2, :blue)
   circle2(x22, y22, r2, :blue)
   circle(0, r1 - R, r1, :green)
   if more        
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(0, R, " R", :green, :left, :bottom, delta=delta/2)
       point(0, r1 - R, "大円:r2,(0,r1-R)", :green, :center, delta=-delta/2)
       point(0, R - r2, "小円:r2,(0,R-r2)", :blue, :center, delta=-delta/2)
       point(x21, y21, "小円:r2,(x21,y21)", :blue, :center, delta=-delta/2)
       point(x22, y22, "小円:r2,(x22,y22)", :blue, :center, delta=-delta/2)
   end
end;