算額(その1047)
八十二 藤沢町保呂羽保呂羽山 保呂羽神社 明治7年(1874)
山村善夫:現存 岩手の算額,昭和52年1月30日,熊谷印刷,盛岡市.
http://www.wasan.jp/yamamura/yamamura.html
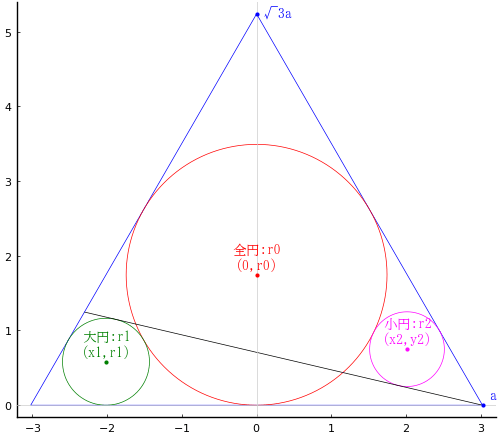
直線の上に小円 2 個が互いに接して載っている。その上に,小円を 3 個含む,交差する大円 2 個が載っている。
黒積(図で灰色に塗った面積)を求めよ。

手計算すればよいのだが,大円とy 軸の交点の y 座標を求める。
include("julia-source.txt");
using SymPy
@syms r1::positive, r2::negative, x::positive, y::positive
r1 = 2r2
eq1 = (x - r2)^2 + (y - 4r2)^2 - 4r2^2
solve(eq1, y)[2](x => 0) |> println
sqrt(3)*(-r2) + 4*r2
求める面積(黒積)は「台形OABC の面積から大円の面積の 1/12(OAD) と小円の面積の 1/4(CBD) を差し引いた面積の 2 倍」である。
# 台形OABC の面積
S1 = ((1 + (2 - √Sym(3))) + 3)/2*r2^2
S1 |> println
# 大円の面積の 1/12
S2 = PI*(2r2)^2/12
S2 |> println
# 小円の面積の 1/4
S3 = PI*r2^2/4
S3 |> println
r2^2*(3 - sqrt(3)/2)
pi*r2^2/3
pi*r2^2/4
小円の直径が 1 寸のときの黒積は -7*π/24 - sqrt(3)/4 + 3/2 = 0.150689440810758 である。
black = 2(S1 - S2 - S3)(r2 => 1//2)
black |> println
black.evalf() |> println
-7*pi/24 - sqrt(3)/4 + 3/2
0.150689440810758
function paintitblack(r2)
θ = 240:0.1:270
x = 2r2.*cosd.(θ) .+ r2
y = 2r2.*sind.(θ) .+ 4r2
θ2 = 90:0.1:180
append!(x, r2.*cosd.(θ2) .+ r2)
append!(y, r2.*sind.(θ2) .+ r2)
append!(x, -reverse(x))
append!(y, reverse(y))
append!(x, [0, 0])
append!(y, [r2, r2*(3 - √3)])
plot!(x, y, seriestype=:shape, fillcolor=:gray80)
end;
function draw(more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
r2 = 1/2
r1 = 2r2
plot(r2.*[1, 0, 0, 1, 1], r2.*[4, 4 - √3, 1, 1, 4], color=:black, lw=1)
circle2(r2, 4r2, r1)
circle(0, 4r2, r2, :blue)
circle2(r2, r2, r2, :blue)
circle2(2r2, 4r2, r2, :blue)
paintitblack(r2)
segment(-3r2, 0, 3r2, 0, :black, lw=1)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
#hline!([0], color=:gray80, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
point(r2, 4r2, "O ", :black, :right, :vcenter)
point(0, r2*(4 - √3), "A ", :black, :center, :bottom, delta=delta)
point(0, r2, "B ", :black, :right, :vcenter)
point(r2, r2, " C", :black, :left, :vcenter)
point(r2, 2r2, " D", :black, :left, :bottom, delta=delta)
point(0, 4*r2 - sqrt(3)*r2)
point(0, 4r2, "小円:r2,(0,4r2)", :blue, :center, :bottom, delta=delta)
point(r2, r2, "小円:r2,(r2,r2)", :blue, :center, delta=-delta)
point(r2, 4r2, " 大円:2r2,(r2,4r2)", :red, :left, :vcenter)
end
end;