算額(その343)
和算で遊ぼう!! 「三春まちなか寺子屋」2017レポート
https://miharukoma.com/wp-content/uploads/2018/01/%E4%B8%89%E6%98%A5%E3%81%BE%E3%81%A1%E3%81%AA%E3%81%8B%E5%AF%BA%E5%AD%90%E5%B1%8B2017%E3%83%AC%E3%83%9D%E3%83%BC%E3%83%88.pdf
10月 七草木天神社
長方形内に斜線を描き,甲円 1 個,乙円 2 個,丙円 1 個を入れる。乙円の直径が 9 寸のとき,丙円の直径を求めよ。
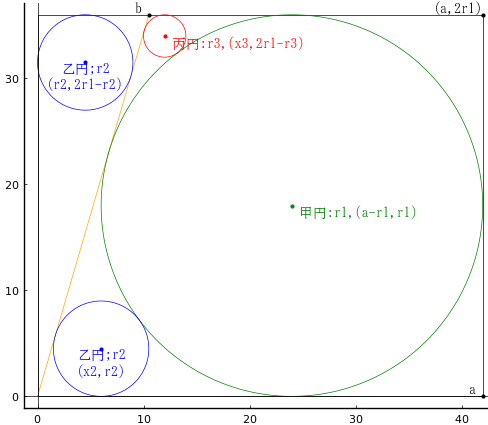
長方形の幅を a,斜線の端点の座標を (0, 0), (b, 2r1) とする。
甲円の半径,中心座標を r1, (a - r1, r1)
乙円の半径,中心座標を r2, (2r1 - r2), (x2, r2)
丙円の半径,中心座標を r3, (x3, 2r1 - r3)
とおき,以下の連立方程式を nlsole() で解き,数値解を求める。
include("julia-source.txt");
using SymPy
@syms a::positive, b::positive, r1::positive, r2::positive, x2::positive, r3::positive, x3::positive
@syms a, b, r1, r2, x2, r3, x3
@syms d
eq1 = (a - r1 - x3)^2 + (2r1 - r3 - r1)^2 - (r1 + r3)^2 |> expand |> simplify
eq2 = (a - r1 - x2)^2 + (r1 - r2)^2 - (r1 + r2)^2 |> expand |> simplify
eq3 = distance(0, 0, b, 2r1, r2, 2r1 - r2) - r2^2
eq4 = distance(0, 0, b, 2r1, x2, r2) - r2^2
eq5 = distance(0, 0, b, 2r1, x3, 2r1 - r3) - r3^2
eq6 = distance(0, 0, b, 2r1, a - r1, r1) - r1^2;
eq3 = apart(eq3, d) |> numerator |> expand |> simplify
eq4 = apart(eq4, d) |> numerator |> expand |> simplify
eq5 = apart(eq5, d) |> numerator |> expand |> simplify
eq6 = apart(eq6, d) |> numerator |> expand |> simplify;
println(eq1, ", # eq1")
println(eq2, ", # eq2")
println(eq3, ", # eq3")
println(eq4, ", # eq4")
println(eq5, ", # eq5")
println(eq6, ", # eq6")
a^2 - 2*a*r1 - 2*a*x3 + r1^2 - 4*r1*r3 + 2*r1*x3 + x3^2, # eq1
a^2 - 2*a*r1 - 2*a*x2 + r1^2 - 4*r1*r2 + 2*r1*x2 + x2^2, # eq2
4*b*r1*(b*r1 - b*r2 - 2*r1*r2 + r2^2), # eq3
4*r1*(-b*r2*x2 - r1*r2^2 + r1*x2^2), # eq4
4*r1*(b^2*r1 - b^2*r3 - 2*b*r1*x3 + b*r3*x3 - r1*r3^2 + r1*x3^2), # eq5
4*r1^2*(a^2 - a*b - 2*a*r1 + b*r1), # eq6
using NLsolve
function nls(func, params...; ini = [0.0])
if typeof(ini) <: Number
r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params..., [ini]), ftol=1e-14)
v = r.zero[1]
else
r = nlsolve((vout, vin)->vout .= func(vin, params...), ini, ftol=1e-14)
v = r.zero
end
return v, r.f_converged
end;
function H(u)
(a, b, r1, x2, r3, x3) = u
return [
a^2 - 2*a*r1 - 2*a*x3 + r1^2 - 4*r1*r3 + 2*r1*x3 + x3^2, # eq1
a^2 - 2*a*r1 - 2*a*x2 + r1^2 - 4*r1*r2 + 2*r1*x2 + x2^2, # eq2
4*b*r1*(b*r1 - b*r2 - 2*r1*r2 + r2^2), # eq3
4*r1*(-b*r2*x2 - r1*r2^2 + r1*x2^2), # eq4
4*r1*(b^2*r1 - b^2*r3 - 2*b*r1*x3 + b*r3*x3 - r1*r3^2 + r1*x3^2), # eq5
4*r1^2*(a^2 - a*b - 2*a*r1 + b*r1), # eq6
]
end;
r2 = 9//2
iniv = [big"40.0", 10, 20, 5, 2, 10]
res = nls(H, ini=iniv);
println(res);
(BigFloat[42.00000000000000000000000000000000002256826092573487185561562244382886438918157, 10.49999999999999999999999999999999999460987895327460597548276631046112533791355, 18.00000000000000000000000000000000001793984185362760822286679887253225521134492, 5.999999999999999999999999999999999994624492660452202698353623697006093101679257, 1.999999999999999999999998432434804260885043360258691473226485827072352597107708, 12.00000000000000000000000313847108063424084221460499189708023376629061330011589], true)
a = 42; b = 10.5; r1 = 18; x2 = 6; r3 = 2; x3 = 12
丙円の直径(2r3) = 4
function draw(more)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
r2 = 9//2
(a, b, r1, x2, r3, x3) = res[1]
@printf("r2 = %g; a = %g; b = %g; r1 = %g; x2 = %g; r3 = %g; x3 = %g\n", r2, a, b, r1, x2, r3, x3)
@printf("丙円の直径(2r3) = %g\n", 2r3)
plot([0, a, a, 0, 0], [0, 0, 2r1, 2r1, 0], color=:black, lw=0.5)
segment(0, 0, b, 2r1, :orange)
circle(a - r1, r1, r1, :green)
circle(r2, 2r1 - r2, r2, :blue)
circle(x2, r2, r2, :blue)
circle(x3, 2r1 - r3, r3)
if more
point(a, 0, "a ", :black, :right, :bottom)
point(b, 2r1, "b ", :black, :right, :bottom)
point(a, 2r1, "(a,2r1)", :black, :right, :bottom)
point(a - r1, r1, " 甲円:r1,(a-r1,r1)", :green)
point(r2, 2r1 - r2, "乙円;r2\n(r2,2r1-r2)", :blue, :center)
point(x2, r2, "乙円;r2\n(x2,r2)", :blue, :center)
point(x3, 2r1 - r3, " 丙円:r3,(x3,2r1-r3)", :red)
hline!([0], color=:black, lw=0.5)
vline!([0], color=:black, lw=0.5)
else
plot!(showaxis=false)
end
end;