算額（その341）

算額（その341）

和算で遊ぼう！！ 「三春まちなか寺子屋」2017レポート
https://miharukoma.com/wp-content/uploads/2018/01/%E4%B8%89%E6%98%A5%E3%81%BE%E3%81%A1%E3%81%AA%E3%81%8B%E5%AF%BA%E5%AD%90%E5%B1%8B2017%E3%83%AC%E3%83%9D%E3%83%BC%E3%83%88.pdf

7月 高木神社
長方形の中に，春円 1 個，夏円 2 個，秋円 1 個，冬円 1 個を入れる。5 個の円の直径の和が 8 寸のとき，長方形の縦の長さ（春円の直径）を求めよ。

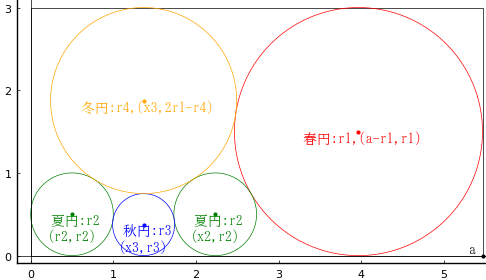
春円の半径，中心座標を r1, (a - r1, r1)
夏円の半径，中心座標を r2, (x2, r2), (r2, r2)
秋円の半径，中心座標を r3, (x3, r3)
冬円の半径，中心座標を r4, (x3, 2r1 - r4)
とおき，以下の連立方程式を解く。

include("julia-source.txt");

using SymPy

@syms a::positive, r1::positive, r2::positive, x2::positive, r3::positive, x3::positive, r4::positive

eq1 = r1 + 2r2 + r3 + r4 - 8//2
eq2 = (a - r1 - x2)^2 + (r1 - r2)^2 - (r1 + r2)^2 |> expand
eq3 = (a - r1 - x3)^2 + (r4 - r1)^2 - (r1 + r4)^2 |> expand
eq4 = (x2 - x3)^2 + (r2 - r3)^2 - (r2 + r3)^2 |> expand
eq5 = (x2 - x3)^2 + (2r1 - r4 - r2)^2 - (r2 + r4)^2 |> expand
eq6 = (x3 - r2)^2 + (r2 - r3)^2 - (r2 + r3)^2 |> expand
eq7 = r3 + r4 - r1;

res = solve([eq1, eq2, eq3, eq4, eq5, eq6, eq7], (a, r1, r2, x2, r3, x3, r4))

   2-element Vector{NTuple{7, Sym}}:
    (2 - sqrt(3), 3/2, 1/2, 1/2, 3/8, 1/2 + sqrt(3)/2, 9/8)
    (2 + 2*sqrt(3), 3/2, 1/2, 1/2 + sqrt(3), 3/8, 1/2 + sqrt(3)/2, 9/8)

   a = 5.4641;  r1 = 1.5;  r2 = 0.5;  x2 = 2.23205;  r3 = 0.375;  x3 = 1.36603;  r4 = 1.125
   春円の直径 = 3;  夏円の直径 = 1;  秋円の直径 = 0.75;  冬の直円径 = 2.25
   長方形の縦の長さ = 春円の直径 = 3

function draw(more)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (a, r1, r2, x2, r3, x3, r4) = res[2]
   @printf("a = %g;  r1 = %g;  r2 = %g;  x2 = %g;  r3 = %g;  x3 = %g;  r4 = %g\n", a, r1, r2, x2, r3, x3, r4)
   @printf("春円の直径 = %g;  夏円の直径 = %g;  秋円の直径 = %g;  冬の直円径 = %g\n", 2r1, 2r2, 2r3, 2r4)
   @printf("長方形の縦の長さ = 春円の直径 = %g\n", 2r1)
   plot([0, a, a, 0, 0], [0, 0, 2r1, 2r1, 0], color=:black, lw=0.5)
   circle(a - r1, r1, r1)
   circle(x2, r2, r2, :green)
   circle(r2, r2, r2, :green)
   circle(x3, r3, r3, :blue)
   circle(x3, 2r1 - r4, r4, :orange)
   if more
       point(a - r1, r1, " 春円:r1,(a-r1,r1)", :red, :center)
       point(x2, r2, " 夏円:r2\n(x2,r2)", :green, :center)
       point(r2, r2, " 夏円:r2\n(r2,r2)", :green, :center)
       point(x3, r3, " 秋円:r3\n(x3,r3)", :blue, :center)
       point(x3, 2r1 - r4, " 冬円:r4,(x3,2r1-r4)", :orange, :center)
       point(a, 0, "a ", :black, :right, :bottom)
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5)
   else
       plot!(showaxis=false)
   end
end;

 

 

算額（その340）

算額（その340）

和算で遊ぼう！！ 「三春まちなか寺子屋」2017レポート
https://miharukoma.com/wp-content/uploads/2018/01/%E4%B8%89%E6%98%A5%E3%81%BE%E3%81%A1%E3%81%AA%E3%81%8B%E5%AF%BA%E5%AD%90%E5%B1%8B2017%E3%83%AC%E3%83%9D%E3%83%BC%E3%83%88.pdf

5月 愛宕神社

求めるものは違うが，算額（その142）「三重県四日市市 神明神社 寛政2年」と基本的に同じ。

乾円，坤円の直径がそれぞれ 4 寸，1 寸のとき，地円の直径を求めよ。

なお，乾円の直径と坤円の直径がある値より大きくなれば，鉤が股より大きくなる。算額のような，乾円径 = 4, 坤円径 = 1 の場合だと，算額の図とは異なるイメージのものになる。

上図のように記号を定め，式を立て，解く。solve() ではなく，nlsolve() による。

連立方程式の段階では r4，r5 は記号として扱う。

include("julia-source.txt");

using SymPy

@syms r1, r2, r3, x2, x3, x4, x5, x, y
@syms r4, r5

eq1 = (x2 - r1)^2 + (r1 - r2)^2 - (r1 + r2)^2 |> expand  # 天地
eq2 = (x3 - x2)^2 + (r2 - r3)^2 - (r2 + r3)^2 |> expand  # 地人
eq3 = (x4 - r1)^2 + (r1 - r4)^2 - (r1 + r4)^2 |> expand  # 天乾
eq4 = (x2 - x4)^2 + (r2 - r4)^2 - (r2 + r4)^2 |> expand  # 地乾
eq5 = (x5 - x2)^2 + (r2 - r5)^2 - (r2 + r5)^2 |> expand  # 地坤
eq6 = (x3 - x5)^2 + (r3 - r5)^2 - (r3 + r5)^2 |> expand  # 人坤
eq7 = r1*(x + y + sqrt(x^2 + y^2)) - x*y |> expand  # 直角三角形の面積
eq8 = r1*(x - x2) - r2*(x - r1) |> expand  # 半径の関係（三角形の相似）
eq9 = r1*(x - x3) - r3*(x - r1) |> expand; # 半径の関係（三角形の相似）

println(eq1, ", # eq1")
println(eq2, ", # eq2")
println(eq3, ", # eq3")
println(eq4, ", # eq4")
println(eq5, ", # eq5")
println(eq6, ", # eq6")
println(eq7, ", # eq7")
println(eq8, ", # eq8")
println(eq9, ", # eq9")

   r1^2 - 4*r1*r2 - 2*r1*x2 + x2^2, # eq1
   -4*r2*r3 + x2^2 - 2*x2*x3 + x3^2, # eq2
   r1^2 - 4*r1*r4 - 2*r1*x4 + x4^2, # eq3
   -4*r2*r4 + x2^2 - 2*x2*x4 + x4^2, # eq4
   -4*r2*r5 + x2^2 - 2*x2*x5 + x5^2, # eq5
   -4*r3*r5 + x3^2 - 2*x3*x5 + x5^2, # eq6
   r1*x + r1*y + r1*sqrt(x^2 + y^2) - x*y, # eq7
   r1*r2 + r1*x - r1*x2 - r2*x, # eq8
   r1*r3 + r1*x - r1*x3 - r3*x, # eq9

using NLsolve

function nls(func, params...; ini = [0.0])
   if typeof(ini) <: Number
       r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params..., [ini]))#, ftol=1e-14)
       v = r.zero[1]
   else
       r = nlsolve((vout, vin)->vout .= func(vin, params...), ini)#, ftol=1e-14)
       v = r.zero
   end
   return v, r.f_converged
end;

function H(u)
   (r1, r2, r3, x2, x3, x4, x5, x, y) = u
   return [
       r1^2 - 4*r1*r2 - 2*r1*x2 + x2^2, # eq1
       -4*r2*r3 + x2^2 - 2*x2*x3 + x3^2, # eq2
       r1^2 - 4*r1*r4 - 2*r1*x4 + x4^2, # eq3
       -4*r2*r4 + x2^2 - 2*x2*x4 + x4^2, # eq4
       -4*r2*r5 + x2^2 - 2*x2*x5 + x5^2, # eq5
       -4*r3*r5 + x3^2 - 2*x3*x5 + x5^2, # eq6
       r1*x + r1*y + r1*sqrt(x^2 + y^2) - x*y, # eq7
       r1*r2 + r1*x - r1*x2 - r2*x, # eq8
       r1*r3 + r1*x - r1*x3 - r3*x, # eq9
   ]
end;

(r4, r5) = (4, 1) .// 2  # r4, r5 に数値を代入
iniv = [big"40.0", 25, 18, 101, 145, 72, 125, 230, 95]
res = nls(H, ini=iniv)
println(res);
   (BigFloat[17.99999999999999999999959359538046894328544006940578449319282835040346165571312, 4.500000000000000000000021850969763478122224875168800267359829481564552397400594, 1.125000000000000000000015511954584626415427036519923717249791558076525292630489, 35.99999999999999999999950081078087049912383423570819427141543308984033365075256, 40.49999999999999999999954859392954415808055400655154524243081491576853407899673, 29.99999999999999999999948510964983470350422331631829474897253215082231657323331, 38.99999999999999999999950866369699465815370090785716009867301337616840188238613, 41.99999999999999999999957349741006947409069773160858398799318001605314871943797, 143.9999999999999993599636251260970577496755779165141698135744945781538654670987], true)

   鉤 = 144;  股 = 42
   天円径 = 36;  地円径 = 9;  人円径 = 2.25
   乾円径 = 4;  坤円径 = 1

地円の半径 = 4.5。元の単位では，直径 9 寸。

なお，術では「乾円径と坤円径の積の平方根を2倍したものに乾円径と坤円径を加える」とのこと。
2sqrt(4 * 1) + 4 + 1 = 9

2sqrt(4 * 1) + 4 + 1

   9.0

using Plots

function draw(more)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (r1, r2, r3, x2, x3, x4, x5, x, y) = res[1]
   @printf("鉤 = %g;  股 = %g\n", y, x)
   @printf("天円径 = %g;  地円径 = %g;  人円径 = %g\n", 2r1, 2r2, 2r3)
   @printf("乾円径 = %g;  坤円径 = %g\n", 2r4, 2r5)
   plot([0, x, 0, 0], [0, 0, y, 0], color=:black, lw=0.5)
   circle(r1, r1, r1)
   circle(x2, r2, r2, :blue)
   circle(x3, r3, r3, :magenta)
   circle(x4, r4, r4, :orange)
   circle(x5, r5, r5, :green)
   if more == true
       point(r1, r1, "天:(r1,r1)", :red, :center, :bottom)
       point(x2, r2, "地:(x2,r2)", :blue, :center, :bottom)
       point(x3, r3, "人:(x3,r3)", :magenta, :center, :bottom)
       point(x4, r4, "乾:(x4,r4)", :orange, :center, :bottom)
       point(x5, r5, "坤:(x5,r5)", :green, :center, :bottom)
       # point(0, y, " y", :black, :left, :bottom)
       point(x, 0, " x", :black, :left, :bottom)
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5)
       plot!(xlims=(-2, 45), ylims=(-2, 20))
   else
       plot!(showaxis=false)
   end
end;