算額（その324）

算額（その324）

早坂平四郎:算額の一考察，苫小牧工業専門学校紀要
https://www.tomakomai-ct.ac.jp/wp01/wp-content/uploads/2014/06/kiyou5-8.pdf

四分円に関するもの
千葉県成田市 成田不動新勝寺光明堂 明治30年(1897)

元の算額では第一象限のみにいて書いているが，その限定は不要なので全体について述べる。
外円の中に，大円 4 個，中円 4 個，小円 4 個を入れる。図のように，中円は大円の交差する領域に，小円は 2 個の大円と外円に接する。小円の直径を中円の直径で表わせ。

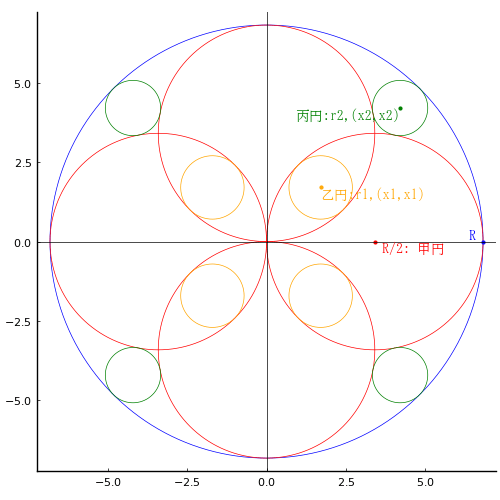
大円の半径，中心座標を R, (0, 0)
右側の大円の半径，中心座標を R/2, (R/2, 0)
第一象限にある中円の半径，中心座標を r1, (x1, x1), x1 = R/4
第一象限にある小円の半径，中心座標を r2, (x2, x2)
とし，r1 は未知数のまま，以下の連立方程式を r2, x2, R について解く。

include("julia-source.txt");

using SymPy

@syms R::positive, r1::positive, x1::positive, r2::positive, x2::positive;
r1 = 1
x1 = R/4
eq1 = (R/4)^2 + x1^2 - (R/2 - r1)^2
eq2 = 2x2^2 - (R - r2)^2
eq3 = (x2 - R/2)^2 + x2^2 - (R/2 + r2)^2
res = solve([eq1, eq2, eq3], (r2, x2, R));
res |> println

   Tuple{Sym, Sym, Sym}[(2*r1*(-5*sqrt(2) - 4*sqrt(3 - 2*sqrt(2)) + 10)/17, 4*r1*(2 - sqrt(2))/17 + 24*r1*sqrt(3 - 2*sqrt(2))/17, 2*r1*(2 - sqrt(2))), (2*r1*(-5*sqrt(2) + 4*sqrt(3 - 2*sqrt(2)) + 10)/17, -24*r1*sqrt(3 - 2*sqrt(2))/17 + 4*r1*(2 - sqrt(2))/17, 2*r1*(2 - sqrt(2))), (2*r1*(5*sqrt(2) + 4*sqrt(2*sqrt(2) + 3) + 10)/17, -24*r1*sqrt(2*sqrt(2) + 3)/17 + 4*r1*(sqrt(2) + 2)/17, 2*r1*(sqrt(2) + 2)), (2*r1*(-4*sqrt(2*sqrt(2) + 3) + 5*sqrt(2) + 10)/17, 4*r1*(sqrt(2) + 2)/17 + 24*r1*sqrt(2*sqrt(2) + 3)/17, 2*r1*(sqrt(2) + 2))]

4 組目のものが適解である。

res[4]

   (2*r1*(-4*sqrt(2*sqrt(2) + 3) + 5*sqrt(2) + 10)/17, 4*r1*(sqrt(2) + 2)/17 + 24*r1*sqrt(2*sqrt(2) + 3)/17, 2*r1*(sqrt(2) + 2))

それぞれを簡約化する。

res[4][1] |> sympy.sqrtdenest |> simplify |> println  # r2

   2*r1*(sqrt(2) + 6)/17

丙円の直径は乙円の直径の 2(√2 + 6)/17 倍である。

res[4][2] |> sympy.sqrtdenest |> simplify |> println  # x2

   4*r1*(8 + 7*sqrt(2))/17

res[4][3] |> simplify |> println  # R

   2*r1*(sqrt(2) + 2)

using Plots

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r1 = 1
   r2 = 2*r1*(sqrt(2) + 6)/17
   x2 = 4*r1*(8 + 7*sqrt(2))/17
   R = 2*r1*(sqrt(2) + 2)
   x1 = R/4
   plot()
   circle(0, 0, R, :blue)
   circle42(0, R/2, R/2)
   circle4(x1, x1, r1, :orange)
   circle4(x2, x2, r2, :green)
   if more
       point(R, 0, "R ", :blue, :right, :bottom)
       point(R/2, 0, " R/2: 甲円", :red)
       point(x1, x1, "乙円:r1,(x1,x1)", :orange)
       point(x2, x2, "丙円:r2,(x2,x2)", :green, :right)
       vline!([0], color=:black, lw=0.5)
       hline!([0], color=:black, lw=0.5)
   else
       plot!(showaxis=false)
   end
end;

算額（その323）

算額（その323）

早坂平四郎:算額の一考察
https://www.tomakomai-ct.ac.jp/wp01/wp-content/uploads/2014/06/kiyou5-8.pdf

長方形に関するもの
千葉県千葉市千葉寺 千葉寺 明治30年(1897)

外円内に長方形を入れ，対角線を引く。区切られた領域に 6 個の等円を入れる。外円の直径は等円の直径の何倍か。

外円の半径を R，等円の半径を r とおき，長方形内の等円の一個から対角線までの距離が等円の半径に等しいという方程式を解く。

include("julia-source.txt");

using SymPy

@syms R::positive, r::positive;
eq1 = distance(0, 0, R - 2r, sqrt(R^2 - (R - 2r)^2), R - 3r, r) - r^2;
res = solve(eq1, (R));
res |> println

   Sym[2*r, 5*r, r*(5/2 - sqrt(5)/2)]

2 番目のものが適解。すなわち，外円の直径は等円の直径の 5 倍である。

using Plots

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r = 1
   R = 5r
   @printf("外円の径 = %.6f * 内円の径\n", R)
   plot()
   circle(0, 0, R, :blue)
   circle(R - r, 0, r)
   circle(r - R, 0, r)
   circle4(R - 3r, r, r)
   x = R - 2r
   y = sqrt(R^2 - (R - 2r)^2)
   rect(-x, -y, x, y, :green)
   segment(-x, -y, x, y, :green)
   segment(-x, y, x, -y, :green)
   if more
       point(R, 0, " R", :blue)
       point(R - r, 0, " R-r", :red)
       point(R - 2r, 0, " R-2r", :red)
       point(R - 3r, r, "\n(R-3r,r)", :red, :center)
       point(0, sqrt(R^2 - (R - 2r)^2), " √(R^2-(R-2r)^2)")
       vline!([0], color=:black, lw=0.5)
       hline!([0], color=:black, lw=0.5)
   else
       plot!(showaxis=false)
   end
end;