算額(その334)
遠藤寛子:「算法少女」
https://www.chikumashobo.co.jp/product/9784480090133/
久留米藩の殿様の有馬頼徸が,千葉あきと中根宇多に出した問題。
『円のうちに,大円二個,小円二個が接した形があるが,それらの大円小円は,またおたがいに接している。いま,いちばん外側の円の直径を七寸,内に接している大きい方の円の直径を三寸としたら,小円の直径はいかほどか』
図は示されていないが以下のようなものを考えた。

include("julia-source.txt");
using SymPy
@syms r::positive, r1::positive, y1::positive, r2::positive, y2::negative;
(r, r1) = (7//2, 3//2)
eq1 = (r1 - r2)^2 + (y1 - y2)^2 - (r1 + r2)^2
eq2 = r1^2 + y1^2 - (r - r1)^2
eq3 = r2^2 + y2^2 - (r - r2)^2
res1 = solve([eq1, eq2, eq3], (r2, y1, y2))
1-element Vector{Tuple{Sym, Sym, Sym}}:
(21*sqrt(14)/169 + 315/338, (7 + 6*sqrt(14))*sqrt(79 - 12*sqrt(14))/130, -7*sqrt(79/676 - 3*sqrt(14)/169))
小円の半径は 1.39689233800150 で,元の単位での直径は 2寸7分9厘3毛7糸...である。
あきの出した答えは「2寸8分」。きれいな数値だ。
res1[1][1].evalf() |> println
1.39689233800150
1.39689233800150*2
2.793784676003
y1, y2 は二重根号を外すと簡約化できる。
res1[1][2] |> sympy.sqrtdenest |> simplify |> println
sqrt(7)/2
res1[1][3] |> sympy.sqrtdenest |> simplify |> println
-21*sqrt(2)/13 + 7*sqrt(7)/26
using Plots
function draw(more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
(r, r1) = (7//2, 3//2)
(r2, y1, y2) = ((42*sqrt(14) + 315)/338, sqrt(7)/2, (7*sqrt(7) - 42*sqrt(2))/26)
@printf("小円の直径 = %.6f\n", 2r2)
plot()
circle(0, 0, r)
circle(r1, y1, r1, :blue)
circle(-r1, y1, r1, :blue)
circle(r2, y2, r2, :orange)
circle(-r2, y2, r2, :orange)
if more
point(r1, y1, "大円:r1\n(r1,y1)", :blue)
point(r2, y2, "小円:r2\n(r2,y2)", :orange)
point(r, 0, "r ", :red, :right)
vline!([0], color=:black, lw=0.5)
hline!([0], color=:black, lw=0.5)
else
plot!(showaxis=false)
end
end;
ネットを散策して,もう一つの図の可能性がわかった。映画版では以下のような図が示されていたとのこと。
街角の数学
http://streetwasan.web.fc2.com/math17.12.13.html
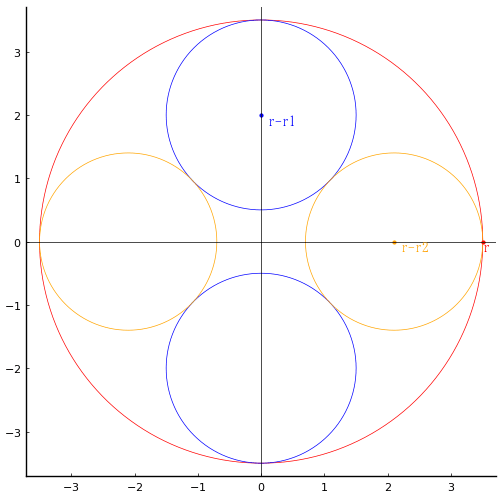
こちらは,大円,小円の中心が x 軸,y 軸上にあるので非常に簡単で eq は 10r2 = 14 になり爆速で答えが出る(お話にならない)。しかもきれいな数値で,あきが答えた通り,直径は 2.8 = 2寸8 分である。
しかし,有馬の殿様がこんな簡単な問題を出したとは思えない。やはり,最初の図のほうが解きがいがあるのでは?
using SymPy
@syms r, r1, r2
(r, r1) = (7//2, 3//2)
eq = (r - r1)^2 + (r - r2)^2 - (r1 + r2)^2 |> expand
eq |> println
solve(eq)[1] |> println
14 - 10*r2
7/5
using Plots
function draw(more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
(r, r1) = (7//2, 3//2)
r2 = 7/5
@printf("小円の直径 = %.6f\n", 2r2)
plot()
circle(0, 0, r)
circle(0, r - r1, r1, :blue)
circle(0, r1 - r, r1, :blue)
circle(r - r2, 0, r2, :orange)
circle(r2 - r, 0, r2, :orange)
if more
point(0, r - r1, " r-r1", :blue)
point(r - r2, 0, " r-r2", :orange)
point(r, 0, "r ", :red)
vline!([0], color=:black, lw=0.5)
hline!([0], color=:black, lw=0.5)
else
plot!(showaxis=false)
end
end;



















