大げさなタイトルになりましたが、2桁の数の掛け算の暗算方法について、方法論を提示したいと思います。
まぁ、本当の究極の暗算法は丸暗記することかもしれませんが、それは置いておきまして。。
何故、そこまで言えるのかと申しますと、テーマが単純で手を入れる要素も少ないので、自分よりもっと頭のいい人が考えたとしても
これ以上先はもう無いだろう、と考えるからです。
この項は前半は理論であり、後半は具体的方法です。面倒くさい人は後半のみお読み下さい。
また、内容的には前回の記事の続きでもあるので、前回の記事も併せて読まれることをお勧めします。
まあ、私などが申すべくもなく、ネット等で検索するれば色々なものが出てきます。
その中には、ほとんど自分の考えたものと同じものも多々ありました。というか、考えている人は程んど同じ結論に達するのでしょう。
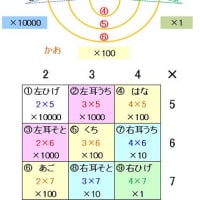
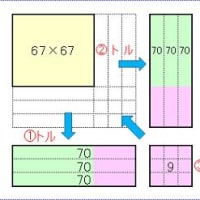
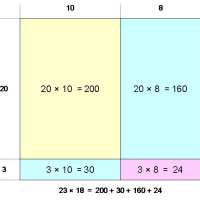
その同じ結論というのは、掛け算を4つの四角形の面積でかんがえるというやり方です。
たとえば 78×63 という計算なら以下のような四角形を考える。
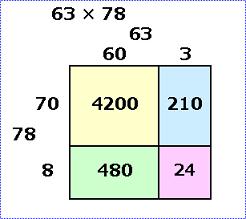
これは計算のイメージとしては基本のものであり、理解しやすいと思います。
かつ子供に教えてもその後の数学的な思考展開の基礎となるものであり、意義のあることと考えます。
それでこの4つの四角形を足し上げて掛け算の答えを出すというものです。
つまり 4200+480+210+24
で、いくつになるかな 4914 ですな。
この四角形ををイメージしながら足し上げれば何とか暗算は出来るわけで、前回の4つの数の足し算をするという
内容と軌を一にします。
ただし、自分は時々単純計算であっても、「あれっ?」となってしまうタイプなので、それでもきつい場合がある。
もうちょっと工夫できないか。
工夫もなにも足し算する順番を考えるだけなのですが、色々と試行錯誤した結果、
四角形のうち右上と左下、この斜めのラインの合計を一番先に出すのが良いと考えました。
すなわち上記の例では 480+210 = 690 この計算を先ずやってしまう。
ここで 480 と 210 は 10の倍数になっていることに注意します。
その次に、左上、すなわち4200、100の倍数の数を足す。4890になる。
そして最後に右下の数、24という単純な九九の数を足す。 答えは 4914。
何故この順番なのか?
それは一つには各項を足し上げていくときに、
「先ずは、数字の桁の重なりが多いもの同士を最初に足してしまおう」 という考え方なんです。
つまり、480と210は10の倍数同士。これを先ずまとめてしまえ、ということです。
この場合は繰り上がりこそおきないものの、足し算するけたは100の位と10の位、
2つの桁でばっちりぶつかりあう。だからここでまず 690 という数をつくり10の倍数の合計を固めてしまう。
そこであとから4200を足し、24を足しという風にすれば、以降は足し算する桁が1桁しか重ならない。
(ただし、10の倍数の合計が1000を超えた場合は2桁重なることもある。)
この順番を変えると、どうなるか。
例えば 4200+480 = 4680 と先にやり、4680と210を次に足そうとすると
この2桁がぶつかりあうという最もこの足し算で過酷な部分で、最初に10の倍数同士を足した場合よりも大きな数を扱うことになる。
もう一つ、480+210を先ず行うというのは、これはゼロを除いて考えると両方とも九九の答えであり、
よく見なれた数字であるということであるからです。
ある意味既知の数であり、ある種計算にも慣れているその分心理的にも抵抗が少なく、速く計算出来る。
だからこそ、2桁の数がぶつかりあう足し算をここで行うのです。
これは実際、訓練を重ねていくと、きわめて限られた数字を扱っているのだと気付きます。
つまりは「九九の答え同士の足し算」なわけで、パターンとして限られてくるのです。
よって、だんだん慣れてくるということです。
要は間違っても 470+760 なんていう足し算はでてこないということですね。
もう一度まとめてみます
最初に10の倍数同士を足した場合
手順1: 480+210 = 690 → 二桁がぶつかりあう足し算だが、見なれた数字なので心理的抵抗小
手順2: 690+4200=4890 → 見なれぬ数字(690)を含むが、足し算する桁は1桁のみで心理的抵抗小
手順3: 4890+24 =4914 → 見なれぬ数字(4890)を含むが、足し算する桁は1桁のみで心理的抵抗小
順番を変えた場合
手順1: 4200+480=4680 → 見なれた数字なので心理的抵抗小
手順2: 4680+210=4890 → 見なれぬ数字(4680)を含み、足し算する桁も2桁であり、心理的抵抗大
手順3: 4890+24 =4914 → 見なれぬ数字(4890)を含むが、足し算する桁は1桁のみで心理的抵抗小
さらに、この順番が良いと考えるもう一つの理由があります。
それは、最初に作る10の倍数の項の合計が、たまたま100の倍数になることがあるということです。
これが100の倍数になった場合は、以降、下二桁の計算はあってないようなものです。
つまりこれがインド式計算のパターンに当たる場合の83×87などでは、4つの四角形の左下・右上の合計が800となる。
だからその後の足し算が楽になる、ということは前回述べました。
しかし、ここで注目したいのは、10の倍数の項の合計が100の倍数になるというパターンは、
インド式計算のパターンに当てはまる計算式だけではなく、他にも数多くあるということなんです。
例えば、64×77 = 4200+280+420+28
これは 最初に 280と420を足してしまえばあとは楽ですね。 4200+700+28 = 4928
あるいは 92×86 などもそうでしょうか。
7200+540+160+12 = 7200+700+12 = 7912 となりますね。
これは二桁同士の掛け算の計算パターンの3321通りのうち、401通りがそうなります。ちょっとした数です。
※3321通りというのは最初の記事でもふれましたが、二桁同士の掛け算のうち、1の位がゼロのものを除き、
さらにかけられる数とかける数を入れ替えたものを相殺したネットの計算式のパターンです。
よって、4つの四角形の各項のうち、まず、左下・右下の10の倍数の項を足すのが良いというのは御理解いただけたと思います。
そのあと、100の倍数の項、単純九九の項という順で足す、というのが私の提案する順序です。
この点については、残念ながら理屈はありません。
ただ、実際多くの計算にあたった結果、感覚的にこれが良いという結論に達しています。
以上が理論ですが、最後に具体的な方法論に入りたいと思います。
 究極の2桁掛け算暗算法
究極の2桁掛け算暗算法 :
:
計算方法を具体化する際に、以上説明してきた「10の倍数の数の合計を出す」方法に関して
一つ変更を加えます。それは、「先ず九九の答え同士を足し、後から10倍する」ということです。
(同じことですよね)
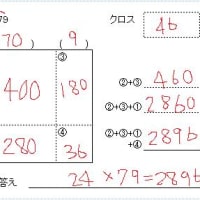
それを踏まえて、例えば、78×63 という計算なら、
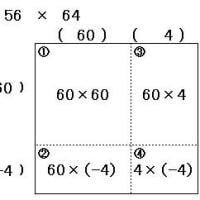
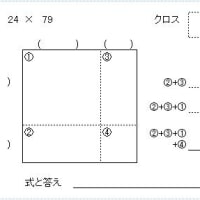
手順1:「内側の数同士をかけたもの」と「外側の数同士をかけたもの」を合計する。
手順2: これを10倍する。
手順3: これに、10の位の数字同士をかけたものを100倍し足す。
手順4: これに、1の位の数字同士をかけたものを足す。 → 答え
これで良いことになります。
つまり 78×63 を見ながら。。。
手順1: (内側)8×6+(外側)7×3 = 48+21= 69
手順2: これを10倍 → 690
手順3: これに、7×6×100を足す。
690
+4200 ← 桁を合わせて、数を下において足していくというイメージを持って下さい。
4890
手順4: これに、8×3 を足す。
4890
+ 24
4914
もっと単純化しましょう
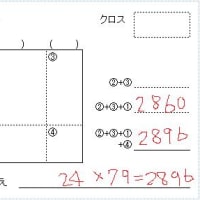
内側の数同士の積と外側の数同士の積を足して10倍、
これに、左側の数同士をかけた数の100倍を足し、
さらに、右側の数同士をかけた数を足す。
これで良いわけです。2桁掛け算の暗算法が3行で説明できました。
これでもし暗算が出来ない場合はどうしましょう。
それは、訓練をするしかないでしょう。
手順としては計算の心理的負担が発生しないよう、極限まで抑えた形となっています。
これ以上は簡素化出来ないでしょう。よってあとは訓練ですね。
最後に、さらにもうひと押し、計算の工夫を加えましょう。
それは、言わずもがなですが、上記の手順1で、内側同士の積と外側同士の積を合計するときに、
掛け算の分配法則等が使えるかもしれない、ということです。
つまり、例えば 88×43 などという計算だったら
8×4+8×3 = 8×(4+3)= 8×7 = 56 ですね。
32+24より「一瞬」速いかもしれません。
慣れてくると最も早い計算方法を自然に選べるようになります。
また、ちょっと裏技的ですが
、
76×39 だったらですね、
内側の積の 6×3 を 2×9 と読み替えてしまうんです。同じ18ですからね。
それで、
6×3+7×9=2×9+7×9=(2+7)×9=9×9=81
という工夫もできます。
これも、慣れると不思議なもので、すぐに 9×9 が浮かぶようになります。
そうなったら、実際に18+63=81 をするより、やや速いかな、という感じです。
まぁ、いろんな工夫をすることが楽しいわけです。
以上の方法に基づき、各自練習してみてください。きっと2桁の数の暗算が出来るようになると思います。
自分が良くやるのは車のナンバープレートをみて、左の数字と右の数字を掛け算することですね。
そんな感じで頭の体操をやっています。
また、上記の理論の延長上に「ねこ掛け算」があります 。「ねこ掛け算」では3桁の掛け算の暗算が出来るようになります。
。「ねこ掛け算」では3桁の掛け算の暗算が出来るようになります。
私も「自分がそんなことが出来るようになるなんて一生あり得ない」と考えておりましたが、
3桁同士の数の暗算が出来るようになりました。まぁ、時間は少々かかりますが、一応正解は出ます。
息子もですねぇ。。数が小さければ混乱せずに3桁掛け算が出来るように一時期はなりました。(今はだめですけれどもね。)
そこで次回は補足的になりますが、小学生にこの二桁暗算法を教える際の注意点ならびに方法論を実際の経験に基づいて述べたいと思います。


人気ブログランキングへ
まぁ、本当の究極の暗算法は丸暗記することかもしれませんが、それは置いておきまして。。
何故、そこまで言えるのかと申しますと、テーマが単純で手を入れる要素も少ないので、自分よりもっと頭のいい人が考えたとしても
これ以上先はもう無いだろう、と考えるからです。
この項は前半は理論であり、後半は具体的方法です。面倒くさい人は後半のみお読み下さい。
また、内容的には前回の記事の続きでもあるので、前回の記事も併せて読まれることをお勧めします。
まあ、私などが申すべくもなく、ネット等で検索するれば色々なものが出てきます。
その中には、ほとんど自分の考えたものと同じものも多々ありました。というか、考えている人は程んど同じ結論に達するのでしょう。
その同じ結論というのは、掛け算を4つの四角形の面積でかんがえるというやり方です。
たとえば 78×63 という計算なら以下のような四角形を考える。

これは計算のイメージとしては基本のものであり、理解しやすいと思います。
かつ子供に教えてもその後の数学的な思考展開の基礎となるものであり、意義のあることと考えます。
それでこの4つの四角形を足し上げて掛け算の答えを出すというものです。
つまり 4200+480+210+24
で、いくつになるかな 4914 ですな。
この四角形ををイメージしながら足し上げれば何とか暗算は出来るわけで、前回の4つの数の足し算をするという
内容と軌を一にします。
ただし、自分は時々単純計算であっても、「あれっ?」となってしまうタイプなので、それでもきつい場合がある。
もうちょっと工夫できないか。

工夫もなにも足し算する順番を考えるだけなのですが、色々と試行錯誤した結果、
四角形のうち右上と左下、この斜めのラインの合計を一番先に出すのが良いと考えました。
すなわち上記の例では 480+210 = 690 この計算を先ずやってしまう。
ここで 480 と 210 は 10の倍数になっていることに注意します。
その次に、左上、すなわち4200、100の倍数の数を足す。4890になる。
そして最後に右下の数、24という単純な九九の数を足す。 答えは 4914。
何故この順番なのか?

それは一つには各項を足し上げていくときに、
「先ずは、数字の桁の重なりが多いもの同士を最初に足してしまおう」 という考え方なんです。
つまり、480と210は10の倍数同士。これを先ずまとめてしまえ、ということです。
この場合は繰り上がりこそおきないものの、足し算するけたは100の位と10の位、
2つの桁でばっちりぶつかりあう。だからここでまず 690 という数をつくり10の倍数の合計を固めてしまう。
そこであとから4200を足し、24を足しという風にすれば、以降は足し算する桁が1桁しか重ならない。
(ただし、10の倍数の合計が1000を超えた場合は2桁重なることもある。)
この順番を変えると、どうなるか。

例えば 4200+480 = 4680 と先にやり、4680と210を次に足そうとすると
この2桁がぶつかりあうという最もこの足し算で過酷な部分で、最初に10の倍数同士を足した場合よりも大きな数を扱うことになる。
もう一つ、480+210を先ず行うというのは、これはゼロを除いて考えると両方とも九九の答えであり、
よく見なれた数字であるということであるからです。
ある意味既知の数であり、ある種計算にも慣れているその分心理的にも抵抗が少なく、速く計算出来る。
だからこそ、2桁の数がぶつかりあう足し算をここで行うのです。
これは実際、訓練を重ねていくと、きわめて限られた数字を扱っているのだと気付きます。
つまりは「九九の答え同士の足し算」なわけで、パターンとして限られてくるのです。
よって、だんだん慣れてくるということです。
要は間違っても 470+760 なんていう足し算はでてこないということですね。
もう一度まとめてみます

最初に10の倍数同士を足した場合
手順1: 480+210 = 690 → 二桁がぶつかりあう足し算だが、見なれた数字なので心理的抵抗小
手順2: 690+4200=4890 → 見なれぬ数字(690)を含むが、足し算する桁は1桁のみで心理的抵抗小
手順3: 4890+24 =4914 → 見なれぬ数字(4890)を含むが、足し算する桁は1桁のみで心理的抵抗小
順番を変えた場合
手順1: 4200+480=4680 → 見なれた数字なので心理的抵抗小
手順2: 4680+210=4890 → 見なれぬ数字(4680)を含み、足し算する桁も2桁であり、心理的抵抗大
手順3: 4890+24 =4914 → 見なれぬ数字(4890)を含むが、足し算する桁は1桁のみで心理的抵抗小
さらに、この順番が良いと考えるもう一つの理由があります。

それは、最初に作る10の倍数の項の合計が、たまたま100の倍数になることがあるということです。
これが100の倍数になった場合は、以降、下二桁の計算はあってないようなものです。
つまりこれがインド式計算のパターンに当たる場合の83×87などでは、4つの四角形の左下・右上の合計が800となる。
だからその後の足し算が楽になる、ということは前回述べました。
しかし、ここで注目したいのは、10の倍数の項の合計が100の倍数になるというパターンは、
インド式計算のパターンに当てはまる計算式だけではなく、他にも数多くあるということなんです。
例えば、64×77 = 4200+280+420+28
これは 最初に 280と420を足してしまえばあとは楽ですね。 4200+700+28 = 4928
あるいは 92×86 などもそうでしょうか。
7200+540+160+12 = 7200+700+12 = 7912 となりますね。
これは二桁同士の掛け算の計算パターンの3321通りのうち、401通りがそうなります。ちょっとした数です。
※3321通りというのは最初の記事でもふれましたが、二桁同士の掛け算のうち、1の位がゼロのものを除き、
さらにかけられる数とかける数を入れ替えたものを相殺したネットの計算式のパターンです。
よって、4つの四角形の各項のうち、まず、左下・右下の10の倍数の項を足すのが良いというのは御理解いただけたと思います。
そのあと、100の倍数の項、単純九九の項という順で足す、というのが私の提案する順序です。
この点については、残念ながら理屈はありません。
ただ、実際多くの計算にあたった結果、感覚的にこれが良いという結論に達しています。
以上が理論ですが、最後に具体的な方法論に入りたいと思います。
 究極の2桁掛け算暗算法
究極の2桁掛け算暗算法 :
:計算方法を具体化する際に、以上説明してきた「10の倍数の数の合計を出す」方法に関して
一つ変更を加えます。それは、「先ず九九の答え同士を足し、後から10倍する」ということです。
(同じことですよね)
それを踏まえて、例えば、78×63 という計算なら、
手順1:「内側の数同士をかけたもの」と「外側の数同士をかけたもの」を合計する。
手順2: これを10倍する。
手順3: これに、10の位の数字同士をかけたものを100倍し足す。
手順4: これに、1の位の数字同士をかけたものを足す。 → 答え
これで良いことになります。
つまり 78×63 を見ながら。。。
手順1: (内側)8×6+(外側)7×3 = 48+21= 69
手順2: これを10倍 → 690
手順3: これに、7×6×100を足す。
690
+4200 ← 桁を合わせて、数を下において足していくというイメージを持って下さい。
4890
手順4: これに、8×3 を足す。
4890
+ 24
4914
もっと単純化しましょう
内側の数同士の積と外側の数同士の積を足して10倍、
これに、左側の数同士をかけた数の100倍を足し、
さらに、右側の数同士をかけた数を足す。
これで良いわけです。2桁掛け算の暗算法が3行で説明できました。
これでもし暗算が出来ない場合はどうしましょう。
それは、訓練をするしかないでしょう。
手順としては計算の心理的負担が発生しないよう、極限まで抑えた形となっています。
これ以上は簡素化出来ないでしょう。よってあとは訓練ですね。
最後に、さらにもうひと押し、計算の工夫を加えましょう。

それは、言わずもがなですが、上記の手順1で、内側同士の積と外側同士の積を合計するときに、
掛け算の分配法則等が使えるかもしれない、ということです。
つまり、例えば 88×43 などという計算だったら
8×4+8×3 = 8×(4+3)= 8×7 = 56 ですね。
32+24より「一瞬」速いかもしれません。
慣れてくると最も早い計算方法を自然に選べるようになります。
また、ちょっと裏技的ですが
、
76×39 だったらですね、
内側の積の 6×3 を 2×9 と読み替えてしまうんです。同じ18ですからね。
それで、
6×3+7×9=2×9+7×9=(2+7)×9=9×9=81
という工夫もできます。
これも、慣れると不思議なもので、すぐに 9×9 が浮かぶようになります。
そうなったら、実際に18+63=81 をするより、やや速いかな、という感じです。
まぁ、いろんな工夫をすることが楽しいわけです。
以上の方法に基づき、各自練習してみてください。きっと2桁の数の暗算が出来るようになると思います。
自分が良くやるのは車のナンバープレートをみて、左の数字と右の数字を掛け算することですね。
そんな感じで頭の体操をやっています。
また、上記の理論の延長上に「ねこ掛け算」があります
 。「ねこ掛け算」では3桁の掛け算の暗算が出来るようになります。
。「ねこ掛け算」では3桁の掛け算の暗算が出来るようになります。私も「自分がそんなことが出来るようになるなんて一生あり得ない」と考えておりましたが、
3桁同士の数の暗算が出来るようになりました。まぁ、時間は少々かかりますが、一応正解は出ます。
息子もですねぇ。。数が小さければ混乱せずに3桁掛け算が出来るように一時期はなりました。(今はだめですけれどもね。)
そこで次回は補足的になりますが、小学生にこの二桁暗算法を教える際の注意点ならびに方法論を実際の経験に基づいて述べたいと思います。

人気ブログランキングへ