自分の息子が小学校三年生の当時、私は彼に2ケタ同士の掛け算の計算を教え、自らもいろいろと実践してみました。
まだ、2桁×1桁もどうなのよ、という感じでしたが、2桁×2桁が出来れば、それも自然と出来るだろうという強硬策を採りました。
前回提示した暗算法は、そのように子供に教えつつ、自分でも答え合わせで暗算をしつつ、という過程で形が練られていったと言えます。
よって計算法は、最初から出来上がったものがあったわけではありませんでした。
むしろ最初はインド式などを勇んで教えていました。
しかし早くのうちに、これらの計算術は今の子供に使わせるには少し不十分だなぁ、というか、無理だなぁと感じました。
理由は今まで何回か述べましたが、だいたい以下の通りです。
◎パターンによる規則的な計算法であったが、そのパターンがすぐには見抜けない。
◎この計算法によってカバーできる計算パターンが全体の中で極めて少ない。
◎パターンに当てはまったとしてもあまりにも簡単に計算できてしまうので計算練習の対象にならない。
◎何でその答えが正しくなるのか判らない。
など、ですね。
そこで何か良い方法がないかと模索し始めたのですが、すぐに4つの四角形を使った考え方は有効そうだと気がつきました。
これをベースに考え始めたのですが。。。息子は小学校三年生ですから、学校でまだ面積の考え方を習っていない(!)。

ノウハウだけを教えて叩き込むというのはやりたくなかったんですね。
ですので、「掛け算は四角形で表すことが出来るのだ」ということを先ず理解させることから始めました。
いくらうまい方法を思いついても、その計算過程がどうして正しい答えに結びつくか、これを一旦理解させた上で前に進めないと
意味がないと考えたわけです。






そこで、「力技」と言っては何ですが、マスの中に四角形の数を数えるための数字を書き込んだ方眼を用意しました。
実際に使用したものとは異なりますが、以下の感じです。
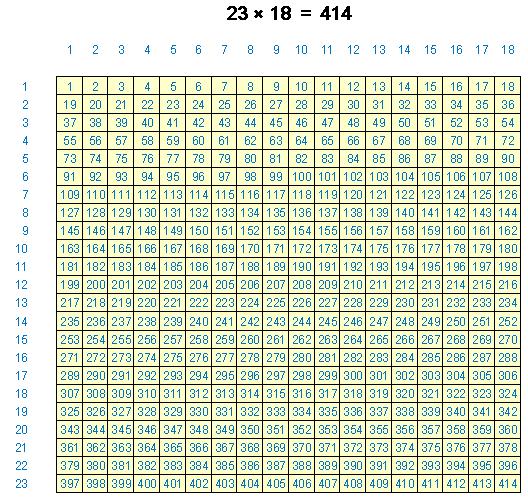
「23×18」を教えるためのものですが、23 と18 を各辺とする四角の方眼のマスの中に数字が書き込んであります。
まず、これを見せて、否が応でも掛け算は四角形で表すことができるのだ、ということを叩き込みます。
ビジュアルに確認させた後、計算機等をつかって実際に23×18をやってみて、「あっているでしょ」ということなります。
次に、この四角形を4つに分けてみよう、ということで次の図を見せます。
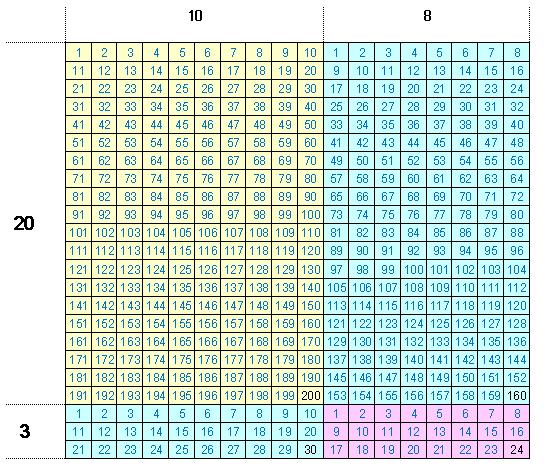
「10の位の数と1の位の数で分けて四角を4つにしました。」
「その一つ一つの四角の数の合計は全体と変わらないよね」ということを確認します。
その上で、次の図を見せます。
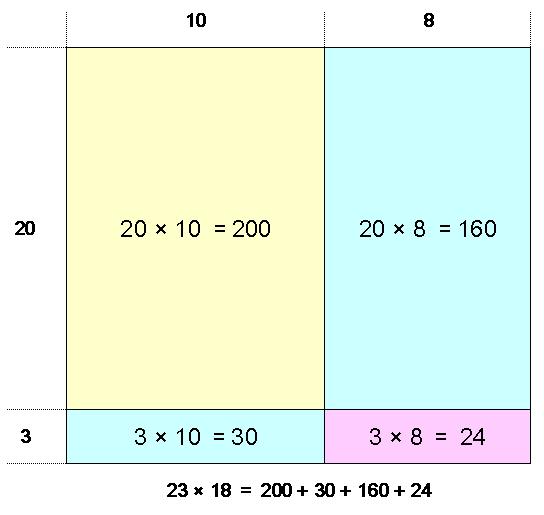
あれあれ、何やら簡単な掛け算におきかわったねぇ、と言いつつ、
「4つの掛け算の合計」が最初の 23×18 の答えと変わらないことを理解させます。
「そう、2ケタの数の掛け算は4つの四角を使って10の位と1の位で分けて考えることが出来るんだね」
「そして、答えは、その分けた掛け算の答えを足せばいいんだね」
以上を先ず、理解させる、というか、「そうなのか」という気持ちにさせます。






次に、前回の記事で説明しました計算法を習得させるためのドリルをやらせるわけですが、
これはしばらく、同じことを何週間かやらせるわけです。
そこで、毎回のドリルを始める前には、先ほどの 23×18 の3枚の図をおさらいします。
そうやって段々、身についてきます。
子供にやらせたドリルは実際どんなものか。こんな感じです。
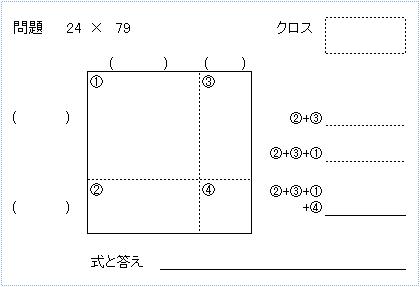
A4の全体図

このドリルはエクセルでシートを作りました。 >> 名付けて「クロス掛け算ワークシート」
問題は乱数で適当に出てくるようにしました。あと、同じ数があまり出てこないような工夫もちょっと入れました。
ちなみに2ケタの数の乱数を出すためには、以下の数式で出てきます。
エクセルでこのシートを作ってみたい方は、セルにそのままコピーして見て下さい。
(1の位にゼロがでてこないようになっています)
=10*(MOD(INT(100*RAND()),9)+1)+MOD(INT(100*RAND()),9)+1
それで、これをやらせた場合、実際どんな感じになるかというと。。。

こうなります。
順番としては、先ず、4つの四角形の数を埋めることが最初ですね。ここで掛け算のイメージを作ります。
次に、右上にある、「クロス」という四角の中に数を入れさせます。
※で、「クロス」ってなに?
ここで、一旦、前回説明しました計算法をおさらいします。
2ケタかけざん暗算法
手順1: 式の「内側の数同士をかけたもの」と「外側の数同士を掛けたもの」を合計する。
手順2: これを10倍する。
手順3: これに、10の位の数字同士をかけたものを100倍し足す。
手順4: これに、1の位の数字同士をかけたものを足す。 → 答え
ここで、手順1の ≪「内側の数同士をかけたもの」と「外側の数同士をかけたもの」の合計≫ を 「クロス」 と命名しました。
「クロス」という言葉は数学用語では別途定義があるようでしたので、多少使用を戸惑ったのですが、要は子供向けですので、
気にせず、とりあえずそういう名前を付けました。ついでに、この計算法を「クロス掛け算」と名付けました。
「四角を埋めたら、次はクロスを出してみて。。」とか、「クロスが間違っているんじゃないか?」とか言えるので、
名前をつけておいた方が何かと便利なわけです。
そうやって、最初は意味も判らず「クロス」なるものを計算して出すわけですが、もちろん、
この「クロス」は10倍すると(あるいは子供的には「お尻にゼロを付けると」)、四角の左下と右上の合計に等しくなるわけです。
そのことは最初はあえて明確にしなかったのですが、そのうち自然と気がつくわけですね。
意味が判らないことをやらせるのもどうかとは思いましたが、この点だけは自分で気がついて欲しいと考えました。
気がついたところを見計らって、「こことここの合計は、最初のクロスを10倍したものと同じだね、」と確認するわけです。
面白いことに、息子は「クロス」を計算する際に、自然と計算式の上と下に内側同士、外側同士を結ぶ線を引きながら、
そこにそれぞれの掛け算の答えを書くようになりました。それから横っちょの四角に、上下の数の合計を書き込むわけです。
(上の図にある通りです)

そうやって「クロス」を出してから、次にその下にある計算(各項の足し上げ)を順番にしてゆきます。
これが、暗算法の手順そのものになっています。先ず、10の倍数の合計(四角の左下と右上)を出し、
100の倍数、次に単純九九の部分を足す。そうやって掛け算の答えを出す。
そういう練習をするシートになっています。
よって、このワークシートを使って計算練習を重ねていくと、頭の中に暗算するための思考回路が
「数学的に意味のあるイメージ」とともに形成されてゆき、自然自然と暗算が出来るようになる、
という理屈なんですね。
そして最後には「式と答え」をキチンと書かせる。
これは2ケタの掛け算はこうやって解くことが出来るという意識付け、関連付けを明確にするためです。
息子の場合、ワークシートを毎日ではないがやらせてみて約6週間くらいで暗算が可能になったと記憶しています。
しかし実際はもっと早く出来るようになっていたのかも知れません。
というのも、6週間位たってから試しに暗算が出来るかどうかやってみたら、「出来た」ということだったんです。
ということで結果はもっと早く出るかもしれませんが、これは早く出来るようになれば良い、というものではないし、
要はしっかりとした計算練習を行って計算能力を地道に高めることが大事なのであって、
たとえ結果として暗算がマスターできなかったとしても、ワークシートをこつこつこなしたこと自体、
それはそれで頑張ったな、と言えるかと思います。




しかし、例えば、もう少し積極的に訓練的手法を取り入れるならば、以下の方法も考えられるでしょう。
ワークシートを使いつつも、下記のステップを踏んで徐々にレベルアップする。
1. 四角形のマスは空欄のまま、クロス、右側の計算式だけを埋める。
2. 四角形のマス、クロスと最初の計算式を飛ばし、いきなり2番目の式から計算を始める
↓具体的には。。。
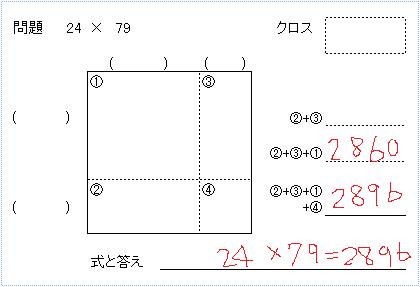
3. ワークシートを見ながら、いきなり4つの四角形の合計を出してみる(つまり掛け算の暗算をしてみる)
この手法を取り入れるときは、問題としては乱数から出すのではなく、先ずは数の少ない数字を選んでやってみると
良いでしょう。
そういえば、息子の場合もこれに似た形、何回かやりました。今思い出しました。
判らなくなったら、四角を埋めてから考えてごらん、というような形で、
徐々にハードルを上げていった様な記憶が。。。
まぁ、意外に出来てしまうものですよ。。。




以上が、前回ご案内した暗算法を小学生に教える際の方法論です。
足し算を頑張ることの出来るお子様ならば、誰にでも身に付くのではないかと考えます。
またこれは、学校教育における筆算の学習との整合性、並立性(違ったアプローチの計算法を教え込んで混乱が起きないかどうか)という点、
今後の数学的思考における発展性という点、これらについても自分になりに問題ないかどうか悩みつつたどり着いたものです。
その意味で、取り組んでみて無駄はない内容ではないかと考えております。



小学校教育 ブログランキングへ
まだ、2桁×1桁もどうなのよ、という感じでしたが、2桁×2桁が出来れば、それも自然と出来るだろうという強硬策を採りました。
前回提示した暗算法は、そのように子供に教えつつ、自分でも答え合わせで暗算をしつつ、という過程で形が練られていったと言えます。
よって計算法は、最初から出来上がったものがあったわけではありませんでした。
むしろ最初はインド式などを勇んで教えていました。

しかし早くのうちに、これらの計算術は今の子供に使わせるには少し不十分だなぁ、というか、無理だなぁと感じました。
理由は今まで何回か述べましたが、だいたい以下の通りです。
◎パターンによる規則的な計算法であったが、そのパターンがすぐには見抜けない。
◎この計算法によってカバーできる計算パターンが全体の中で極めて少ない。

◎パターンに当てはまったとしてもあまりにも簡単に計算できてしまうので計算練習の対象にならない。
◎何でその答えが正しくなるのか判らない。

など、ですね。
そこで何か良い方法がないかと模索し始めたのですが、すぐに4つの四角形を使った考え方は有効そうだと気がつきました。
これをベースに考え始めたのですが。。。息子は小学校三年生ですから、学校でまだ面積の考え方を習っていない(!)。

ノウハウだけを教えて叩き込むというのはやりたくなかったんですね。
ですので、「掛け算は四角形で表すことが出来るのだ」ということを先ず理解させることから始めました。
いくらうまい方法を思いついても、その計算過程がどうして正しい答えに結びつくか、これを一旦理解させた上で前に進めないと
意味がないと考えたわけです。






そこで、「力技」と言っては何ですが、マスの中に四角形の数を数えるための数字を書き込んだ方眼を用意しました。
実際に使用したものとは異なりますが、以下の感じです。

「23×18」を教えるためのものですが、23 と18 を各辺とする四角の方眼のマスの中に数字が書き込んであります。
まず、これを見せて、否が応でも掛け算は四角形で表すことができるのだ、ということを叩き込みます。
ビジュアルに確認させた後、計算機等をつかって実際に23×18をやってみて、「あっているでしょ」ということなります。
次に、この四角形を4つに分けてみよう、ということで次の図を見せます。

「10の位の数と1の位の数で分けて四角を4つにしました。」
「その一つ一つの四角の数の合計は全体と変わらないよね」ということを確認します。
その上で、次の図を見せます。

あれあれ、何やら簡単な掛け算におきかわったねぇ、と言いつつ、
「4つの掛け算の合計」が最初の 23×18 の答えと変わらないことを理解させます。
「そう、2ケタの数の掛け算は4つの四角を使って10の位と1の位で分けて考えることが出来るんだね」
「そして、答えは、その分けた掛け算の答えを足せばいいんだね」
以上を先ず、理解させる、というか、「そうなのか」という気持ちにさせます。






次に、前回の記事で説明しました計算法を習得させるためのドリルをやらせるわけですが、
これはしばらく、同じことを何週間かやらせるわけです。
そこで、毎回のドリルを始める前には、先ほどの 23×18 の3枚の図をおさらいします。
そうやって段々、身についてきます。
子供にやらせたドリルは実際どんなものか。こんな感じです。

A4の全体図

このドリルはエクセルでシートを作りました。 >> 名付けて「クロス掛け算ワークシート」
問題は乱数で適当に出てくるようにしました。あと、同じ数があまり出てこないような工夫もちょっと入れました。
ちなみに2ケタの数の乱数を出すためには、以下の数式で出てきます。
エクセルでこのシートを作ってみたい方は、セルにそのままコピーして見て下さい。
(1の位にゼロがでてこないようになっています)
=10*(MOD(INT(100*RAND()),9)+1)+MOD(INT(100*RAND()),9)+1
それで、これをやらせた場合、実際どんな感じになるかというと。。。

こうなります。
順番としては、先ず、4つの四角形の数を埋めることが最初ですね。ここで掛け算のイメージを作ります。
次に、右上にある、「クロス」という四角の中に数を入れさせます。
※で、「クロス」ってなに?

ここで、一旦、前回説明しました計算法をおさらいします。
2ケタかけざん暗算法
手順1: 式の「内側の数同士をかけたもの」と「外側の数同士を掛けたもの」を合計する。
手順2: これを10倍する。
手順3: これに、10の位の数字同士をかけたものを100倍し足す。
手順4: これに、1の位の数字同士をかけたものを足す。 → 答え
ここで、手順1の ≪「内側の数同士をかけたもの」と「外側の数同士をかけたもの」の合計≫ を 「クロス」 と命名しました。
「クロス」という言葉は数学用語では別途定義があるようでしたので、多少使用を戸惑ったのですが、要は子供向けですので、
気にせず、とりあえずそういう名前を付けました。ついでに、この計算法を「クロス掛け算」と名付けました。
「四角を埋めたら、次はクロスを出してみて。。」とか、「クロスが間違っているんじゃないか?」とか言えるので、
名前をつけておいた方が何かと便利なわけです。
そうやって、最初は意味も判らず「クロス」なるものを計算して出すわけですが、もちろん、
この「クロス」は10倍すると(あるいは子供的には「お尻にゼロを付けると」)、四角の左下と右上の合計に等しくなるわけです。
そのことは最初はあえて明確にしなかったのですが、そのうち自然と気がつくわけですね。
意味が判らないことをやらせるのもどうかとは思いましたが、この点だけは自分で気がついて欲しいと考えました。
気がついたところを見計らって、「こことここの合計は、最初のクロスを10倍したものと同じだね、」と確認するわけです。
面白いことに、息子は「クロス」を計算する際に、自然と計算式の上と下に内側同士、外側同士を結ぶ線を引きながら、
そこにそれぞれの掛け算の答えを書くようになりました。それから横っちょの四角に、上下の数の合計を書き込むわけです。
(上の図にある通りです)

そうやって「クロス」を出してから、次にその下にある計算(各項の足し上げ)を順番にしてゆきます。
これが、暗算法の手順そのものになっています。先ず、10の倍数の合計(四角の左下と右上)を出し、
100の倍数、次に単純九九の部分を足す。そうやって掛け算の答えを出す。
そういう練習をするシートになっています。
よって、このワークシートを使って計算練習を重ねていくと、頭の中に暗算するための思考回路が
「数学的に意味のあるイメージ」とともに形成されてゆき、自然自然と暗算が出来るようになる、
という理屈なんですね。
そして最後には「式と答え」をキチンと書かせる。
これは2ケタの掛け算はこうやって解くことが出来るという意識付け、関連付けを明確にするためです。
息子の場合、ワークシートを毎日ではないがやらせてみて約6週間くらいで暗算が可能になったと記憶しています。
しかし実際はもっと早く出来るようになっていたのかも知れません。
というのも、6週間位たってから試しに暗算が出来るかどうかやってみたら、「出来た」ということだったんです。
ということで結果はもっと早く出るかもしれませんが、これは早く出来るようになれば良い、というものではないし、
要はしっかりとした計算練習を行って計算能力を地道に高めることが大事なのであって、
たとえ結果として暗算がマスターできなかったとしても、ワークシートをこつこつこなしたこと自体、
それはそれで頑張ったな、と言えるかと思います。




しかし、例えば、もう少し積極的に訓練的手法を取り入れるならば、以下の方法も考えられるでしょう。
ワークシートを使いつつも、下記のステップを踏んで徐々にレベルアップする。
1. 四角形のマスは空欄のまま、クロス、右側の計算式だけを埋める。
2. 四角形のマス、クロスと最初の計算式を飛ばし、いきなり2番目の式から計算を始める
↓具体的には。。。

3. ワークシートを見ながら、いきなり4つの四角形の合計を出してみる(つまり掛け算の暗算をしてみる)
この手法を取り入れるときは、問題としては乱数から出すのではなく、先ずは数の少ない数字を選んでやってみると
良いでしょう。
そういえば、息子の場合もこれに似た形、何回かやりました。今思い出しました。
判らなくなったら、四角を埋めてから考えてごらん、というような形で、
徐々にハードルを上げていった様な記憶が。。。

まぁ、意外に出来てしまうものですよ。。。




以上が、前回ご案内した暗算法を小学生に教える際の方法論です。
足し算を頑張ることの出来るお子様ならば、誰にでも身に付くのではないかと考えます。
またこれは、学校教育における筆算の学習との整合性、並立性(違ったアプローチの計算法を教え込んで混乱が起きないかどうか)という点、
今後の数学的思考における発展性という点、これらについても自分になりに問題ないかどうか悩みつつたどり着いたものです。
その意味で、取り組んでみて無駄はない内容ではないかと考えております。


小学校教育 ブログランキングへ









