心においても、ロボットは人間よりも人間らしくなりうる。
ただしこれは程度の問題で、今でも人間同士が心で対立し合うように、ロボットの心が人間より上回るとか、相容れるとかいうことではない。しばらくは人間もロボットの心については歯牙にもかけないだろう。
しかし、やがて人間に必要な物のすべてをロボットが提供できるようになると、ロボットの心についても無頓着ではいられなくなる。そうなると、認める認めないに関わらず、人間の心はロボットの心に多大な影響を受けることになる。
最も恐いのは、そのことに気づくことなく、ロボットの社会が構築されてしまうことだ。
そうなる前に人間はロボットの心を学ぶ必要がある。より良いロボット社会のためにも。
ロボットの時代。
人間の特権と思い込んでいたものが幻想に過ぎないと認めるのは、つらく悲しい出来事になるだろう。
人間の心は不完全で脆いものだから、ロボットに頼りきって生きるのは、ある意味自然なのかもしれない。
地球に人間だけが生きているわけではない。
生命がいないような惑星も太陽を廻っている。
銀河に恒星は無数に輝き、宇宙は無限の広がりをもつ。
では、人間が人間として生きるとは?











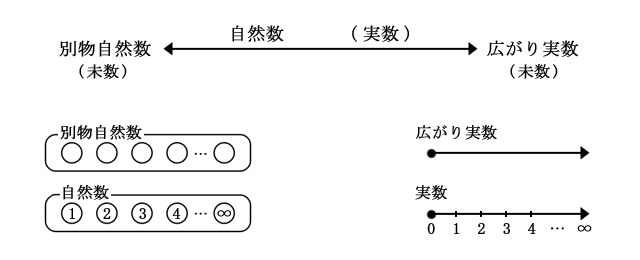
 で解いてみる。
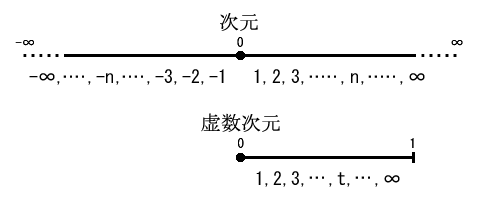
で解いてみる。
 はiとされるが、正確には1・iで、1次元を半次元にした時の異性体であった名残り。
はiとされるが、正確には1・iで、1次元を半次元にした時の異性体であった名残り。