クローズアウト対プライム戦における勝率の見積もり方 その2

勝率の見積もり方は

勝率 = 33　＋　（タイミングのピップ数）　－　（プライム脱出に必要な平均ピップ数）　＋　（オンザバーの枚数によるボーナス）　＋　50　＋（補正）

このように単純な足し引きで求められることまでを前回話しました。では具体的にどうやって求めるかを以下のポジションを例に説明します。

 

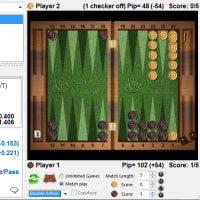
ポジション　A（再掲）

(1)タイミングのピップ数。クローズアウトに必要なチェッカーや5プラに捕まっているチェッカー以外のチェッカー（ポジションAでは6Pと17Pにあたる）が1Pまでに何ピップ余裕があるか、そのピップ数の総和を取ったものです。すなわち上の例では（6-1)　+　(17-1) = 21　となります。

 

(2)プライム脱出に必要な平均ピップ数。これは5プラに捕まっているチェッカーを逃しきるのに要するロール数をピップに換算した値のことです。　おおざっぱですが一回ロールして6が出る確率は約1/3で、一回のロールで進む平均ピップ数は約8ピップです。6を出して5プラを脱出するためには期待値的に3ロール必要で、これをピップ数に換算すると3×8=24　ピップとなります。　

 

(3)オンザバーの枚数によるボーナス。相手のチェッカーがバーに1枚あるときは0、2枚あるときは6となります。3枚あるときはやや不正確になりますが9ぐらいになります。ポジションAの例では1枚なので0となります。

 

(4)補正。ポジションAは補正が特に必要ない形です。どういう場合に必要かは次回述べます。

 

 

 では公式に当てはめますと

 勝率 = 33　＋　（タイミングのピップ数）　－　（プライム脱出に必要な平均ピップ数）　＋　（オンザバーの枚数によるボーナス）　＋　50　＋（補正）

代入して

33 + 21 - 24 + 0 + 50 + 0 = 80%　が得られます。したがってマネーゲームで黒がここでキューブを打てば白はパスします。

XG2によるロールアウトの結果とキューブアクションは以下のとおりです。ぴったりと一致しました。

 

Analyzed in Rollout
No double
Player Winning Chances: 80.08% (G:2.23% B:0.03%)
Opponent Winning Chances: 19.92% (G:1.14% B:0.03%)
Double/Take
Player Winning Chances: 80.19% (G:2.15% B:0.03%)
Opponent Winning Chances: 19.81% (G:1.14% B:0.03%)

Cubeless Equities: No Double=+0.613, Double=+1.228

Cubeful Equities:
No double: +0.842 (-0.158)
Double/Take: +1.119 (+0.119)
Double/Pass: +1.000

Best Cube action: Double / Pass

Rollout:
5184 Games rolled with Variance Reduction.
Dice Seed: 93543280
Moves: 2-ply, cube decisions: 3-ply Red

eXtreme Gammon Version: 2.03

 

 

ポジションC

 

次の例は相手のチェッカーが2枚あり、自分のチェッカーが2枚捕まっている場合です。

タイミングのピップ数は12。オンザバーの枚数によるボーナスは6です。

プライム脱出に必要な平均ピップ数については少し工夫が要ります。1枚捕まっている場合は24ピップなので単純に2倍して48ピップとなりそうなところですが、実は1枚目のチェッカーを逃すことでタイミングのピップ数が新たに増えることを考慮する必要があります。つまり1回6を振って1枚抜け出すと17ピップの余裕が新たに得られます。この影響を頭で計算することは困難なので、ロールアウトの結果とつじつまが合うように値を求めました。この値が48から10引いた38となります。　ピップのタイミングに10加えても解釈が異なるだけで同じ結果が得られます。

式に代入すると

33 + 12 - 38 + 6 + 50 =  63% が得られました。　XG2によるロールアウトの結果とほぼ一致します。

 

Analyzed in Rollout
No double
Player Winning Chances: 63.02% (G:21.91% B:0.51%)
Opponent Winning Chances: 36.98% (G:7.58% B:0.27%)
Double/Take
Player Winning Chances: 63.33% (G:21.42% B:0.49%)
Opponent Winning Chances: 36.67% (G:7.63% B:0.27%)

Cubeless Equities: No Double=+0.406, Double=+0.813

Cubeful Equities:
No double: +0.394 (-0.167)
Double/Take: +0.561
Double/Pass: +1.000 (+0.439)

Best Cube action: Double / Take

Rollout:
5184 Games rolled with Variance Reduction.
Dice Seed: 57982384
Moves: 2-ply, cube decisions: 3-ply Red

eXtreme Gammon Version: 2.03

 

 なんだか一致しすぎていてかえって胡散臭いのですが、だいたい±0.5%の範囲内に誤差が収まります。

ただしいくつか例外的に誤差が大きくなりポジションがあり、その場合補正が必要になります。その方法についてはまた次回ということで。　

 

つづく…