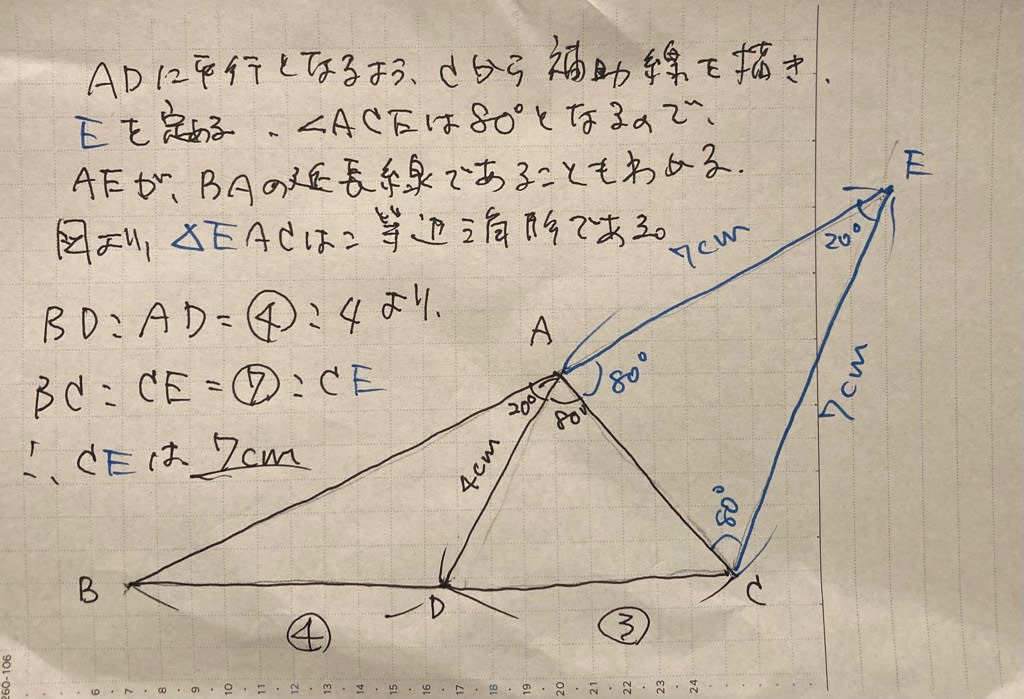
「 船が川の下流のA地点から48km上流のB地点まで行くのにいつもは6時間かかります。ある日、エンジンが途中で30分動かなくなったので、A地点からB地点まで行くのに6時間39分かかりました。ただし、船の静水での速さと川の流れの速さはそれぞれ一定とします。
(1)川の流れの速さは時速何kmですか、求め方と答えを書きなさい。
(2)いつもはA地点とB地点を往復するのに何時間何分かかりますか。 」2002
(1)川の流れの速さは時速何kmですか、求め方と答えを書きなさい。
(2)いつもはA地点とB地点を往復するのに何時間何分かかりますか。 」2002
(1)船がA地点からB地点までの48kmを上るのに6時間かかるということは、上りの速さは時速8km。
「エンジンが途中で30分動かなくなった」ということは、その間、川の流れの速さにより、下流へと流されていたと考えることができる。
そして、A地点からB地点まで行くのに6時間39分かかり、流されていただけの時間が30分あれば、実際に上った時間は6時間9分である。いつもは6時間で上るとすると、余分に9分かかったことになる。とすると、船は流されていた30分の距離を9分で上った。同じ距離を30分か9分かで移動した速さの比は逆比となり、つまり、川の流れの速さと上りの速さの比は、9:30(3:10)。
上りの速さは時速8kmなので、その3/10が川の流れの速さであり、時速2.4km(答え)
(2)船が、川を、
上る速さとは、(船の速さ)ー(川の流れの速さ)であり、
下る速さとは、(船の速さ)+(川の流れの速さ)である。
いつも、どこの中学入試算数問題でも。
上りの速さが時速8kmで、川の流れの速さが時速2.4kmであれば、船の速さは時速10.4km。とすると、下りの速さは、10.4 + 2.4となり、時速12.8km。
48(AB間の距離) ÷ 12.8(下りの速さ)
=480/128
=15/4(時間)
60倍すると、225分。つまり、下りにかかる時間は3時間45分。
上りに6時間かかるので、上りと下りを合わせた往復時間は9時間45分(答え)
コレは、とても良い問題。感心させられたわ。正答のみならず、採点者の納得のゆく説明も必要だ。
当然のことながら、まず、問題文を読めなくては解けない。たとえば、「エンジンが途中で30分動かなくなった 」といっても、船が止まっているわけではない。流されていること、そこに純然たる川の流れ(の速さ)が働いていることをその言外で理解しなくては解けない。
さっきの女子学院の素数を扱わせる論理問題も手厳しく難しかったでしょう。












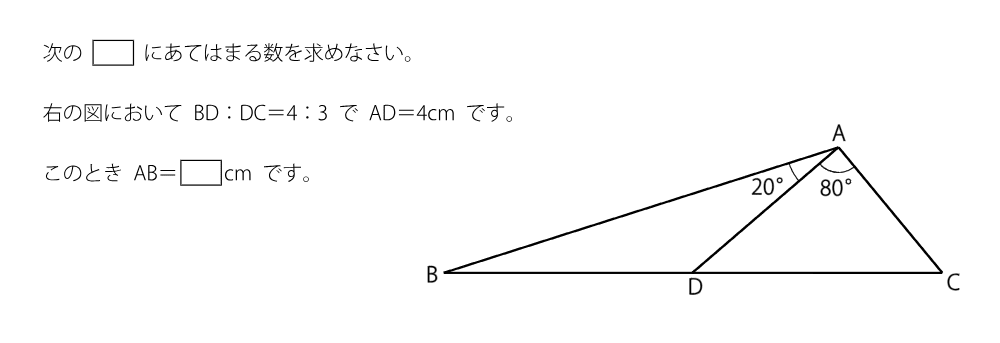 2014
2014