H24年二種の理論に面白い問題を発見した「Isht」の練習に最適である。

A1: V2=-I2R3、 V3=-I2(R3+R2)
∴V3/V2=(R3+R2)/R2=(2+4)/2=3
※直感的には2倍と思いたくなるのが、落とし穴である。
A2: I2は、「Isht」等価回路から
(V3-V1)=(V3-V2)となり、
-I1R1=-I2R2
∴I2=I1R1/R2=0.1×8/4=0.2(mA)
A3: V2=-I2R3=-0.2×2=-0.4(V)
A4: V3=--I2R2=-0.2×4=-0.8(V)
A5: V1/I1=-0.4/0.1=-4(KΩ)
※Q5で求めている性質は、通常の抵抗と異なり⊖4KΩの負性抵抗である。
・この問題に興味を持ったのは負性抵抗(⊖R)が現われることである。RCLの組み合わせで出来ているブリッジT型トラップも(⊖R/4)の負性抵抗が現われるが、オペアンプでの負性抵抗は初めての出会いである。
☟オペアンプ以外でも負性抵抗を利用している回路がある。アナログTVで用いられていたブリッジT型トラップは、コイルの巻き線抵抗を負性抵抗で打ち消すことで理想的な直列共振回路を構成していた。
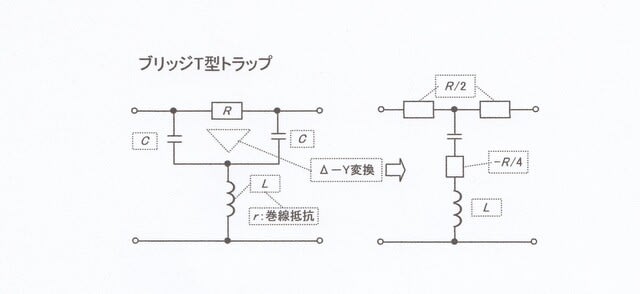
☝RCのデルタ回路部分をスターに変換する過程で負性抵抗が生じる。Δ-Y変換の練習にチャレンジする価値がある。
・強電では、負性抵抗との付き合いは少ないと考えられるが、無線屋は負性抵抗との付き合いが長く、真空管時代に学んだダイナトロン特性がある。
・負性抵抗があると、容易に発振回路が構成できる。半導体になってから有名なのは1972年にノーベル賞受賞のエサキダイオードであるが、現在は入手困難と考えられる。しかし、λダイオードが入手可能なので発振回路の実験ができる。
・負性抵抗を利用した発振回路で最も実験したのがUJT(Unijunction Transistor)である。UJTは、またの名をダブルベースダイオード(double base diode)とも言う。
・負性抵抗は、V-I特性で電圧が増加する過程で電流が減少する特性を負性抵抗領域といい、図のような特性をダイナトロン特性という。

☝発振動作は、コンデンサの充電が進みエミッタ-ベース間が順方向になると、エミッタからの注入で伝導度変調が起こりB1-B2が導通する。
・コンデンサの電荷はC⇒VR⇒R1⇒R2⇒Cと放電する。放電が終わると、UJTはOFFとなり、コンデンサの充電が開始し、スタート点に戻る。





























