算額（その1） 大円，中円，小円（解決編）

算額（その1）

算額--2022年
https://blog.goo.ne.jp/r-de-r/e/12c8f8f08dbedbd16d5b8f54e32a17a8

が解けた。自力でやったのではなく，SymPy を使って。それでも相当骨が折れた。

三重県三重郡三重郡菰野町 廣幡神社 文化9年(1812)
http://www.wasan.jp/mie/hirohata2.html

山形県鶴尾市大山 椙尾神社 文政元年(1818年8月)
http://www.wasan.jp/yamagata/sugio.html

一〇一 大宮市高鼻町 氷川神社 明治31年(1898)
埼玉県立図書館：埼玉県史料集 第二集『埼玉の算額』，昭和44年，誠美堂印刷所，埼玉県与野市.

岩手県一関市花泉町 大門神社・大門観世音菩薩 明治33年(1900)
http://www.wasan.jp/iwate/daimon5.html

答えは，「外側の円の半径を 1 とすると，大円，中円，小円の半径はそれぞれ (9 + √17)/32，(23 - √17)/64，(5 - √17)/4 である。」

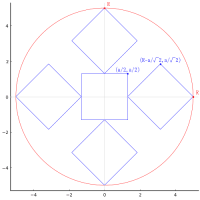
三種類の円を含む外側の円が，原点を中心とする半径 1 の円とする。

図と記号の対応を示す。

using SymPy

@syms x, y
@syms α::real, β::real, γ::real # 大円，中円，小円の半径
@syms φ::real         # 上の大円の中心の y 座標
@syms χ::real;        # 右上の中円の中心の x 座標

## 1.　それぞれの円の方程式

αeq = x^2 + (y - φ)^2 - α^2 # 大円の方程式

βeq = (x - χ)^2 + (y - β)^2 - β^2 # 中円の方程式

γeq = (x - γ)^2 + y^2 - γ^2 # 小円の方程式

## 2.　通過点による制約

eq1 = αeq(x => 0, y => 1) # (0, 1)

eq2 = αeq(x => 0, y => 1-2α) # (0, 1-2*α)

## 3.　重心間の距離による制約

eq5 = χ^2 + (1 - α - β)^2 - (α + β)^2 # α to β

eq6 = (χ - γ)^2 + β^2 - (γ + β)^2 # γ to β

eq7 = γ^2 + (1 - α)^2 - (α + γ)^2 # α to γ

## 4.　大円と中円の接点で成り立つこと

eq8 = sqrt(χ^2 + β^2) + β - 1

answer = solve([eq1, eq2, eq5, eq6, eq7, eq8], (φ, α, χ, β, γ))

    3-element Vector{NTuple{5, Sym}}:
     (0, 1, -1, 0, -1/2)
     (23/32 - sqrt(17)/32, sqrt(17)/32 + 9/32, sqrt(2)/sqrt(9 - sqrt(17)), 23/64 - sqrt(17)/64, 5/4 - sqrt(17)/4)
     (sqrt(17)/32 + 23/32, 9/32 - sqrt(17)/32, -sqrt(2)/sqrt(sqrt(17) + 9), sqrt(17)/64 + 23/64, sqrt(17)/4 + 5/4)

二組の解が得られるが，最初のものは明らかに不適である。

φ2, α2, χ2, β2, γ2 = [answer[2][i] for i in 1:5]

eq1, eq2 を検算してみる。

eq1(α　=> α2, φ => φ2).evalf() |> println

    0

eq2(α　=> α2, φ => φ2).evalf() |> println

    -0.e-124

eq5, eq6, eq7 を検算してみる。

eq5(χ => χ2, α => α2, β => β2).evalf() |> println
eq6(β => β2, γ => γ2, χ => χ2).evalf() |> println
eq7(γ => γ2, α => α2).evalf() |> println

    -0.e-125
    -0.e-125
    -0.e-125

eq8 を検算してみる。

eq8(χ => χ2, β => β2).evalf() |> println

    -0.e-125

## 5.　大円の半径

α2 |> println

    sqrt(17)/32 + 9/32

α2 |> println

    sqrt(17)/32 + 9/32

α2 |> N

    0.410097050800551892181919057999189907035849975792925638574957299159217323323052

## 6.　中円の半径

β2 |> println

    23/64 - sqrt(17)/64

β2 |> N

    0.2949514745997240539090404710004050464820750121035371807125213504203913383384761

## 7.　小円の半径

γ2 |> println

    5/4 - sqrt(17)/4

γ2 |> N

    0.2192235935955848625446475360064807437132001936565948914003416067262614134155944

## 8.　大円の中心の y 座標

φ2 |> println

    23/32 - sqrt(17)/32

φ2 |> N

    0.5899029491994481078180809420008100929641500242070743614250427008407826766769523

## 9.　中円の中心の x 座標

χ2 |> println

    sqrt(2)/sqrt(9 - sqrt(17))

χ2 |> N

    0.6403882032022075687276762319967596281433999031717025542998291966368692932921995

二重根号を外して，簡約化する。

χ22 = sympy.sqrtdenest(χ2) |> simplify |> factor
χ22 |> println

    (1 + sqrt(17))/8

χ22 |> N

    0.6403882032022075687276762319967596281433999031717025542998291966368692932921995

## 10.　確認のため図を描いてみる

using Plots

function circle2(ox, oy, r, color)
    theta = 0:0.01:2pi
    x = r.*cos.(theta)
    y = r.*sin.(theta)
    plot!(ox .+ x, oy .+ y, color=color)
end;

gr(size=(500, 500), aspectratio=1, label="")
plot()
circle2(0, φ2, α2, :red) # 大円
circle2(0, -φ2, α2, :red)

circle2(χ2, β2, β2, :green) # 中円
circle2(χ2, -β2, β2, :green)
circle2(-χ2, β2, β2, :green)
circle2(-χ2, -β2, β2, :green)

circle2(γ2, 0.0, γ2, :black) # 小円
circle2(-γ2, 0.0, γ2, :black)

circle2(0, 0, 1, :blue); # 外円

savefig("fig1.png");

冒頭に示した，図と記号の対応を示すもの

3 つの円と，7 つのパラメータ

(cax, cay) = (0, convert(Float64, φ2))
(cbx, cby) = (convert(Float64, χ2), convert(Float64, β2))
(ccx, ccy) = (convert(Float64, γ2), 0)
(ra, rb, rc) = (convert(Float64, α2), convert(Float64, β2), convert(Float64, γ2))
annotate!(cax, cay, text("(0, φ)", 10, :center, :top))
annotate!(cbx,cby, text("(χ, β)", 10, :center, :top))
annotate!(ccx, ccy, text("γ, 0)", 10, :center, :top));

sx = [0.0, convert(Float64, χ2), convert(Float64, γ2)]
sy = [convert(Float64, φ2), convert(Float64, β2), 0.0]
scatter!(sx,sy);

ex = [cax, cbx, ccx] .+ [ra, rb, rc]
ey = [convert(Float64, φ2), convert(Float64, β2), 0.0]
scatter!(ex, ey);

for i in 1:3
    annotate!((sx[i] + ex[i])/2 , (sy[i] + ey[i])/2, text(["α", "β", "γ"][i], 10, :bottom))
    plot!([sx[i], ex[i]], [sy[i], ey[i]])
end
plot!()

circle2(-γ2, 0.0, γ2, :black)

circle2(0, 0, 1, :blue) # 外円

savefig("fig0.png");