このクソ暑い中で、3話続けての数学ネタですが、どうかお付き合いくださいませ。 前回「その4」では、ガウスの正17角形の作図可能性を少し突っ込んで説明しましたが、今回は、そのガウスですら解けなかった正7角計の作図について書きたいと思います。ケーキを7等分するには 数学を愛する会(@mathlava)さんが開催した、”ケーキを7等分する”選手権。 最優秀賞に輝いたのは、「定規 . . . 本文を読む
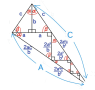
数学と人種の壁 アメリカ数学会で2人の10代の少女がピタゴラスの定理について、新しい証明方法をプレゼンした事が話題になっている。 応用数学の専門家であるキース・マクナルティ氏は”性別・民族・社会人口学的背景に関係なく、誰でも研究分野での卓越性は達成可能である事を示す素晴らしい出来事”と評してる他、その証明方法自体が波紋を呼んでいる。 数学会にはあまり例がない南部出身のアフリ . . . 本文を読む
前回「その3」では、cos(2π/17)を求め、正17角形の頂点を示す式であるx¹⁷−1=0の(自明なx=1を除けば)16個の解を2次方程式を有限回(3回)解く事で導き出しました。 そして、この事はcos(2π/17)が”四則とルートのみで表せる”事と同義である事は何度も触れました。 前回のおさらいですが、ガウスは((17等分ー1)/2= . . . 本文を読む
前回の記事に寄せられたコメントに、素数は”他人の介入を許さない孤高な数”とあった.つまり、素数と同じ孤高の数学者が憑かれるのも当然ではある。そんな私もどちらかと言えば、孤独の人間なので素数に惹かれるのだろう。 一方で、そんな魅惑的な素数ですが、13や17の様に悪魔的な側面を持つ。呪われた数とまでは言わないが、長年忌み嫌われ続けた負の歴史を持つ。 しかし、近年の盛んな素数の . . . 本文を読む
あるフォロワーの記事に”素数ゼミ”の事が書かれてあった。最初は素数ゼミナールの話かと思ったが、何とセミと素数のお話である。 素数に関しては、リーマン・ブログで数多くテーマにしてきたつもりだが、素数ゼミの事をすっかり忘れていた。つまり、セミだけでなく数学が生き延びてきた上で大切な役割を果たしてきたのが素数である。 古代から人々を魅了してきたこの素数だが、今でも数多くの数学者 . . . 本文を読む
ガウスはどうやって正17角形を描いたのか? (私もウッカリでしたが)実は、ガウスは実際の作図法を思いついたのではなく、数学的に作図が可能である事に気がついた。 つまり、正17角形の頂点を示す式であるx¹⁷−1=0の17個(自明なx=1を除けば16個)の解が2次方程式を有限回(3回)解くだけで導ける事でした。 そして、この事はcos(2π/17)が四則とルートのみで表せ . . . 本文を読む
TVドラマ「やまとなでしこ」 (2000年、フジTV系)でウエディングケーキを68人で分けるというシーンがあったそうだ。 が、私は全く覚えていない。というのも女優として全盛期を迎えていた松嶋菜々子さんがあまりにも美しすぎて、数学なんてどうでもよかったのだろう。 流石の数学の美しさも、若い女の可憐さには遠く及ばなかったのである。 事実(ウィキによれば)、全11話で平均視聴率26.4%、最高視聴率は . . . 本文を読む
「人生の答えは1つじゃない」に寄せられたコメントを久しぶりに読んでたら、良いこと書かれてあるなと、思わず感心する。 つまり、数学者一人一人に答えがあり、最終的には1つに美しく見事に凝縮していく。 ウイルスを含めたいかなる命も、変異と淘汰を繰り返し、進化を遂げる事で生き延びてきた。これは人も数学も同じである。 半生命体であろうが、生身の人間であろうが、近くで戯れ付く猫であろうが、行動それぞれに答え . . . 本文を読む
人間というのは、堅苦しい事や難しい事ばかりじゃ当然だが、頭がおかしくなる訳で、個人的な事や日常的なる事を徒然なるままに書き記すのも気分転換にはなるが、そればかりじゃバカ?になる。 基本的にBlogってのは、”言葉の肥溜め”であり”感情の排泄”に過ぎない。SNSだって同じだろう。つまり、世界中に網羅される”情報の吐き溜め”に他 . . . 本文を読む