
原子核のまわりの電子雲の様子
虚数は私たちの世界観を変えてしまった。
高校の数学で虚数というものを学習する。この世に存在しない数として紹介されるのだ。どうして存在しないものを学ぶ必要があるのだろうと不思議に思った人もいるに違いない。
虚数は i という文字であらわし、次のような式で紹介される。
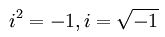
i を2回掛けると -1 になるというのが虚数の定義だ。i には「大きさ」というものを考えないので i < 2i とかいう不等式は意味をなしていない。狐につままれたような感じがするのは大きさを考えられないのに「数」と呼んでいるからだろう。
参考: 虚数や複素数に大小関係がないことは、次のページで証明しておいた。
虚数や複素数に大小がないのはなぜ?
https://blog.goo.ne.jp/ktonegaw/e/398b0d7e84eb491dea9c38a15e994256
けれどもこの虚数はこれから説明するようにこの世界、つまり物質や時間、空間のことを物理法則で解明するためには必要不可欠なモノであることがわかったのだ。「存在しない数」を使ってこの世界が存在していることが裏づけられるなんて変な理屈だと思われるかもしれない。
なぜなら物質や時間、空間が「ある」ということを実感するためには、長さや重さ、時間を表す量にきちんと正確に測れる「大きさ」がなければならないからだ。「大きさ」のない虚数で表される長さや重さなど「ある」と認めるわけにはいかない。
けれども長い間の精密な研究の積み重ねによって、虚数があることを受け入れる必然性が物理学や数学の中でそれぞれ別の理由から認められるようになった。そして虚数を使うことを前提とする量子力学と呼ばれる物理学でさまざまな現象を説明できるようになった。
しかしそれと同時に量子力学を認めることは私たちの常識的な世界観を大きく変えてしまったのだ。つまり以下に述べるような「不可解な現実」を私たちは受け入れる事態になってしまった。
量子力学で実現した物理現象の例:
- 原子内部の素粒子の運動法則が正確に導かれた。
- 化学反応を原子や電子レベルで説明できるようになった。
- 光が粒子であることの発見。これによって日焼けが起きること、星が見えることがはじめて説明できるようになった。
- 固体が硬いことを説明できるようになった。
- エレクトロニクス技術の基礎となる理論が築かれた。
- 電子の反物質である陽電子を使うことでMRIやCTなどの医療機器が開発された。
- 超伝導、超流動、レーザー光線などの技術の基礎理論が導かれた。
量子力学から導かれた「不可解な現実」の例:
- エネルギー、長さ、速度、時間にはそれ以上分割できない最小の限界がある。(プランクの量子仮説)
- 物質の位置と速度、エネルギーと時間をそれぞれ同時に正確な値で決めることはできない。(不確定性原理):その後エネルギーと時間の間には不確定性原理が成り立たないことを学んだ。「正確な時計に影響を受け、周囲の時計が不正確になることを解明 - ウィーン大」という記事を参照。
- 未来はどんなに精密に計算しても正確に予測することはできない。(関連記事)
- 1つの電子が同時に複数の場所に存在することができる。(電子の二重スリットの実験)
- 電子の位置は確率的にしか計算できない。(ボルンの確率解釈)
- 反物質や負のエネルギー、絶対0度より低い状態があること。(ディラックによる陽電子の予言)
- 完全な真空というものはないということ。(ディラックの海)
- 現在の行為が、過去の状態を変化させてしまう。(観測問題)
- 1つの粒子の変化が瞬間的に空間的に離れたもう1つの粒子に伝わる。(量子のからみ合い)
- テレポーテーションが可能であること。(関連記事)
- 時間の流れに矛盾する「原因と結果の逆転」がおきてしまう。(因果律の崩壊)
- 今の状態と別の状態が同じ空間に共存してしまう。(パラレルワールド、シュレディンガーの猫)
----------------------
2014年9月に追記:
テレポーテーションについてだが、2014年6月30日に「巨視的物体の新たなテレポート方法の開発に成功」という報告がなされた。ドラえもんの「どこでもドア」とはしくみがちがうが、巨大物体転送装置の開発への道筋が開かれたことになる。
----------------------
ちょっとの間だけお付き合いいただきたい。この不思議な現実が理解できるようになるはずだ。
---------------------------------------------------------------------
数年前「博士が愛した数式」という小説と映画が話題になった。この話の中で紹介されたのが「人類の至宝」と呼ばれる次の等式。
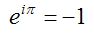
どうしてこれが人類の至宝なのだろう?小説や映画でその説明はなかった。おそらく原作者の小川洋子さんも理解されていないのだと僕は思う。
これは「オイラーの等式」と呼ばれていて、次のような「オイラーの公式」のθのところにπを代入することで得られる。
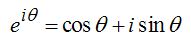
オイラーの公式は1750年頃に数学者オイラーによって導かれたもので、増加や減少を表す指数関数と回転や振動を表す三角関数が虚数 i を仲立ちとすることで、とてもシンプルかつ美しく結びついている。これは「世界一美しい公式」と呼ばれていて、その証明はこのページに書かれている。(テイラー展開を使わない証明はこのページに書かれている。)
オイラーの公式を立体的なグラフにすると次のようになる。複素数空間で螺旋を描いている。この螺旋を実数平面、虚数平面に投影すると、三角関数の波のグラフになっているのがわかるだろう。
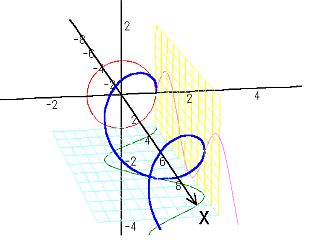
時が経つことオイラーから170年。物理学の世界では原子などのミクロな世界の現象を説明する量子力学の研究がはじまっていた。量子力学は相対性理論や電磁気学では説明できなかった、さまざまな現象を正確に説明することができ、多くの物理学者によって支持、研究されていた。
けれども量子力学はそれまでの常識ではとらえどころのない不可解な理論だった。不可解だからといって、それが間違いだということではなく、むしろその不可解さを認めることでミクロな世界の物理現象がより正確に説明できたのだ。
量子力学はEMANの量子力学のサイトや岡部先生のサイトで学ぶことができるので、いつか挑戦してみてほしい。
実は量子力学も虚数 i を使うことで成り立っている理論なのだ。4つほど例をあげて紹介しよう。
その1)パウリ行列
電子のスピンの状態はパウリが考案した次の行列を使って計算するとうまく説明できる。電子のスピンは磁気の発生や「量子のからみあい」によるテレポーテーションの原理と密接に結びついている。3つ目の行列で虚数 i が使われている。

その2)ハイゼンベルクの行列力学
量子力学の電子の運動状態の遷移を行列を使って計算したのがハイゼンベルクだ。以下のような数式で表される。
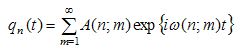
exp{iω(n;m)t} というところは e の指数関数なので、この式には「オイラーの公式」の左辺がそのまま含まれている。虚数はもちろんのこと「世界一美しい公式」がこの理論の根本原理として必要なのだ。
この行列から計算を進めてハイゼンベルクは、次の式で表される「不確定性原理」を導くことができた。
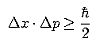
この式は「運動量pと位置xを同時に正確に決定できない。」ことを示し、また別の式から「エネルギーEと時間tを同時に正確に決定できない。」ということも導いた。
つまり「不確定性原理」はミクロの世界で、物質が存在することを正確に決定できないこと、存在している時刻や物質のエネルギーも正確に決定できないことを示している。
ハイゼンベルクの不確定性原理の影響がマクロな世界にあらわれることを紹介するために「鉛筆はどれくらいの時間立っていられるか?」という記事を書いた。ミクロの世界の物理法則に虚数 i が含まれていることと鉛筆が倒れることにはつながりがあるのだ。ぜひお読みいただきたい。(ブログ記事)
3)シュレディンガーの波動方程式
ハイゼンベルクが行列力学を使って量子力学を発展させたのに対して、シュレディンガーは波動方程式を使って量子力学を発展させた。後にディラックによってこれら2つの方法が数学的に同等であることが証明された。シュレディンガーの波動方程式は次のようなものだ。ここにも虚数 i が使われている。この方程式が量子力学の基本方程式とされていてψの部分が波動関数だ。
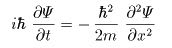
そして、この方程式は微分方程式なので具体的な条件を与えると、波動関数ψについて解くことができる。その一例は次のようなものだ。
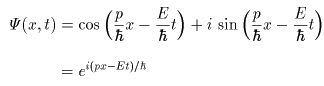
これは虚数と「オイラーの公式」そのものだ。
4)球面調和関数
太陽の周りを公転する地球がひとつの平面内を運動するのに、原子核の周りをまわる電子はどうして立体的な軌道を描くのだろうという疑問を持ったことはないだろうか?
この記事冒頭の掲載画像のように、電子は立体的な雲のような形で原子核の周りを動き回り、その正確な位置は確率的にしか予測できないのだ。(ボルンの確率解釈)
その理由を解く鍵がひとつ上で紹介した「シュレディンガーの波動方程式」にある。この方程式を電子の運動にあてはめると、次の球面調和関数であらわされる式となるのだ。そして「オイラーの公式」の左辺が含まれている。
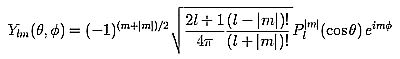
球面調和関数を解いて立体的に描くと電子の軌道はつぎのように表示される。
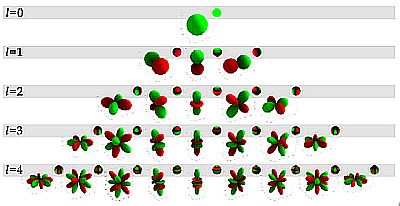
量子力学はもともとプランクが「エネルギーはそれ以上小さくできない単位」から成り立つと提唱した「量子仮説」から発展した。量子力学での物理量はすべて飛び飛びの(離散的な)値になる。電子の軌道が同心球状の殻をつくることも原子核からの距離が離散的であるためだ。この離散的な値のそれぞれを量子数と呼んでいる。
量子数には4つの種類がある。原子核から電子殻までの距離は「主量子数 n」で表され、「軌道角運動量(電子の公転)」という物理量が「方位量子数 l」で、そのほか電子のスピンは「スピン角運動量(電子の自転)」という物理量は「磁気量子数 m」表される。
これらの量子数がシュレディンガーの波動方程式から導かれ、電子の軌道配置をあらわすことになる。電子の方位量子数と磁気量子数の組み合わせのそれぞれに球面調和関数が対応し、いろいろな電子雲の立体図形が描けるのだ。(Javaアプレットによる具体例)

このうち「方位量子数」で決定されるのが、原子核を座標原点と考えたとき3次元的な方向を意味するオイラー角を示し、これが飛び飛びな離散値をとるので、電子の軌道は特定の方向にだけ伸びた立体的な配置をとることが説明できるようになる。
電子が立体的な「存在確率分布の雲の状態」で原子核のまわりに配置するため、分子の形も立体的になり、それは物質が立体的な形で存在することの根源的な理由となっているわけだ。話をもとに戻せば虚数 i を受け入れたからこそ、この世界にある物質が形を成していることが説明できる。このあたりのことを詳しく学びたい方はこのページを参照してほしい。
さらに原子から分子へと視点を移すと、分子の中で電子がどのような配置で存在しているかが理論的に計算できるようになった。(「分子軌道法: 物理学と化学の境界」)
上で紹介した「不可解な現実」は、すべて虚数を受け入れた量子力学から自然に導かれた結果だ。テレポーテーションも原子レベルでは実現されているし、ディラックが予言した陽電子も医療機器に応用されている。これらの不可解な現象を否定する根拠を私たちはもっていない。
つづく
関連記事:
複素世界は実世界とつながっている
https://blog.goo.ne.jp/ktonegaw/e/b060d7aed8c03454f25fdf81ca69c446
虚数や複素数に大小がないのはなぜ?
https://blog.goo.ne.jp/ktonegaw/e/398b0d7e84eb491dea9c38a15e994256
複素数 a+bi のプラス記号は「足す」という意味?
https://blog.goo.ne.jp/ktonegaw/e/e29c7f0e787464693ff26ab287b34ddd
応援クリックをお願いします!

関連書籍と記事:
虚数の情緒:中学、高校生にお勧め
https://blog.goo.ne.jp/ktonegaw/e/27155c8d7b5242d7e69e00335411acc1
オイラーの贈り物:高校生、大学生にお勧め
https://blog.goo.ne.jp/ktonegaw/e/fd87442dfc1b3dc7561fb5fdd72bff13

























こんなにも広大な「虚数の世界」があるとは、知りませんでした・・・!!
虚数が世界の本当の真実まで描き出してしまうなんて・・。全然「虚」なんかじゃないですね。
「不可解な現実」・・・。原因と結果の逆転?同じ空間の共存?過去の行為を変える!??・・・・・・・えええっっっ?どれ一つ取っても、ワクワクせずにいられないような話題ばかりですね・・・どうやら本当の真実は、実は私たちの日常の感覚とは遠くかけ離れている所にあるのは間違いないようですね。
ある意味、その謎を解く「チャンス」を与えられている人類は幸福なのかも・・。
また、数学・物理の勉強意欲が上がってしまったようです。。(笑)
おお!ビビッと反応していただけましたね!(笑)
嬉しいです。
趣味で学ぶ物理学や数学は、理解できなところはとりあえず飛ばして先に進むといいです。
なぜなら知識の吸収というのはジグソーパズルのように、断片的であってもピースが埋まっていくうちに、そのうちすべてがつながって絵が出来上がるようなものです。完成したときどのような絵が出来上がるか楽しみですね。
相対性理論も量子力学もそれぞれ奥が深いので理解できると深い感動と高揚感が得られますよ。その前提となる古典力学(ニュートン力学)の世界だけでも次のページのように十分に自然の不思議を経験できますし。
「理科復活プロジェクト」始動!
http://blog.goo.ne.jp/ktonegaw/e/c08cbe47b0a5ce8c64549d913800cb0a
高校物理のウソ: 物体の放物運動
http://blog.goo.ne.jp/ktonegaw/e/cc925e947c10e1a8ce17075357c8dd6e
暑さに負けずに、どんどん先に進みましょう!
考えてみれば僕とミネルヴァさんの間で電子が直接行き来しているわけではないのに、こうやって交流できていることも不思議ですね。
こんばんは。
「話題の本」のコーナーにあるということは、それはおそらく数学書ではなく、小説ですね。
この本だと思いますけど。正解ですか??
http://www.amazon.co.jp/gp/product/images/4336035938/sr=1-2/qid=1216911239/ref=dp_image_text_0?ie=UTF8&n=465392&s=books&qid=1216911239&sr=1-2
ポール・J・ナーイン
「虚数の話」(新訳版)青土社
です。
私には、かなり難解ですね~
僕の予想はハズレてしまいましたね。(笑)
なるほど、この数学の啓蒙書だったわけですか。
http://www.amazon.co.jp/gp/product/images/4791758307/ref=dp_image_0?ie=UTF8&n=465392&s=books
コーシーの話題を取り扱ってることから想像すると確かに難しそうです。アマゾンのカスタマーレビューを読むかぎり、翻訳が直訳調で読みにくいのもわかりにくい原因になってるかもしれませんね。
書店でこの「虚数の話(ポール・J・ナーイン著)を立ち読みしてきました。
確かにこれは複素関数論を勉強してからでないと歯がたちませんね。内容的に奥が深く、少なくとも理系の大学生でないと理解できない本ですね。「啓蒙書」のレベルを超えていると思いました。
こういう本が、一般の書店のフロントエンドに置いてあるというのはかなり不思議ですね。
とねさんの新シリーズを待つことにします(笑)
> こういう本が、一般の書店のフロントエンドに
> 置いてあるというのはかなり不思議ですね。
表紙が親しみやすい絵柄なので、書店の人が数学入門書か一般書だと勘違いしたのでしょうね。(笑)
見かけは親しみやすいですが、内容のレベルは大学の教科書並みです。
とねさんが、この本を読んで、平たく説明したブログの記事を書いてくれるかな~と(笑)