
物理学系や工学系であれば教科書や科目のタイトルを見るだけで内容が想像できるが、大学で学ぶ数学の内容は高校生や理数系の大学1年生、そして専門外の人にとってわかりにくいものだ。
シリーズ物の記事として大学の数学ではどういうことを学ぶかを紹介してみよう。今日の記事では目次レベルで全体像を示すことにした。次回以降の記事ではそれぞれの分野を高校生でもイメージできるように日常的な言葉を使って詳しく紹介する予定だ。数学科に進学しようと思っている高校生や物理学系、工学部系の大学生に役に立ててもらえると思う。
全体的におよそ学ぶ順番というのはあるのだが、学年が進むにつれて各分野はネットワークのように関連してくるため、本当のことをいうと1次元的な順序だてや樹形図のように分類することはできないのだ。あらかじめそのことはご承知おきいただきたい。
また、数学科の授業のタイトルは、分野の名前そのものがつけられているわけではないのでご注意いただきたい。たとえば3、4年次の微分方程式論の講座は「解析学2」とか「解析学特論」とかいう講座名だったり、複素関数論や関数解析の授業に「応用解析特論」いう講座名がつけられたりする。講座名のつけかたは学校によってまちまちだ。履修選択をするときは講座名だけで判断せず、内容や教科書、担当教官の専門分野まで確認したほうがよい。
同じタイトルの教科書であっても、入門者用と中級者用ではレベルやカバーしている範囲が違うので注意したほうがよい。
もし、不足している分野、科目があったらアドバイスいただきますようお願いします。
大学の数学は主に「代数学系」、「解析学系」、「幾何学系」、「情報処理系」、「その他」に大別される。1、2年次は比較的きれいに分類できるが、3、4年次になるとそれらが渾然一体に絡み合っているものがあるため、一概にどの分類に含まれるかを決めることができない。
数学科1、2年次に学ぶこと
1、2年次には高校数学の延長として「計算方法を学ぶ」スタイルの分野と、厳密な証明を与えて数学理論を構築する「大学の数学っぽい」分野からカリキュラムが構成されている。ほとんどが必須教科で、一部選択教科となる。
1)代数学系
線形代数(多次元行列や複素数の行列、ベクトルの計算、行列式、連立一次方程式、トレース、固有値と対角化) :計算方法を学ぶ
代数学(群論の入門):理論を学ぶ
線形代数学入門のための教科書談義
https://blog.goo.ne.jp/ktonegaw/e/9d2ac30c9f5f620ad703304d710ed90b
2)解析学系
微分積分学(複素関数論、複素積分、常微分方程式、ラプラス変換も含む):理論と計算方法を学ぶ
解析学(実関数の微積分、広義積分、多変数の微積分、特殊関数など):理論を学ぶ
注意1:「複素関数論」は「関数論」や「複素解析」と呼ばれることもある。
注意2:言うまでもないことだが「解析学」は物理学科で学ぶ「解析力学」とは全く違う分野だ。
解析学入門のための教科書談義
https://blog.goo.ne.jp/ktonegaw/e/22c325e49cfd7c721679dbc2896b86a4
なっとくする複素関数:小野寺嘉孝
https://blog.goo.ne.jp/ktonegaw/e/de4d9ea37c56d434505002d35e0132bf
3)幾何学系
位相・位相空間(集合論をベースにして位相空間を定義し、そこに成り立つ定理を学ぶ):理論を学ぶ
グラフ理論:理論を学ぶ
ベクトル解析(微分形式を使った線形代数。力学や電磁気学などで利用される物理数学):理論と計算方法を学ぶ
注意1:ここでいう「位相・位相空間」と3、4年次で学ぶ「位相幾何学」とは全く違うので注意。位相幾何学は位相空間論をベースにした幾何学のこと。また「位相解析」は「関数解析」のことなので「位相・位相空間」とも違う分野だ。
注意2:数学の「位相空間」と物理学の「位相空間」は全く違う概念なので注意。
4)情報処理系
コンピュータ入門(計算機の理論や実習、線形計画法や微分方程式の数値解法)
5)その他
統計学(基礎的な内容、各種の検定や推定):計算方法を学ぶ
論理と集合(論理学の基礎、集合論):理論を学ぶ
*物理数学について
これらの数学分野のうち、物理学科や工学部系の教科に対してのツールとして使われる分野が「物理数学」と呼ばれているものだ。これには線形代数、微積分、微分方程式、複素関数論、特殊関数、ベクトル解析、テンソルなどが含まれる。群論は通常物理数学には必要ないが、素粒子の標準理論を学ぶ際にはリー群論や群の表現論が必要になるので1、2年次には群論だけでも学んでおいたほうがよい。
EMANの物理数学
http://eman-physics.net/math/contents.html
物理数学を学ぶための本を探したい方は右のリンクからどうぞ。(Amazonで検索してみる)
数学科3、4年次以降に学ぶこと
3、4年次以降は選択教科となる。厳密な証明を与え、理論としての数学を構築、展開する。この段階になると各分野の内容は渾然一体に絡み合っているものがあるため、一概にどの分類に含まれるかを決めることができないのだが、およその目安として分類してみた。
後日追記:この記事をお読みになったhamanoboさんが現代数学の各分野の関係を示した図をコメント欄を通じて公開してくださいました。元のPDFはこちらです。より多くの方に見ていただけるよう、ここに紹介させていただきます。hamanoboさん、ありがとうございました。
画像クリックで拡大

そしてこれはTwitterで見つけた画像。クリックで拡大する。

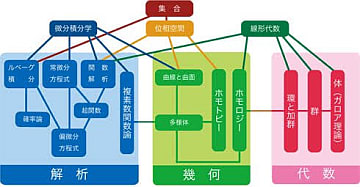
1)代数学系
代数学(群論、加群、環論、体論、ガロア理論、数論、可換体論、リー群論、群の表現論、テンソル代数、作用素代数、圏論など)
代数幾何学
注意1:「加群」というのは「加法群」のことではなく、ベクトル空間の一般化である。(ベクトル空間:体上の線型空間→加群:環上の線型空間)
注意2:「代数幾何学」は高校で学ぶ「代数・幾何」ではない。
2)解析学系
微分方程式論(常微分方程式、偏微分方程式の理論、非線形微分方程式)
関数解析(無限次元の関数空間・線形代数である。位相空間論をベースに解析学を理論的に一般化、発展させる。バナッハ空間、ヒルベルト空間、ソボレフ空間、作用素環論、フーリエ解析、関数方程式、積分変換、積分方程式)
超準解析
注意:「関数解析」は「位相解析」と呼ばれることもある。位相解析のほうが古い呼び方。
ちょっと気になる常微分方程式の本
https://blog.goo.ne.jp/ktonegaw/e/779e59b0996c582373308c0a4facf16f
3)幾何学系
微分幾何学(曲面論、微分形式、多次元微分幾何学、リーマン幾何学、射影幾何学、接続理論)
位相幾何学(多次元のトポロジー、ホモロジー、ホモトピー、コホモロジー)
微分位相幾何学(1950年代にミルナーによって創始された。大学院以上の研究分野)
多様体(実多様体、複素多様体、複素幾何)
4)情報処理系
プログラミング、コンピュータ概論、情報理論
5)その他
確率論、確率過程論(ルベーグ積分、測度論をベースに確率論、確率過程論を構築する)
統計解析(1、2年次に対してより発展的な内容、因子分析、多変量解析など)
数学基礎論:メタ数学(数学自体を数学を使って研究する分野)、ゲーデルの不完全性定理
*物理数学について
3、4年次以降に学ぶ数学の分野を昔は抽象数学、純粋数学とか現代数学と呼んでいたが、一般相対性理論や量子力学以降の現代物理学と密接なかかわりを持つことが明らかになり、もはや抽象数学や純粋数学とは呼べなくなっている。物理学科の学生にとってこれらの現代数学は「物理数学パート2」ということになるだろう。
一般相対性理論や量子力学、場の量子論、ゲージ理論を理解する目的のためだけならば、物理学の教科書だけでよいのだが、数理物理的に、つまり物理法則の背後にある数学的な裏付けや数理構造を知るためには、このような現代数学を学ぶ必要がでてくるのだ。そして超弦理論に至っては微分幾何学や位相数学(トポロジー)、複素多様体の知識は欠かすことができない。
僕は数学科卒なので物理学科および工学部の学生や先生方が、どこまで数学を学んでいるのかは知らない。人それぞれというところが本当のところだろう。不足している分野を独学している人も多いと思う。
ここで「3、4年次以降」と書いたのことに注意してほしい。3、4年次と大学院で学ぶ分野には明確な線引きができないため、僕があげたものの中には一部大学院で研究する分野も含まれている。
また数学科の学生は3、4年次でこららの分野の中から一部を選択して履修するわけなので、すべてを学んでいるわけではないことをおことわりしておく。
さて次の記事は「実用数学編」である。
関連記事:
『数学ガイダンス2016』数学セミナー増刊:日本評論社
https://blog.goo.ne.jp/ktonegaw/e/20e4c86d6279ba015ba36e0e79953bf5
理系インデックス
http://rikei-index.blue.coocan.jp/
よくわかる物理数学の基本と仕組み
https://blog.goo.ne.jp/ktonegaw/e/f4860b933fb8596cfc1c6f197ec02892
物理数学の直観的方法〈普及版〉 (ブルーバックス):長沼伸一郎
https://blog.goo.ne.jp/ktonegaw/e/ab9396e295687179ac3a71553b8165a1
理論物理学のための幾何学とトポロジー I:中原幹夫
https://blog.goo.ne.jp/ktonegaw/e/ef0b2fcb7c87aabfcd68bbe2a567840e
理論物理学のための幾何学とトポロジー II:中原幹夫
https://blog.goo.ne.jp/ktonegaw/e/9fd93716929786316ee234a66ec4d32b
ゲージ理論とトポロジーの年表
https://blog.goo.ne.jp/ktonegaw/e/1050f5ac88c40f83f566ba52c142c565
超弦理論に至る100冊の物理学、数学書籍
https://blog.goo.ne.jp/ktonegaw/e/d37fe65a84df23cca2af7ecebb83cfc6
大学で学ぶ数学とは(実用数学編)
https://blog.goo.ne.jp/ktonegaw/e/975ad3faa2f6fd558b48c76513466945
線形代数学入門のための教科書談義
https://blog.goo.ne.jp/ktonegaw/e/9d2ac30c9f5f620ad703304d710ed90b
解析学入門のための教科書談義
https://blog.goo.ne.jp/ktonegaw/e/22c325e49cfd7c721679dbc2896b86a4
ちょっと気になる常微分方程式の本
https://blog.goo.ne.jp/ktonegaw/e/779e59b0996c582373308c0a4facf16f
目次情報: スミルノフ高等数学教程 全12冊
https://blog.goo.ne.jp/ktonegaw/e/d26e1bf0916344802c90d785c535149f
ブログ執筆のはげみになりますので、1つずつ応援クリックをお願いします。




























加えるに、組み合わせの経験として何かをやっとけば、必要が出来た時に何でも勉強できます。
前もって充分な知識を用意するなんて考えてたら、いつまでたっても終わりません。
確率統計なんて仕事で必要になって勉強したけど、線型代数とルベーグ積分が分かってれば楽なもんでした。
コメントありがとうございます。
そうですよね。数学科以外の学生ならば必要な分野だけを必要になったときに学べばよいと思います。
この記事を読んで恐れおののいてしまった人がいるかもしれませんが、「大学で学ばなければならない数学」ではなく「大学で学ぶことができる数学」とお考えになっていただきたいです。
その時はコメントに対するコメントの必要があるか判断が微妙だったので、放置してしまったのですが、もし気を悪くさせてしまってたらスミマセンでした。
その後もちょくちょく記事(ブックレビューとか)を読ませていただいています。
とねさんは数学科卒だったのですね。
ぼくも数学科卒です。
さて、本題ですが、記事の中の、
1,2年次の数学基礎論というところで、少し驚きました。
素朴な集合論と論理はスタンダードだと思いますが・・・。
どこか教えている大学があるのでしょうか?
お久しぶりです。その後もブログをお読みいただき、ありがとうございます。
本題についてですが理科大理学部数学科の1年次のカリキュラム表に「論理と集合」とあったので、勢いあまって「数学基礎論」も含めてしまいました。しかしよく考えてみると、ふくちゃんがおっしゃるのが正しいと思います。1年次で学ぶのは「論理学の初歩」だけですね。数学基礎論(メタ数学、不完全性定理など)は3、4年次以降のほうに移動させました。
ご指摘ありがとうございます。
なるほど、「数学図鑑」ですか!
私たちの大学生時代はインターネットがありませんでしたが、大学の授業のタイトル情報を得ることができませんでしたが、今ではどの大学でも受験生に向けて公開しています。大学時代、どの授業を履修しようか情報不足で困っていましたので、このような記事を書こうと思いつきました。大学のホームページから得られる以上の内容を書きたいと思います。
次回以降の記事のスタイルについてもイメージが固まってきました。大学数学を学ぶのは確かに難しく、辛抱強さが要求されますが、それにも増して、こんなに深いこと、スケールの大きいことを学ぶのですよ、ということが伝わるような記事にしたいと思います。内容の厳密さにとらわれると、高校生にとってはどんどんわかりにくくなってしまいますので、ざっくばらんに自分の感じていることを紹介しようと思います。
学生時代に断念した現代数学の勉強を再開してみようと思い、数年前からほぼ独学で勉強を続けております。(歩みは亀よりも遅いです。)
とねさんのblogやtwitterは折に触れ拝見させていただいておりまして、大変参考になります。
URLに示した図は、8年前に「今後の勉強の指針にしよう」と思って作ったものです。
現代数学にどんな分野があるかがようやくわかり始めた時点に作ったものなので、おそらく誤りがあるかと思うのですが、例えばこんな図があると大学の数学あるいは現代数学を勉強しようとする私を含めた初学者には大きな助けになると思いましたので恥ずかしながら提示させていただきます。
ご参考までに。
こんにちは。貴重な関係図を公開してくださり、ありがとうございました!
極めていない分野が多いので僕にとっても大いに参考になります。
記事本文でも紹介させていただきますね。
とねさんの「数学図鑑」は、数学科への進学を考えている高校生にも、新入生の履修登録の際にも(今年度は少し遅くなってしまいましたが)、素晴らしい手引きになることでしょう。私も、どこまで出来るかわかりませんが、彼ら彼女らに負けないように頑張りたいと思います。
どういたしまして。
この記事は4月初旬に書こうと思っていたのですが延び延びになってしまいました。
今後も続きの記事を書いていきたいと思います。