足し算がわかれば引き算はその反対をすればいいので、楽でしょう
一番簡単な例として、49-26 から始めます
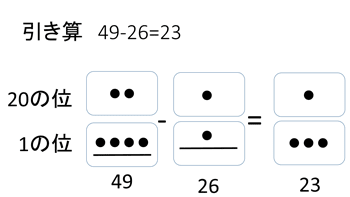
引き算ですこし最初ややこしいのは繰り下がりがあること
下のルールを確認します 1×5は5 5×4は20(桁が一つ上がって1になります)

繰り下がりのある引き算の例として 145-78 を示します

145の20の位の5および1の位の5を分割し、20の位の1を1桁下げて5×4にすることによって答えが出ました
さていよいよ掛け算
たとえば86×72では左のように筆算しますが、この中身は中のようになります

これを一般化したのが右の図、10進数(A×10+a)(B×10+b)ですが、20進数の場合は(A×20+a)(B×20+b)になります
マヤ風に縦書きにすると

演算例として1年365日の46年分の日数を計算します(うるう年は入れない)

分解すると

基本的に九九は覚えなくてもいいのですが、5×5だけは覚えたほうがいいでしょう 20の桁に1、1の桁に5が1本です
まずabです 6は5と1に分割して勘定したほうがいいです 1の成分は赤で、5の成分は緑で表しています

aBはBの●3つの成分と、棒3本の成分をわけると勘定しやすいです

Abは5が2つあると考えると早いです

ABは18が2つあると考えると早いです

以上4つを足し合わせると、16790 ご名算

コンピューターは1と0で計算しますが、マヤ文字は1と5と0で計算します
前回も書きましたが、アラビア数字のように桁で表現すること、空白の桁は0で表現することが複雑な計算を可能にしていると言っていいでしょう
マヤはたまたまこういう書き方をしたため、天文学的計算が可能になったのか?
複雑な計算をするために、このようは表記の仕方をするようになったのか?
たぶん前者でしょうね
一番簡単な例として、49-26 から始めます

引き算ですこし最初ややこしいのは繰り下がりがあること
下のルールを確認します 1×5は5 5×4は20(桁が一つ上がって1になります)

繰り下がりのある引き算の例として 145-78 を示します

145の20の位の5および1の位の5を分割し、20の位の1を1桁下げて5×4にすることによって答えが出ました
さていよいよ掛け算
たとえば86×72では左のように筆算しますが、この中身は中のようになります

これを一般化したのが右の図、10進数(A×10+a)(B×10+b)ですが、20進数の場合は(A×20+a)(B×20+b)になります
マヤ風に縦書きにすると

演算例として1年365日の46年分の日数を計算します(うるう年は入れない)

分解すると

基本的に九九は覚えなくてもいいのですが、5×5だけは覚えたほうがいいでしょう 20の桁に1、1の桁に5が1本です
まずabです 6は5と1に分割して勘定したほうがいいです 1の成分は赤で、5の成分は緑で表しています

aBはBの●3つの成分と、棒3本の成分をわけると勘定しやすいです

Abは5が2つあると考えると早いです

ABは18が2つあると考えると早いです

以上4つを足し合わせると、16790 ご名算

コンピューターは1と0で計算しますが、マヤ文字は1と5と0で計算します
前回も書きましたが、アラビア数字のように桁で表現すること、空白の桁は0で表現することが複雑な計算を可能にしていると言っていいでしょう
マヤはたまたまこういう書き方をしたため、天文学的計算が可能になったのか?
複雑な計算をするために、このようは表記の仕方をするようになったのか?
たぶん前者でしょうね









