今回は、いよいよ、カーのブラックホールについてです。
シュワルツシルトとライスナー=ノルドストロームの解が発表されてから約半世紀が過ぎた1963年に、ニュージーランド生まれの物理学者ロイ・カーが、強力な重力を持ち、高速で回転する物体のアインシュタイン方程式の解を発見しました。カー・ブラックホールのペンローズ・ダイアグラムを下の図1に示します。
このカー・ブラックホールには、三つの特徴があります。図1の左側を見ると解りますようにリング状の特異点、負の時空領域、負のCTL(Closed Time Link)領域、つまり負の閉じた時間の環の三つです。また、ライスナー=ノルドストロームのブラックホールと同様に、時間的特異点とペーパードール・トポロジーもあります。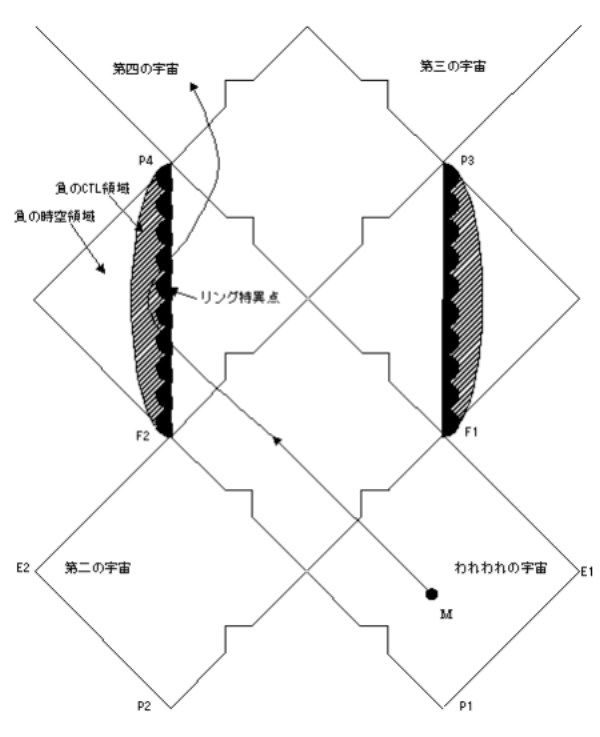
図1:カー・ブラックホールのペンローズ・ダイアグラム
まず最初は、リング状の特異点ですが、カー・ブラックホールには、特異点が点ではなく、回転軸を取り巻くリング状の形をしています。このため、無限に湾曲した領域を避けて、ブラックホールの中心に到達できるのですペンローズ・ダイアグラムでは、リング状特異点をギザギザの歯ではなく、丸い歯で表現しています。
次に、負の時空領域は、ブラックホールのリングの中心を通り抜けたところ、そこは元の宇宙ではなく、負の時空領域となっています。そこでは、G×r(Gは宇宙の重力定数、rは中心からの距離)が負になります。
中心からの距離が負になるというのは考えにくいので、重力が負になると考えられます。つまり、ブラックホールの中心に達するまでは、引っ張られる力を受けていたのですが、中心を通り抜けるとブラックホールから反発する力を受けるようになるということです。
そして.最後の三つめですが、リング状特異点の内側には、負のCTL領域、つまり負の閉じた時間の環が生じます。
リングの中心を通り抜けて、回転軸の周りを回転方向に回ると過去にさかのぼることができ、その回った回数によってどれだけ時間をさかのぼるかが決まります。そして、リングの中心を再び通って戻ると正の時空領域に戻ることはできますが、一方通行の膜があるので元の宇宙に戻ることはできず、別の宇宙へ抜けるはずです。
この別の宇宙とは、われわれの宇宙の離れた領域かもしれないし、パラレルワールドになっていて、われわれの宇宙とそっくりの別の宇宙かもしれないのです。
ロイ・カーが回転するブラックホールの解を発表してから2,3年後、ピッツバーグのエズラ・ニューマンとその同僚が、電荷を持ち回転するブラックホールの解を発表しました。今度は、カー=ニューマン・ブラックホールのペンローズ・ダイアグラムを下の図2に示します。
正のCTL領域が追加された形となっていることが解ります。この図2では、リング状特異点を通り抜けなくても、正のCTL領域に到達できるのです。この正のCTL領域により、負の時空領域を通過することなく、過去にさかのぼることができます。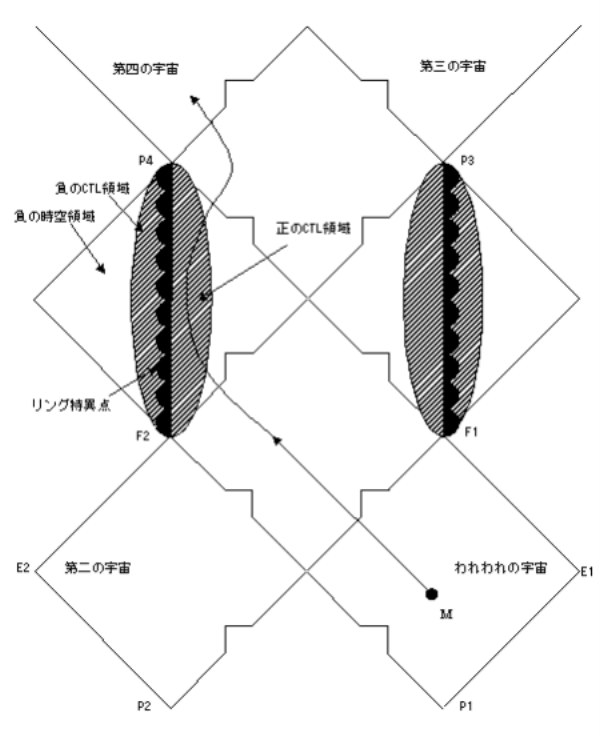
図2:ー=ニューマン・ブラックホールのペンローズ・ダイアグラム
上の図から解りますが、リング状特異点の内側には、正のCTL領域つまり正の閉じた時間の環が存在します。
カー・ブラックホールには正のCTL領域は存在せず、負のCTL領域しか存在しませんでした。しかも、負のCTL領域に行くにはリング状特異点の中心を通り抜ける必要があったのです。
下図3にカー=ニューマンのブラックホールのイメージ図を示します。リング状特異点に到達するまでに一方通行の膜が二つ存在しています。リング状特異点の内側領域に正のCTL領域が存在しています。リング状特異点の中心を通り抜けると負のCTL領域となり、さらに進むとそこは負の時空領域となっています(このイメージ図では想像しにくいので2図から類推してください)。正の時空領域に戻り、一方通行の膜を二つ抜けて出てくると、そこは別の宇宙となっています。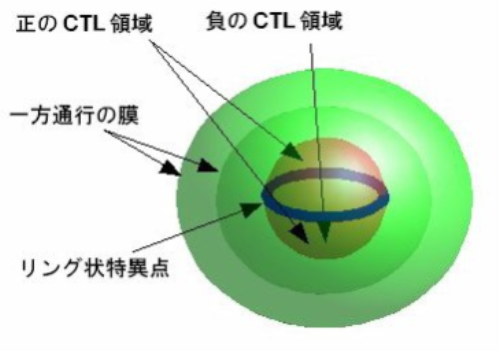
図3:カー=ニューマンのブラックホールのイメージ
カー=ニューマンのブラックホールは、リング状特異点の中心を通り抜けなくても正のCTL領域に到達できるので、そこで回転軸と反対方向に回転すると、その回った回数に応じて過去にさかのぼることができます。
ただし、一方通行の膜が存在するので、元の宇宙に戻ることはできず、別の宇宙へ行ってしまうようです。
最新の画像[もっと見る]
-
 タイムトラベルとタイムマシン?
10年前
タイムトラベルとタイムマシン?
10年前
-
 パウリの夢の数式に「虚数」が生み出された!
11年前
パウリの夢の数式に「虚数」が生み出された!
11年前
-
 「微細構造定数」137とパウリ&ユング
11年前
「微細構造定数」137とパウリ&ユング
11年前
-
 宇宙インフレーション 超弦理論
11年前
宇宙インフレーション 超弦理論
11年前
-
 拡張標準モデルとは?
11年前
拡張標準モデルとは?
11年前
-
 拡張標準モデルとは?
11年前
拡張標準モデルとは?
11年前
-
 相対性理論とローレンツ対称性
11年前
相対性理論とローレンツ対称性
11年前
-
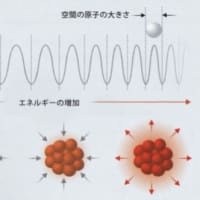
 宇宙の起源に新説か?
11年前
宇宙の起源に新説か?
11年前
-
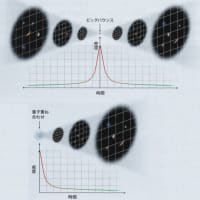
 宇宙の始まりは「ビッグバウンス」?
11年前
宇宙の始まりは「ビッグバウンス」?
11年前
-
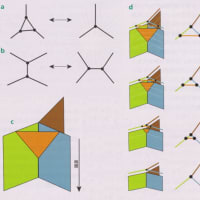 「スピンの泡」が時空に対応する、ループ量子重力
11年前
「スピンの泡」が時空に対応する、ループ量子重力
11年前










※コメント投稿者のブログIDはブログ作成者のみに通知されます