プランク長とブラックホールは同じもの？

　一般相対論の考え方では、物体が作る重力場は周りの時空を歪める。
重力場には重力半径と呼ばれる場所があって、これより内側からは何ものも、光さえも脱出不能であり、これがブラックホールと呼ばれるゆえんである。
ブラックホールは巨大な質量を持つ天体が、自分自身の重力で重力半径以下の小さな固まりに収縮してしまう際に形成されるものと考えられている。
しかし、じつはこのブラックホールは、プランク長程度の非常に小さなスケールでの現象とも密接な関係がある。

　質量Ｍの物体の重力半径ｒは、一般相対論によればｒ＝２ＧＭ／ｃ^2という式で計算できる。
アインシュタインのエネルギーと質量の等価性を考えれば、この式は大きなエネルギーが存在すればブラックホールが形成されることをそのまま意味している。
そこで、プランクエネルギーに相当する質量をこの式に代入すると、ほとんどそのままプランク長に戻ってしまうのだ。
つまり、なんと重力半径とプランク長は一致するのだ。

　これは、プランク長以下の物体はすべてブラックホールになってしまうことを意味している。
現在の素粒子理論は、電子やクォークなどは大きさがゼロである数学的な点であるものとして扱っている。
くりこみ理論が必要になった理由も、距離がゼロの場所を考えなければならないことがその原因だ。しかし実験的には、たとえば電子の大きさは１０^-19メートル以下であることがわかっているにすきず、大きさがセロであると考える理由はない。

　超弦理論の発想は、粒子に重力半径以上の大きさを持たせることで数学的な問題を取り除こうという考えに基づいている。
この理論を数学的に問題なく作り上げるには、舞台となる時空が１１次元でなければならないという面白い結論が得られている。
超弦理論は、四次元時空ではうまくいかず、特定の時空でなければ理論が破綻してしまうのだ。
逆に、これは高次元時空があるはずだと考える強い根拠にもなっている。

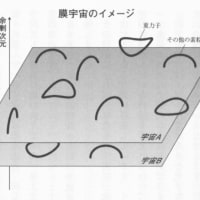
　ＡＤＤ模型は超弦理論ではないが、それによって必要とされている余剰次元という枠組みを使って大雑把に、かつ幾何学的に重力の弱きについて考察したものといえる。
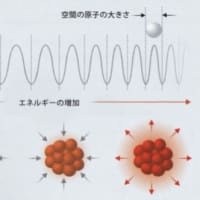
ＡＤＤ模型が考える余剰次元は、プランク長に比べて大きく広がったものだけである。
本当は超弦理論が考える１１次元時空であったとしても、そのうちの二つだけが大きく広がればよいと考えるわけだ。

　さて、ＡＤＤ模型とは、高次元でのプランクエネルギーが1テラ電子ボルト程度と仮定することでプランク長が高次元で変更される、という模型だった。
すなわち、ＡＤＤ模型をそのまま受け取れば、1テラ電子ボルトのエネルギーを集中させるとブラックホールが形成されるという結論になる。

　つまり、プランクエネルギーが修正されるという考えは、そのままブラックホールが形成されるエネルギーを修正する、という主張と読み替えることができる。
よって、ＡＤＤ模型によれば高エネルギー衝突でブラックホールが形成されることは、計算するまでもなく当たり前のことなのだ。

　ＡＤＤ論文では、このエネルギーを1テラ電子ボルトであると置いてその結論を導いているが、この高次元プランクエネルギーにしても、余剰次元の数にしても、実験と矛盾しないかぎりはどんな数値になるべきか、あまり強い制約はない。
そこで、ここではＡＤＤの考え方を一般化して、さまさまな余剰次元の数の場合に、高次元プランクエネルギーと余剰次元の大きさの関係を見てみよう。

図：一般化されたＡＤＤ模型の予想

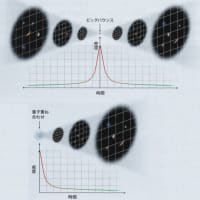
　加速器実験では、ブラックホール生成以外にも、高次元方向に重力子がエネルギーを持ち去ってしまう場合など、いくつかの余剰次元の証拠となる現象が予言されている。
ただし、いずれも高次元プランクエネルギー程度のエネルギーが注入された際に生じるものである。
一方、加速器による方法以外でそもそもの重力の法則の修正をまともに検証することも、もちろん正攻法として考えるべきだ。
この場合には、余剰次元の大きさよりも小さな距離で逆二乗則が破れることがその証拠となる。
すなわち、キャベンディシュの実験を、ミリメートル以下の近距離で行えばよいのである。
ＡＤＤの仮定した1テラ電子ボルトという高次元プランクエネルギーの値には、はっきり言ってあまり強い根拠は感じられない。
しかし、そのスケールに未知の重力現象が発見され、ＡＤＤの発想に基ついて現在の物理学が抱えている階層性問題や、力の統一といった究極の課題を一気に解決に導く可能性があるのは確かだ。
これは素晴らしいアイテアだ。

　この論文が出て以来、多くの高エネルギー物理学者はこの問題に興味を持ち、ＬＨＣでの余剰次元の証拠探しを始めた。
理論の論文も、ほとんどは加速器実験での信号に関するものである。
一方で、逆二乗則の直接検証の持つ能力は魅力的である。
たとえば、ＬＨＣは最大で陽子同士が14テラ電子ボルトのエネルギーで衝突するが、実際には陽子の中のクォーク同士が衝突するものと考える必要がある。
すると、衝突しなかった残りのクォークはそのまま飛び去るので、衝突エネルギーの一部しか、じつはブラックホール生成などに利用することができない。

　陽子内部にはクォークが三つあるので、利用されるエネルギーはだいたい14テラ電子ボルトの3分の1程度である。
すると、ＬＨＣの能力は最大でも5テラ電子ボルト以下の高次元プランクエネルギーの探索に限定される。
実際には、たとえわずかながらブラックホールが生成されたとしても、その他の現象による膨大な雑音に信号が埋もれてしまって見えにくくなるので、もっとずっと感度は制限されるだろう。

　さて、5テラ電子ボルトの高次元プランクエネルギーは、余剰次元の大きさに換算すると80ミクロンである。
仮に、1ミクロンでの逆二乗則の直接検証が可能であれば、逆に高次元プランクエネルギーに換算して40テラ電子ボルトにもなる高エネルギー領域を探索できることになる。
ミクロンスケールでのキャベンディシュの実験が、ＬＨＣをはるかに超える超高エネルギーの物理の探索能力を持っていることに驚く。

　もし、ブレーンのシナリオが正しければ、我々は本当の高次元の宇宙を知らずに、その中の狭く薄い三次元世界を宇宙だと信じ込んできたことになる。
カリレイが自ら発明した望遠鏡を使って、地上の世界から宇宙空間の姿とその広がりを見たように、我々はまさに今、自ら発明した装置を駆使することで、三次元ブレーンから重力の望遠鏡を使って、本当の高次元宇宙を覗き見ようとしているのだ。