八元数が、弦（ひも）と膜（ブレーン）と次元に関係？

　私たちは量子力学が真実であることを知っている。そして量子力学によると、粒子は波でもある。物理学者が毎日使っている標準的な3次元の量子力学では、あるタイプの数（「スピノール」と呼ばれる）が物質粒子の波としての動きを記述する。別のタイプの数（「ベクトル」と呼ばれる）は力の粒子の波動を記述する。粒子の相互作用を記述するには、これら2つを一体として扱うために急ごしらえの乗算のようなものを使う必要がある。いま現在採用されている系はうまく自然界を記述するが、とうてい洗練されたものではない。

　その代わりとして、空間だけで時間のない奇妙な宇宙を考えよう。この宇宙の次元が1または2、4、8である場合、物質粒子と力の粒子のどちらも、その波動が1種類の数によって記述されるようになる。つまり、ある多元体に属する数、加減乗除の演算が可能な
体系に属する数によって記述可能になる。言い換えると、これらの次元ではベクトルとスピノールが同じもの（数）で記述される。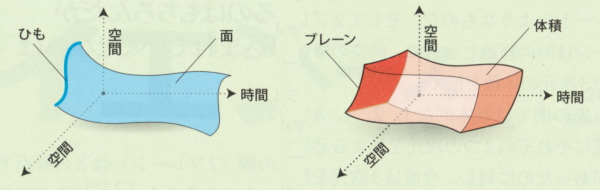


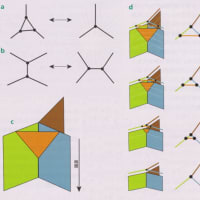
図：弦（ひも）と膜（ブレーン）と次元
超弦理論では、1次元の「ひも」が時の経過とともに2次元の面を描く。M理論では、2次元の膜（ブレーン）が同様に3次元の体積を描く。これらの次元を八元数の8次元に加えると、超弦理論とM理論がなぜ10または11の次元を必要とするかについて、手がかりが得られる。


　1次元宇宙の物質粒子と力の粒子は実数で記述され、2、4、8次元宇宙の場合はそれぞれ複素数と四元数、八元数が対応する。こうすると超対称性が自然に現れ、物質と力を統一的に記述できるのである。相互作用は乗算によって明快に記述され、すべての粒子は（物質も力も）、同じ数体系を使って表現される。

　しかし、実際には時間を考慮に入れる必要があるので、このオモチャの宇宙は現実ではありえない。時間を考えた場合、超弦理論では興味深い効果が生じる。ひもはどの時点においても1次元の存在で、曲線や直線のようなものである。だが、ひもは時の経過とともに2次元の面を描く（上図参照）。この広がりによって次元が2つ加わる（ひもの1次元と時間の1次元）ことで、超対称性が生じる次元が変わってくる。時間のないオモチャ宇宙で超対称性が生じるのは1、2、4、8次元だったが、時間のある宇宙では3、4、6、10次元で超対称性が生まれることになる。

　一方、超弦理論の研究から、同理論では10次元の宇宙だけが自己矛盾のないものになるとされている。その他の次元では、同じことを計算しても計算方法によって結果が異なるものになる「アノマリー」という異常が生じるのである。10次元でないと超弦理論は破綻してしまう。そして10次元の超弦理論は、いま述べたように八元数を用いる超弦理論である。

　つまり、超弦理論が正しいなら、八元数は単なる役立たずの珍品ではない。それどころか、八元数はこの宇宙がなぜ10の次元を持っていなければならないか、その深遠な理由を提供している。10次元では、物質の粒子と力の粒子が同じタイプの数、ほかならぬ八元数で体現されるのである。

　しかし話はこれで終わりではない。物理学者は近年、1次元のひもだけでなく、より高次元の膜（メンブレーン）を研究するようになった。例えば2次元の膜（2ブレーン）はどの時点でもシートのようなものである。そして2ブレーンは時の経過とともに、時空のなかで3次元の体積を描く。

　先の例では基本的な1、2、4、8次元にそれぞれ2つの次元を加える必要があったのに対し、今度は3次元を加えなくてはならない。したがって、ブレーンを扱う場合には、4、5、7、11の各次元で超対称性が自然に出現するはずである。そして先の場合と同様、超弦理論の発展型であるM理論（MはメンブレーンのM）では宇宙に11次元が必要とされる。やはりここでも八元数が自然に求められるようなのである。

　ただ残念ながらM理論は未完成で、基本的な方程式さえもまだ書き下されていない（その意味でMはミステリアスのMでもある）。この理論が将来どのような形を取ることになるか、正確に述べるのは困難である。

　現時点では、超弦理論とM理論が実験的に検証可能な予言をまだ何もしていないことを強調しておくべきだろう。どちらの理論も美しい夢ではあるが、いまのところ夢にすぎない。私たちが住んでいる宇宙は10次元や11次元には見えないし、これまでのところ物質粒子と力の粒子の間に何らの超対称性も見られてはいない。

　超弦理論の優れた専門家であるグロスは、欧州合同原子核研究機構（CERN）の大型ハドロン衝突型加速器LHCで超対称性の証拠が見つかる可能性を50％だとみている。慎重派によると、確率はもっと低い。どうなるかは時が語ってくれるだろう。この不確実性のため、私たちが身の回りに見ている世界を理解するうえでこの不思議な八元数が基本的な重要性を持っているのか、それとも単に美しい数学的存在なのか、判明するのはまだ先である。

　数学的美それ自体に価値があるのはもちろんだが、八元数が自然の基本構造に組み込まれているとなれば、さらに愉快だろう。複素数はじめ多くの数学の歴史が語っているように、純粋に数学的な考案が後に物理学者が必要とするツールになった例はたくさんある。

　八元数がその仲間に加わる可能性は十分にあるだろう。