空間がとりうる量子状態は点と線からなる

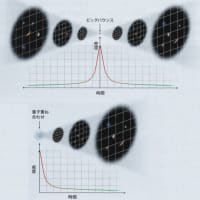
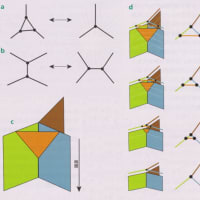
　空間の構造を非常に小さなスケールで理解するには、重力の量子論が必要になる。空間に重力が関係してくるのは、 時空（空間と時間）の歪みから重力が生じることがアインシュタインの一般相対性理論によって示されているからである。量子力学と一般相対論の基本原理を注意深く組み合わせることで、「ループ量子重力理論」が生まれた。この理論では、空間がとりうる量子状態は点と線からなる「スピンネットワーク」という、ループ量子重力や関連する理論での、量子幾何学的構造の一つの状態である。そして、節に対応する体積の量子、辺に対応する面積の量子（図１）がある。時空の量子状態は同様の「スピンフォーム」というスピン・ネットワークが時間とともに、局所的な変化の列を通じて変動する（図２）。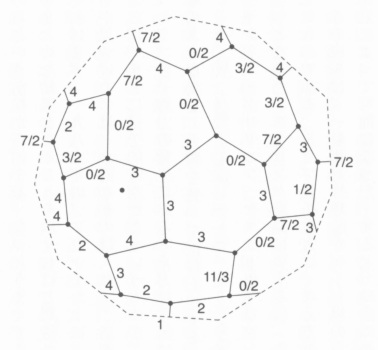


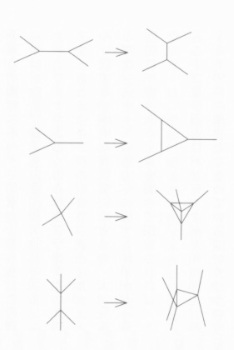
　　　　図１：スピン・ネットワーク　　　　　　　　　　　　　    　図２：スピン・フォーム


　少し前にこのブログ「http://blog.goo.ne.jp/sonokininatte55/e/d5f2ecad0738fac66d781a9aa082222b」

“迷走する物理学・・・時間を思う！”で次のように述べています。

「私は時間が要なのではないかと強く思っている。量子論と相対性理論は、時間の本性については根本のところで間違っているのではないか。そんな思いが強くなっている」

だから、「時間」と本質的に向き合って、理論を展開していると思われる、この「ループ量子重力理論」についての考察をもっと追求していきたいと思っています。

wikipediaより
・・・・
　ループ量子重力理論は、時空（時間と空間）にそれ以上の分割不可能な最小単位が存在することを記述する理論である。重力の古典論である一般相対性理論を量子化した量子重力理論の候補である。時空は、本質的に連続で滑らかな値をとるものと考えられてきたが、この理論で時空は、原子における電子配置のように離散的な値をとるものと考えられている。同じく量子重力理論の候補である超弦理論は、時空は背景場として最初からそこに存在するものとして定義しており、理論自身のダイナミクスにより決定されているわけではない。それに対しループ量子重力理論は、一般相対論と同様に理論自身が時空そのものを決定している。(背景独立性)
　空間はノード（点）とノードにつながる線を使いグラフで表される。ループ量子重力理論で使うグラフはスピンネットワークと呼ばれる。このスピンネットワークで表される空間のつながりの変化が重力などの力の媒介、電子などの素粒子の存在を示していると考えられている。そして、このスピンネットワークに時間を加えたものをスピンフォームと呼ぶ。スピンフォームは時計の秒針が動くように離散的に変化する。つながりの変化前と変化後の時間の差は1プランク秒（10^-43秒）で、これが積もり積もって人が感じる時間となる。
・・・・

　ループ量子重力理論によると、空間は個別の小さな塊からできていて、最小の塊の体積はおよそ1立方プランク長（10^-99cm3）である。時間の進みは飛び飛びで、その最小単位はおよそ1プランク秒（10^-43秒）となる。こうした時空の離散的構造から生まれる効果は、近い将来に実験で確かめられるだろう。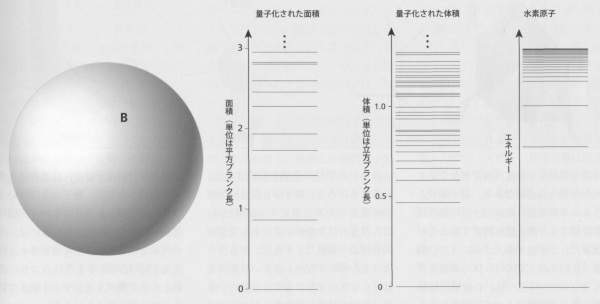


図３：体積と面積の量子状態
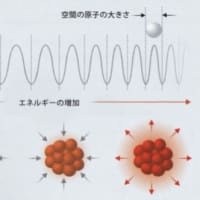
ループ量子重力理論による主要な予言の1つは、体積と面積に関するものである。図３のような球状の殻によって、空間に境界Bが定義されているとしよう。境界の内側の空間はいくらかの体積を持っている。古典的（非量子的）な物理学によると、この体積の値はどのような正の実数にもなりうる。しかしループ量子重力理論によると、体積には絶対的な最小単位があり（およそ1立方プランク長＝10^-99cm3) 、より大きな体積もこの最小単位に制限されて離散的な値しかとれない。同様に面積にも最小単位があリ（およそ1平方プランク長=10^-66cm2)、面積の値も離散的になる。面積と体積について許される量子状態の離散スペクトル（グラフの左と中央）は、水素原子の量子工ネルギー準位（右）とよく似ている。


1980年代半ば、少数の物理学者が量子力学と一般相対論の統合に再挑戦した。Ｌ．スモーリン、アシュテカ、ジェイコブソン、ロヴェッリらで、標準的な手法によって両理論を統合する可能性を改めて吟味しようと考えた。そこで、空間が滑らかで連続しているという仮定を置くことなしに計算を実行する道を探った。特に、一般相対論の2つの重要な原理を計算の中核に据えた。

　1つは「背景独立性」である。この原理は時空の幾何構造が固定したものではなく、絶えず変化する力学的な対象であることを意味する。時空の幾何構造を知るには、物質とエネルギーが及ぼすあらゆる効果を含んだ一連の方程式を解く必要がある。ちなみに、いま定式化が進んでいる超弦理論は背景独立ではなく背景依存であり、古典的な時空構造（非量子的な時空構造）があらかじめ存在するとしたうえで、弦を記述する方程式を組み立てている。

　2つ目の原理は「微分同相変換不変性」である。これは背景独立性と切っても切れない関連がある。時空とその方程式を表現するうえでどんな座標系を選んでも構わないとする原理で、一般相対論で初めて採り入れられた。時空の一点は座標値によってではなく、そこで物理的に起きている事柄のみによって定義されると考える（特別な座標系は存在しないので）。微分同相変換不変性はとても強力な原理であり、一般相対論の重要な基盤になった。

　この2つの原理を量子力学の標準的手法と注意深く組み合わせ．空間が連続的か離散的かを計算によって見極める数理的方法を編み出した。その結果、空間が量子化されていることが明らかになった。ループ量子重力理論の基礎ができたのである。「ループ」という言葉は、この理論計算が時空の中の小さなループ（閉曲線）に関連することに由来する。

　この理論は最小スケールで見た時空構造についての量子論だから、この理論の機能を説明するには、小さな体積の領域について理論が何を予言するかを考える必要がある。量子論でこうした考察を行う際には、どの物理量を計測するかを正確に特定することが重要である。そのため、1つの境界「B」によって区切られた領域を考えた。この境界は鉄製の殻など物質によって定義されたものでもよいし、ブラックホールの「事象の地平面」のように時空の幾何構造そのものによって決まるものでも構わない（事象の地平面は、ブラックホールの重力にとらえられて光さえもその内側から脱出できなくなる境界面）。

　こうした領域の体積を計測すると、どうなるだろう。量子論と微分同相変換不変性の両方を満足する結果とは、どんなものになるのか？

　もし空間の幾何構造が連続だとすると、あらゆる大きさの領域が存在しえて、計測結果はどんな正の実数にもなりうる。つまり、領域の体積を限りなくゼロに近づけていける。しかし幾何構造が離散的なら、計測結果は飛び飛びの値にしかならず、それ以上は小さくできない最小の体積が存在することになる。

　この問題は原子核の周りを回っている電子のエネルギーを問うのと同じである。古典力学では電子はどんな量のエネルギーも持ちうるが、量子力学ではいくつか特定の値しか許されない（中間的な値にはならない）。この違いは、水の流量を測るのに、水を連続体ととらえる19世紀的な考え方に立つか、それとも水を構成する原子を1個ずつ数えるかの違いだともいえる。

　ループ量子重力理論によると、空間は原子の集合体に似ており、体積の測定結果は飛び飛びの離散的な値にしかならない。空間領域は特別の離散的な体積を持つ塊として現れる。境界Bの面積はどうか。ここでも同理論に基づく計算結果は明快で、境界面の面積も離散的な値になる。つまり、空間は連続ではない。面積と体積には特定の量子単位がある。

体積と面積が取りうる値は「プランク長」という単位で測られる。この長さは重力の強さと量子の大きさ、光速に関連しており、空間の幾何構造がもはや連続的に記述できなくなる距離の目安となる。プランク長は非常に小さく、10^-33cmである。最小の面積はプランク長の2乗で10^-66cm2, 最小の体積は同じく3乗で10^-99cm3 となる。

　1cm3の空間に“体積の原子”が約10^99個も存在するわけである。この体積量子は非常に小さく、1cm3中に10^99個という数字は観測可能な全宇宙に体積1cm3の立方体をびっしり詰め込んだ数（10^85 個）を上回る。