「レベル4マルチバース」

　レベル1から3までのマルチバースでは、初期条件や物理定数はそれぞれ異なりうるものの、自然を支配する基本法則は同じである。しかし、そこで打ち止めにする必要があるだろうか。

　自然法則そのものが違う宇宙があってもよいのではないか。量子効果が存在せず、古典物理学の法則に従う宇宙などというのはどうだろう。時間が連続したものではなく、コンピューターのクロック信号のように離散的なステップを踏んでやってくる宇宙なんていかがだろうか。何もない空っぽの12面体の宇宙というのもありかもしれない。レベル4マルチバースでは、これらすべてが実在する。このてのマルチバースの存在が予想されるのは、抽象的な理論の世界と観測された実世界との間に厳密な対応関係があるためである。

　私たちの世界は数式、より一般的には数やベクトル、幾何学図形といった数理的構造によって非常な迫真性をもって記述できる。物理学者のウィグナーが1959年に行った有名な講義の中で、「自然科学において数学が桁外れの実用性を発揮しているのは、ある種の神秘といえる」と語った。裏返していえば、数理的構造が得体の知れない現実感を伴っているということである。

　数理的構造は客観的な存在であり、誰が研究しても同じ結論になるという客観的存在としての条件を満たしている。証明ずみの定理は、それを証明したのが人間であれコンピューターであれ、あるいはお利口なイルカであっても、真実である。思慮深い宇宙人がいるなら、彼らも私たちと同様に同じ数理的構造を見いだすに違いない。数学者たちがふつう数理的構造を「創造した」とはいわず、「発見した」と表現するのもこのためである。

　数学と物理学との対応関係をどう理解するかについては、2つのパラダイムがある。いずれももっともだが、まったく相反する見方で、おそらくプラトンとアリストテレスの時代から意見が分かれてきたであろう。

　アリストテレス哲学の見方によれば、根本は物理的実体であって、数学的表現は単なる便利な近似にすぎない。一方のプラトン哲学によると、数理的構造こそが真の実体であり、観測者はそれを不完全な形でしか認識できない。これらは、どちらの視点がより基本的なのか、観測者という“蛙の視点”と物理法則という“鳥の視点”のどちらを基本的と見るかの違いである。アリストテレスは蛙の視点を、プラトンは鳥の視点を重視する。

　私たちはみな、数学について何も知らない子どものころに、アリストテレス的な見方に慣らされている。プラトン的な見方は後に身につくものである。しかし、現代の物理学者たちはプラトン的見方に傾いている。数学によって宇宙をこれほどうまく記述できるのは、宇宙そのものが本来、数理的であると考えられるためである。

　とすると、あらゆる物理現象は詰まるところ数学の問題だということになる。無限の知力と力量を持つ数学者がいたなら、原理的には“蛙の視点”を計算できるだろう。その宇宙が内に含んでいる自意識を持つ観測者とは何なのか、その観測者が何を認識しているのか、彼らが認識内容を他者に伝えるためにどんな言語を考案するか、といった事柄までも計算できるだろう。

　数理的構造は不変の抽象的実在であり、空間や時間に縛られない。もし歴史が映画のようなものなら、その構造は映画のワンシーンではなく、一巻のビデオテープに相当する。

　ここで、3次元空間の中を動き回る点のような粒子でできあがっている宇宙を考えてみよう。4次元時空の中では（鳥の視点に立てば）、これらの粒了の軌跡はもつれたスパゲティのように見える。蛙からは粒子が等速運動して見える場合、鳥の視点からはゆでる前のスパゲティのような1本の真っ直ぐな軌道が見える。蛙からは2個の粒子が対になって回転して見える場合、鳥に見えるのは二重らせんのようにもつれ合う2本のスパゲティとして見える。

　蛙にとっては、世界はニュートンの運動方程式と万有引力の法則によって記述される。しかし、鳥にとっては、スパゲティの幾何学的配置、つまり1つの数理的構造が世界の記述となる。蛙そのものもゴチャゴチャした一塊のパスタにすぎず、その非常に複雑な絡み合いが情報を蓄積・処理する生体としての粒子集団を表している。私たちの宇宙はこの例よりもはるかに複雑で、どのような数理的構造が対応しているのかはまだわかっていない。

　さて、プラトン的パラダイムに立つと、「宇宙が現在のような宇宙になったのはなぜか」という疑問が持ち上がる。アリストテレス学派にとっては、これは意味のない問いである。宇宙は現に存在するものでしかない。しかし、プラトン学派の立場からは、宇宙がいまとは違う宇宙にならなかったのはなぜかと問わずにはいられない。宇宙が数理的なものなら、多くの数理的構造からどうして特定の1つだけが選ばれ、宇宙を記述するようになったのかは、実存の最も本質的なところに、基本的な非対称性が組み込まれているように思えてしまう。

　この難問を回避するため、数理的な対称性は完全に保たれ、あらゆる数理的構造が物理的にも存在するものと考える。それぞれの数理的構造が宇宙に対応し、全体としてマルチバースを形作る。このマルチバースを構成する個々の要素は同じ空間には存在せず、空間と時間を超えた存在となる。おそらく、内部に観測者を含まない宇宙が大半であろう。

　この仮説はプラトン的な考え方を究極にまで突き詰めたものといえる。プラトンのイデアの世界にある数理的構造、あるいは数学者ラッカーのいう「マインドスケープ」が物理的にも存在するというわけである。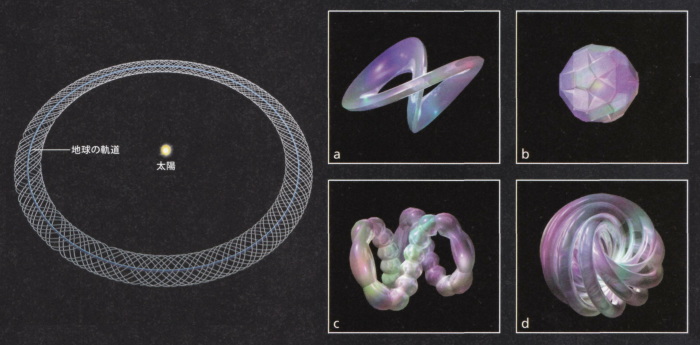


図：数理的構造そのものが宇宙「レベル４マルチバース」
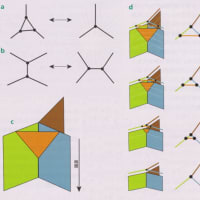
究極の並行宇宙はあらゆる可能性を含む。その位置や宇宙論的な特性、量子状態が異なるだけでなく、物理法則までが異なる宇宙の存在が考えられる。これらの宇宙は空間と時間を超えたところにあるので、目に見えるように描くのはまず不可能である。最良の方法は、抽象的に思い描くこと。宇宙とは、それを支配する物理法則の数理的構造を表現した「彫刻」のようなものといえる。例えば、1つの単純な宇宙を考えよう。地球と月、太陽があり、ニュートン力学に従っているとする。客観的立場の観測者からは、この宇宙は組み紐で覆われた丸い輪のように見える（丸い輪は地球の軌跡、それを覆う組み紐は地球を周回する月の軌跡）。物理法則が異なれば、宇宙の形も異なってくる（a~d)。この考え方に立つと、物理学の根本にかかわるさまざまな問題が解決する。

　マルチバースの階層構造はレベル4でおしまいになる。基礎的な物理理論が自己矛盾のないものならば、これらはいずれも何らかの数理的構造によって表現可能だからである。

　レベル4マルチバースの仮説は実証可能であり、レベル2マルチバースの場合と同様、レベル4マルチバースは1つの集合（この場合は数理的構造の全体）と選択効果を含んでいる。数理的構造の分類が進むにつれ、私たちの世界を記述している数理的構造が観測結果と一致する最も一般的な構造であることが判明するだろう。同様に、私たちが将来に観測する事柄は過去の観測事実と首尾一貫した一般的なものになるはずで、過去の観測事実は私たちの存在と矛盾しない最も一般的なものである。

　「一般的」が何を意味するかを定量的に示すのは難しい問題で、その研究は緒についたばかりである。しかし、数理的構造には1つの顕著で有望な特徴がある。私たちの宇宙が明快で秩序を持っているのは数理的構造の対称性と不変性のおかげであるが、これらは例外なく一般的だという点である。数理的構造にはもともとこうした特徴が備わっているようで、この特徴を取り除くには複雑な公理を付け加える必要がある。


　ここまで紹介してきたように並行宇宙には4つの階層があり、レベル1からレベル4へと向かうにつれて私たちの宇宙とはかけ離れたものになる。レベル1では宇宙の初期条件が異なるだけだが、レベル2では物理定数や粒子にも差が生じ、レベル4に至っては物理法則そのものが異なる余地がある。私たちの宇宙と質的に変わりがないのはレベル3だけで、過去数十年にわたってレベル3宇宙の考え方が反論の嵐に見舞われてきたのは皮肉なことである。

　今後数年で、宇宙マイクロ波背景放射や大規模スケールでの物質分布など宇宙論に関連する観測が劇的に進むとみられ、空間の曲率と位相幾何学的性質がもっと正確に突き止められることにより、レベル1宇宙の仮説に白黒がつくだろう。こうした観測を通じてカオス的永久インフレーション理論を検証することにより、レベル2宇宙を調べることもできるだろう。宇宙物理学と高エネルギー物理学の双方が進歩すれば、物理定数がどの程度まで微調整されたかが明確になり、レベル2宇宙が存在するのかしないのか、可能性が絞り込まれてくるはずである。

　量子コンピューターの研究開発が実を結べば、レベル3宇宙の新たな存在証明となる。量子コンピューターは基本的に、並列計算にレベル3宇宙の並行性を利用するものだからである。一方では「ユニタリー性の破れ」を探す実験も進みつつあり、もしもこの証拠がつかめた場合、レベル3宇宙は存在しないことになる。

　そして最終的には、一般相対性理論と場の量子論の統合という現代物理学最大の難問が解決されるかどうかで、レベル4宇宙に対する見方が大きく左右される。私たちの宇宙に厳密にマッチする数理的構造が見つかるか、あるいは数学的に理不尽な壁にぶつかってこの仮説を放棄せざるをえなくなるかのいずれかとなる。

　だから、私たちも並行宇宙の存在を信じてみてはいかがだろうか。これに対し、並行宇宙に関する議論は何の役にも立たないうえ、いかにも奇妙すぎるという反論もある。決して観測できない世界を仮定するなど、「オッカムのかみそり」（「最も単純な説明が最良である場合が多い」とする原則）に照らしても説得力を欠く。異なる世界が無限に存在するほど、自然は浪費家ではないはずである。

　しかし、この議論は裏を返すと、マルチバースの存在を支持することにもなりうる。自然が本当に浪費しているのは何だろう。空間や質量、原子などではないのは確かである。レベル1マルチバースにしても、すでにこれらを無限に含んでいるのだから、そのほかに少しくらい無駄にするものがあっても何の問題にもならない。重要なのは、単純明快さが損なわれるかどうかである。

　全体集合はしばしばその構成要素よりも単純な場合がある。例えば整数全体の集合を考えよう。全集合と1つの数字のどちらが単純だろうか。素朴に考えると、数字1つのほうが単純に思える。しかし、整数全体を生成するコンピュータープログラムはとても簡単で、これに比べると大きな数1つを記述するほうがずっと長い行数を占めることもある。実は全体のほうが単純なのである。

　同様に、アインシュタインの場の方程式に対する解の全体集合は、個々の解よりも単純で、一般解はいくつかの方程式で表現できるが、個々の解を求めるには、ある超曲面上での膨大な初期値を特定する必要がある。つまり、集合の中の特定の要素に関心を絞ると複雑さが増し、すべての要素をまとめ上げていた全体性に本来備わっていた対称性や単純さが損なわれてしまうということである。

　この意味では、高レベルのマルチバースほど単純である。私たちの宇宙に比べ、レベル1マルチバースは特別な初期条件を設定する必要がないという点で単純である。そして、レベル2では物理定数を特定する必要もなくなり、レベル4になると一切を特定しなくてよくなる。一見すると豊かな複雑さも、すべては観測者（蛙の視点）が主観的に認識するものの中にある。鳥の視点に立てば、マルチバースほど単純なものはない。

　マルチバースの概念が奇妙すぎるという不満は、科学というよりは美意識の問題だろうし、そもそもアリストテレス的世界観に立った場合だけに問題となるものである。奇妙だからといって、では何だというのだろうか。実在の本質に迫る深遠な問いに対する答えが、奇妙なものではないとでもいうのだろうか。私たちは遠い祖先から今日に至るまで、日常の物理現象に関する直観を育んできた。進化の過程で、それが生存競争に有利だったからである。逆にいえば、日常世界をひとたび離れれば、奇妙に見える事柄を予測するほうがむしろ当然といえよう。

　4つのマルチバースに共通する特徴は、並行宇宙に本来備わっている単純さと、おそらくはこれ以上明快なものはないといえるほど鮮やかな理論である。これら宇宙の存在を否定するには、実験的に確かめられていないプロセスや場当たり的な仮定を加えるなどして、理論を複雑にしなくてはならない。例えば、空間が有限であるとか、波動関数が収縮するとか、存在論的な非対称性などを持ち込まねばならなくなる。

　結局のところ、無駄であか抜けしないのはどちらなのかという判断になる。たくさんの世界と、たくさんの論争のどちらを選ぶかである。おそらく私たちは、私たちの宇宙が奇妙であることにだんだんと慣れ、その奇妙さが魅力の一部であることに気づくだろう。