
※スカイプ体験授業で解説しています。
※色々なレベルに合わせた十数種類以上の教材をご用意しております。
※数理科学の発想・思考トレーニングも実施中。

※スカイプ体験授業で解説しています。
※色々なレベルに合わせた十数種類以上の教材をご用意しております。
※数理科学の発想・思考トレーニングも実施中。
<問題>

<類題>
戦略で学ぶ数学・数と式 数学の発想のしかた
スカイプ無料体験授業:整数
<コメント>
教科書を中心とした標準問題をまずマスターし、その後、ややレベルが高い融合問題にも習熟しておこう。
nが正の偶数のとき、2^n-1 は3の倍数であることを示せ。
nを自然数とする。2^n+1 と 2^n-1 は互いに素であることを示せ。
p,qを異なる素数とする。2^(p-1)-1=pq^2 を満たすp,qの組をすべて求めよ。
<問題>

<解答>

<コメント>
誘導のない大問を解ききる練習が不可欠である。整数や確率などの京大入試で頻出の分野も出題されており、
「離散的なもの」を扱う分野の対策は特に入念に行っておきたい。
次の2つの条件を同時に満たす四角形のうち面積が最小のものの面積を求めよ。
a.少なくとも2つの内角は90°である。
b.半径1の円が内接する。ただし、円が四角形に内接するとは、円が四角形の4つの辺すべてに接することをいう。

※スカイプ体験授業で解説しています。
※色々なレベルに合わせた十数種類以上の教材をご用意しております。
※数理科学の発想・思考トレーニングも実施中。
1から25までの整数がひとつずつ書いてあるカードが25枚ある。これをよくきって、1枚ずつ2回ぬきとる。最初にぬきとったカードをもとに戻してよくきってから次のカードをぬきとる場合を「戻す場合」といい、最初のカードを戻さずに次のカードをぬきとる場合を「戻さない場合」ということにする。最初にぬいたカードに書いてある整数をaとし、次にぬいたカードに書いてある整数をbとする。1.戻さない場合、a+b=8 となる場合の数を求めよ。2.戻す場合、550<ab<600 となる場合の数を求めよ。(センター)
200から800までの整数のうち、8の倍数全体の集合をA、12の倍数全体の集合をBとする。1. n(A),n(B) を求めよ。2. n(A∩B), n(A∪B)を求めよ。(広島女子大)
5個の数字0,1,2,3,4から3個の数字を選んで3桁の整数を作る。このうち、偶数は何個か。(神奈川大)
0,1,2,・・・,9の札が各1枚ある。これらを並べて5桁の数をつくるとき、56789以下の5桁の数はいくつあるか。(武蔵大)
男女4名ずつ、合計8名の男女がいる。1つの円卓で会食するために、この8名の座席を抽選によって決めたい。このとき、男女が交互に座る場合の数を求めよ。(明治大)
大人2 人と子供4 人が,円形の6 人席のテーブルに着席するとき,大人2 人が隣り合わないような並び方は何通りあるか.
アルファベットの大文字Aが3つ、小文字aが3つある。1.これら6文字を1列に並べて得られる異なる文字列は全部で何個あるか。2.6文字のうち、3文字を1列に並べて文字列を作るとき、異なる文字列は全部で何個あるか。(日大)
赤球1個、白球2個、黒球2個の計6個のじゅず順列の総数を求めよ。(法政大)
internetのすべての文字を使ってできる順列のうち、どのtもどのeより左側にあるものは何通りか。(南山大)
A,B,C,D,E,F,G 7人を並べる方法のうち、A,B,Cの3人が隣り合うものは全部で何通りあるか。(西南大)
5個の黒石と4個の白石をよく混ぜてから1列に並べる。どの2つの白石も隣り合わない並べ方の総数を求めよ。(お茶大)
男子5人と女子4人がいる。この9人を、3人ずつの3室へ入れる。ただし、部屋には区別をつけない。このとき、次の問いに答えよ。1.はいり方の総数を求めよ。2.各室に女子が少なくとも1人入る方法は何通りあるか。(兵庫医大)
5個の玉を3つの箱A,B,Cに分配する方法を考える。空箱ができてもよいとして、次の問いに答えよ。1.玉に1から5の番号がうってあるとき、分け方の総数を求めよ。2.玉に区別がつかないとき、分け方の総数を求めよ。(早稲田)
5個の玉を3つの箱A,B,Cに分配する方法を考える。どの箱にも1個は玉を入れるとして、次の分け方の総数を求めよ。1.玉に区別がないとき 2.玉に区別があるとき(慶応)
5個の玉を区別がない3つの箱に分配する。どの箱にも1個は玉を入れるとして、次の場合の分け方の総数を求めよ。1.5個の玉に区別のあるとき 2.5個の玉に区別のないとき(明治)
いくつかの10円玉、50円玉、100円玉を用いて1400円を作りたい。このときの作り方は何通りあるか。ただし、用いる個数は0個でもよいとする。(慶応)
ある市場調査に300人のモニターが回答し、家電製品A,B,Cを持っているかどうかが調べられた。Aを持ってる人、Bを持ってる人、Cを持ってる人はそれぞれ、100人、120人、130人であった。3種類とも持っている人は10人、3種類とも持っていない人は60人であった。どれか2種類だけ持っているのは何人か。(立教)
8個の異なる品物をA,B,Cの3人に分ける方法を考える。1.Aが少なくとも1個の品物をもらう分け方は何通りか。2.A,B,C がいずれも、少なくとも1個の品物をもらう分け方は何通りか。(筑波)
1辺の長さがnの正方形の各辺をn等分した網目状の図形を考える。この図形に含まれる線分を辺とする四角形の個数を求めよ。
方程式 x+y+z=28 を満たす非負整数の組 (x,y,z) の個数を求めよ。(東海大)
方程式 x+y+z=28 を満たす正整数の組 (x,y,z) の個数を求めよ。
次の問いに答えよ。1.正5角すいの各面を赤、青、黄、緑、白、黒の6色すべてを使って色を塗るとき、何通りの塗り方があるか。
2.正5角柱の各面を赤、青、黄、緑、白、黒、茶の7色すべてを使って色を塗るとき、何通りの塗り方があるか。(龍谷大)
立方体の各面に、異なる6色をすべて使って、色を塗りたい。ただし、立方体を回転させて一致する塗り方は同じとみなす。何通りの塗り方があるか。(鹿児島大)
集合x={1,2,3,・・・,9,10}の部分集合の個数を求めよ。(浜医大)
さいころを4回投げてk回目に出た目を ak (k=1,2,3,4) とする。1.a1<a2<a3<a4 となる目の出方は何通りあるか。2.a1≦a2<a3≦a4 となる目の出方は何通りあるか。(福岡大)
1から9までの9個の数字から、相異なる3個を用いて作られる3桁の整数の総和を求めよ。(日本女子大)
箱の中に白玉4個、青玉6個入っている。この箱の中から4個の玉を同時に取り出すとき、その中に白玉2個、青玉2個入っている確率を求めよ。
3つのさいころを投げるとき、すべて異なる目が出る確率を求めよ。
5つのさいころを投げるとき、すべて異なる目が出る確率を求めよ。
10個の白玉と20個の赤玉が入った袋から、でたらめに1個ずつ玉を取り出す。ただし、いったん取り出した玉は袋へは戻さない。このとき、n回目にちょうど4個目の白玉が取り出される確率pnを求めよ。ここで、nは4≦n≦24を満たす整数である。
箱の中に1から10までの整数が1つずつ書いてある10枚のカードが入っている。この箱から1枚のカードを取り出し、その数を読んで、元に戻してよくかき混ぜる。この試行を3回繰り返したとき、取り出したカードに書かれている数について答えよ。1.最大値が7である確率を求めよ。2.最大値が7で最小値が3である確率を求めよ。
甲、乙2つのさいころを同時にふるとき、甲のさいころの目が乙のさいころの目より大きくなる確率を求めよ。
さいころをn回投げるとき、k回目に出る目の数をxkとし、yn を x1,x2,・・・,xn の積とする。yn が3の倍数でない確率を求めよ。
さいころを繰り返しn回ふって、出た目の数をかけ合わせた積をXとする。すなわち、k回目に出た目の数をykをとすると、X=y1y2y3・・・yn が成り立つ。Xが6で割り切れる確率qnを求めよ。
7人の男子と5人の女子合わせて12人のグループがある。次のA.B.の順で4人の委員を選ぶ。A.最初にくじにより3人の委員を決める。B.Aの結果3人とも男子であった場合には、残り1人の委員は女子の中からくじで決める。3人とも女子であった場合には、残りの1人委員は男子の中からくじで決める。それ以外の場合には、残りの1人の委員をまだ委員になっていない9人の中からくじで決める。このとき、次の問いに答えよ。1.男女各2人ずつが委員となる確率を求めよ。2.男子1人女子3人が委員となる確率を求めよ。
さいころを投げるゲームをする。1の目が出たら得点を1点、2または3の目が出たら2点、その他の目が出たら0点とする。1点または2点をとったときは続けてさいころを投げ、0点を取った時点でゲームを終了する。合計得点が3点でゲームが終了するとき、3回目でゲームが終了する確率を求めよ。
かたよりのあるA,B2つのタイプの硬貨を考える。Aタイプの硬貨は表の出る確率が1/100、裏が出る確率が99/100で、Bタイプの硬貨は表の出る確率が99/100、裏が出る確率が1/100である。袋の中に、Aタイプの硬貨99枚、Bタイプの硬貨1枚が入っている。袋の中から硬貨を1枚取って投げたとき、表が出たものとする。このとき、その硬貨がAタイプの硬貨である確率を求めよ。
7本のくじのうち、1本だけ当たりくじがある。A,Bの2人が当たりが出るまで1本ずつこの順で交互にくじを引き続けるとき、Aの当たる確率を求めよ。ただし、引いたくじはもとに戻さないとする。
7本のくじのうち当たりくじが2本ある。
淳、敦、武の3人がこの順に元に戻さないで1本ずつくじを引くとき、淳、敦、武がそれぞれ当たる確率を求めよ。
7本のくじのうち当たりくじが3本ある。このくじをまず淳が2本引き、次に武が2本ひく。
ただし引いたくじは元に戻さないとすると淳、武がそれぞれ1本ずつ当たる確率を求めよ。
正四面体ABCDの4つの頂点を移動する点Pがある。
点Pがいずれの頂点にあるときも1ステップ後に同じ頂点にとどまる確率は2/5であり、
他の頂点に移動する確率はいずれも1/5である。
頂点Aから出発した点Pがnステップ後に頂点Aにある確率をa(n)とする。(n=0,1,2,・・・)
1.a(n)をa(n-1)で表せ。(n=1,2,3,・・・)
2.数列a(n)の一般項を求めよ。(富山大)
ある町の住人を任意に3人選んで1,2,3と番号をつけ、それぞれの人の生まれた曜日を調べる。ただし、町の人口は十分多く、その中でどの曜日に生まれた人も同じ割合であるとする。3人のうち少なくとも2人が同じ曜日生まれであるという事象をA、1番の人が日曜日生まれであるという事象をBとする。事象AとBとは独立であることを示せ。
あるクラスの学生の通学方法をしらべたところ、バスを利用している人が30名、自転車を利用している人が20名、バスも自転車も利用していない人が12名であった。このクラスの学生から任意に1人選び出すとき、その学生がバスの利用者であるという事象をA、自転車の利用者であるという事象をBとすると、AとBは独立事象であった。次を求めよ。1.全学生数を求めよ。2.P(A)、P(A∪B)
A,B,Cの3チームが野球のリーグ戦をすることになった。・AがBに勝つ確率は、2/3。・AがCに勝つ確率は、1/5。・BがCに勝つ確率は、3/4。Aが1勝1敗する確率を求めよ。(埼玉大)
動点Pは、硬貨を同時に2枚なげて、2枚とも表が出れば座標平面上をx軸の正の方向に1だけ動き、1枚が表で他の1枚が裏のときはY軸の正の方向に1だけ動き、2枚とも裏のときは動かないものとする。いま、動点Pの出発点を原点(0,0)とし、硬貨2枚を3回投げたとき、点Pが点(2,1)にある確率を求めよ。
袋の中に白玉、赤玉、黒玉が1個ずつ入っている。袋から無作為に玉を1個取り出し、白玉ならAの勝ち、黒玉ならBの勝ち、赤玉なら引き分けとする。取り出した玉をもとに戻し、このゲームを繰り返す。A,Bのうち、先に3回ゲームに勝った方を優勝とするとき、5回目のゲームでAの優勝が決定する確率を求めよ。
1個のさいころを100回続けて投げるとき、1の目がn回出る確率をp(n)で表すことにする。ただし、nは0≦n≦100なる整数とする。次の問いに答えよ。1.p(n)の値を、nを用いて求めよ。2.nが0≦n≦100なる整数nのとき、p(n)<p(n+1)なるnの値の範囲およびp(n)>p(n+1)なるnの値の範囲をそれぞれ求めよ。3.0≦n≦100なる整数nのうち、p(n)の値を最大にするようなnの値を求めよ。
xy平面上の原点にある点pは、硬貨4枚を同時に投げて、表が3枚以上出たときはx軸の正方向に1進み、表が2枚または1枚出たときはy軸の正方向に1進み、表が出ないときは動かないものとする。いま、硬貨4枚を同時に投げるという試行を3回行った。1.pが点(1,2)にくる確率を求めよ。2.pが点(1,1)にくる確率を求めよ。
ある人が4人の友人宛に4通の手紙をかき、4枚の封筒にこれら4人のあて先をかいた。手紙の内容やあて先は1人1人すべて異なっている。これらの手紙を1通ずつ無作為に封筒に入れるとき、X通だけ正しいあて先の封筒に入ったとする。Xを確率変数とみて、確率分布表を作れ。また、Xの期待値を求めよ。
区別のできる2つのさいころA,Bを同時に投げる試行を行う。さいころAの目からさいころBの目を引いた数Xの期待値を求めよ。
mを自然数とする。区間[0,m)にごく小さな砂粒をn個でたらめに落とす実験を行った。どの砂粒についても、[0,1),[1,2),・・・,[m-1,m) のいずれの区間に落ちるかは独立で同程度に確からしいとすれば、区間[0,1)に落ちる確率は1/mである。1.n個のうち、ちょうどk個の砂粒が区間[0,1)に落ちる確率を求めよ。2.区間[0,1)に落ちる砂粒の個数の期待値を求めよ。
原点Oから出発して、数直線上を動く動点Pがある。さいころを投げて4以下の目が出たら点Pは1だけ正の方向に進み、5以上の目が出たら2だけ負の方向に進む。この試行を6回繰り返したとき、点Pの座標Xの期待値を求めよ。
袋の中に黒玉4個、白玉4個がある。この中から無作為に4個の玉を同時に取り出し、取り出された黒玉の個数を値とする確率変数をXとする。このとき、Xの分散を求めよ。(慈恵医大)
トランプのカードがn枚(n≧3)あり、その中の2枚はハートで残りはスペードである。これらのカードをよくきって裏向けに積み重ねておき、上から順に1枚ずつめくっていくことにする。初めてハートのカードが現れるのがX枚目であるとき、1.X=Kである確率pkを求めよ。(k=1,2,・・・,n-1)2.Xの平均およに分散を求めよ。(奈良医大)
1と書かれたカードが2枚、2と書かれたカードが2枚、4と書かれたカードが1枚、計5枚のカードがある。この中から2枚のカードを無作為に取り出し、それらに書かれている数の和をXとするとき、確率変数Xの標準偏差を求めよ。(滋賀医大)
<問題>

<解答>
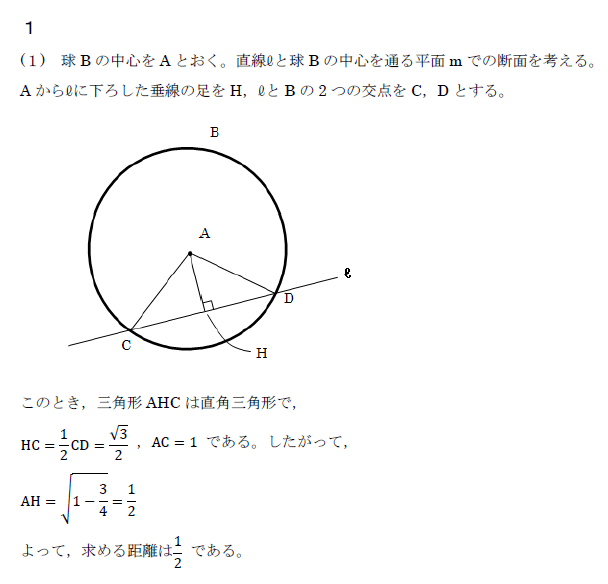
<ヒント>

<コメント>
よくある回転体の問題である。
断面図を描く→立式→計算の流れで完答したい。
やや易。
古代ギリシャ数学の伝統は近代数学に脈々と続いています. 古代ギリシャの代表的な算術書はユークリッド (Euclid, 330-275 BC) の 「原論」(Elementa) ですが, その他, ヘレニズム時代の算術書, 古代インドの算術書, 古代中国の算術書, イスラム帝国時代の算術書などと 近代数学や理論計算機科学との繋がりを眺めることは楽しいことです.
古代ギリシャのピタゴラス学派やプラトンらの数学的な蓄積を引き継いで, ユークリッド(Euclid, 330-275 BC) は紀元前300年ごろに「原論」(Elementa) を 著しました. この書物は13巻からなっており, 幾何学と数論を展開しました. 古代ギリシャ数学の集大成であった「原論」は, 幾何学や数論の経典として, 二千数百の長き間, 不朽の価値を持ち続けました. また, この書は多くの学者に研究され, 注釈されてきたばかりでなく, 学校数学の教科書として近年まで実際に使われてきました. しかし, 「原論」の形成過程についてはよく分かっていません. ユークリッドに先立って, 複数の学者達によって「原論」の編集が 行われていたという説もあります. 「原論」の第1巻は23個の「定義」, 5個の「公準」, 9個の「公理」から始まります. 第2巻~第7巻, 第10巻, 第11巻もいくつかの「定義」から始まります. 「定義」, 「公準」, 「公理」は, ギリシャ語のヒュポテシスが分化したものです. ヒュポテシスは英語のhypothesis (前提) の語源です. 「定義」が議論を進める上での共通の前提に対して, 「公準」は弁証法において, 相手が自明のこととして受け入れることに疑問があるかもしれないことを, 前提とすることを意味する用語です. 「公理」は共通概念で, 「公準」に近い意味です.
「原論」に与えられている結果は, 「定義」, 「公準」, 「公理」から演繹されたものです. すなわち, この書は, 厳密な公理的論証の体系を与えています. このような手法は, 紀元前5世紀のエレア学派の弁証法に影響されて形成されたと 考えられています. エレア学派というのは, 紀元前5世紀頃にイタリア半島南部に開花した哲学の一派で, パルメニデス(Parmenides, 515-450 BC頃) やゼノン(Zenon, 490-430 BC頃) 等に 代表されます. ヨーロッパで生まれた近代数学の厳密さは, 古代ギリシャ数学を基礎としていると云われているのは, 近代数学は「原論」に見られる公理的論証法の精神を受け継いでいると 見なされているからです.
「原論」が紀元前300年頃に世に出るや, すぐに普及しました. アルキメデス(Archimedes, 287-212 BC) などは, 「原論」に記述されている命題を巻数と番号で引用していました. 3~5世紀頃のエジプトのアレキサンドリアや小アジアでは, 「原論」の体系的な注釈本がいくつか世にでました. 8~10世紀頃のイスラム帝国黄金時代には, 「原論」はアラビア語に訳され, アラビア数学の発展に貢献しました. 11~12世紀頃に, アラビア語で書かれた「原論」がラテン語に翻訳され, ヨーロッパに伝承されました. ギリシャ語の原典から直接ラテン語に翻訳された「原論」も見つかっておりますが, 当時のヨーロッパでは, アラビア語からラテン語への翻訳本の方が普及していました. この頃のヨーロッパはいわゆる暗黒時代で, イスラム文化圏の方が, 経済, 学問などで ヨーロッパよりかなり進んでいました. 1450年にドイツ人のグーテンベルグ(Johannes Gutenberg, 1398-1468頃)が, ぶどう絞り機にヒントを得て活版印刷機を発明しました. それ以後, ヨーロッパでは宗教書や学術書の出版が盛んになり, 「原論」のギリシャ語の復刻版やラテン語の翻訳版, 各言語の翻訳版もヨーロッパの各地で相次いで出版されました. 例えば, 「原論」のドイツ語訳, フランス語訳, 英語訳, スペイン語訳は 16世紀に出版されています. 因みに, 中国語訳は17世紀に, 最も古い日本語訳は1884年に出版されました.
ユークリッドの「原論」の7巻に2つの自然数の最大公約数の求め方が 与えられています. ユークリッドのアルゴリズムといえば, この手順を指します. ユークリッドのアルゴリズムでは, 2つの自然数, r0とr1の最大公約数は 次のように求めます. r0をr1で割り, 余りがなければr1が最大公約数です. 余りがあれば, そのときの余りをr2とし, r1とr2の最大公約数を 同じ方法で求めます. すなわち, r1をr2で割ったときに, 余りがなければr2が最大公約数です. 余りがあれば, そのときの余りをr3とし, r2とr3の最大公約数を 同じ方法で求めます. このようにして, 割り算のときに余りがなくなるまで続けます. 余りはだんだん少なくなるので, このアルゴリズムによる計算はいずれ終了し, 最後の除数が最大公約数です. このアルゴリズムは再帰的な構造をしており, 計算の効率も極めてよいのです. 多くの計算機アルゴリズムの教科書には, このアルゴリズムが記述されています. 二千数百年も前に, このようなアルゴリズムが存在していたことは, 驚くべくことです.
「原論」では, 素数についても論じています. 素数が無限個あることの証明は「原論」の9巻に与えられています (命題20). 整数の中でどれだけの頻度で素数が現れるかは, 当時でも興味があったであろうと想像できますが, この問題は近代数学の時代になってからやっと解決しました. 1798年に, フランスの数学者ルジャンドル (Andrie-Maria Legendre, 1752-1777) は整数x以下の素数の数の近似値として, x/(ln x - 1.08366) を与えました.
ドイツの数学者ガウス(Johann Carl Friedrich Gauss, 1777-1855)は, ルジャンドルよりもよい近似式を与えました. ガウスの与えた近似式は, x以下の素数の数は 1/(lnx)の2からxまでの積分値です. ガウスの近似式はxが大きくなるにしたがい, 漸近的に正しい値に近づくことが予想されていましたが, その証明は難解でした. この命題は「素数定理」(Prime Number Theorem)と呼ばれ, ドイツの数学者リーマン(Georg Friedrich Bernhard Riemann, 1826-1866) も その証明に取り組みました. 彼は「リーマン予想」と呼ばれる命題を考え, それが正しいことを証明しようと試みました. その命題とは, ゼータ関数と呼ばれる複素関数に関するものです. 「リーマン予想」が正しければ, 「素数定理」も正しいことがいえます. しかし, 「リーマン予想」は解析学の難問で, 21世紀の今日でも未解決です. フランスの数学者アダマール(Jacques Salomon Hadamard, 1865-1963) と ベルギーの数学者ポアソン (de la Vallee Poussin, 1866-1962) は独立に, 「リーマン予想」を用いないで, 1896年に「素数定理」が正しいことを 証明しました.
ユークリッドはエジプトのプトレマイオス王に, 「原論」よりも手っ取り早く幾何学を学ぶ方法はないかと訊ねられ, 「幾何学に王道なし」と答えた話は余りにも有名なエピソードです. 19~20世紀に活躍したイギリスの著名な数学者であり, 哲学者であったラッセル(Bertrand Russell, 1872-1970) は 彼の自伝の中で次のように述べています. 「私は11歳のときに兄と一緒にユークリッドの原論を学び始めました. このことは, 私の人生で経験した偉大な出来事の一つです. それは, 初恋のときに味わうような目も眩むような感動でした. この世の中にこんなにも素晴らしいことが存在しようとは, それまで想像することも出来ませんでした」. 近代ヨーロッパの科学者の多くは, 彼らの少年, 少女時代に ユークリッドの「原論」を学び, 大きな感動を覚えたであろうことは, この文章からも想像できます. 近代ヨーロッパで, 自然科学や数学の分野での素晴らしい成果が次々と生まれたのも, このような下地があったからだと思います.
ユークリッドの「原論」に匹敵する書として, ディオファンタス(Diophantus, 紀元250年頃か300頃年頃)の「算術」 (Diophanti Alexandrini Arithmetica ) を上げることができます. ディオファンタスは古代ギリシャ数学の伝統を引き継ぎ, エジプトのアレキサンドリアで紀元250~300年頃に活躍し, 13巻からなる「算術」を著したこと以外は, 余りよく分かっていません. 彼が何処で生まれ, いつアレキサンドリアに来て, いつ亡くなったかもはっきり分かりません. ディオファンタスの業績は, 紀元250年頃に著された「算術」に 詳細に記述されていますが, その「算術」も6巻しか現存していません.
アレキサンドリアはプトレマイオス朝の時代から, ディオファンタスの頃までの数世紀にわたって, 学問の中心でした. 紀元前3世紀のはじめに, この地に建てられたアレキサンドリア文庫は 古代最大の図書館とされ, ヘレニズムの学問研究の拠点でした. しかし, 数度にわたる外国軍の攻撃にさらされ, 数え切れないほどの 多くの貴重な蔵書は失われました. 「算術」の6巻が生き延びたのは奇跡に近いと云われています. これらの攻撃は, あるときはキリスト教徒によるものであり, あるときはイスラム教徒によるものでした. 紀元642年, イスラム軍がアレキサンドリアを攻略したときは, 残された蔵書もほとんど焼かれたり, 破棄されたといわれています. 一部の知識人が焼け残った蔵書を アレキサンドリアからコンスタンティノーブルに移しました. ディオファンタスの「算術」もこの中に含まれていたと思われます. しかし, 災難はさらに続きます. 1453年にオスマン帝国によるコンスタンティノーブルの襲撃があり, ここでも多くの蔵書が失われました. ビザンティン帝国の学者達は貴重な蔵書の一部を運び出し, それらをヴァチカンに持ち込みました. このような受難の時期を含めて, ヨーロッパの学問は, 7世紀頃以後, 15~16世紀頃まで停滞していました. この時期の学問の中心は, イスラム文化圏やインドでした. 15世紀になって, ディオファンタスの「算術」の一部は ヴァチカンで発見されましたが, そのラテン語訳がヨーロッパで刊行されたのは16世紀になってからです. 「算術」がヨーロッパに登場したのは, それがアレキサンドリアで誕生してから, 実に約1300年も経ってからです.
「算術」には, 100余りの問題と, それらの丁寧な解答が書かれています. 問題の多くは複数個の未知数に対する, 整数係数の代数方程式の整数解を求めるものです. このような方程式のことをディオファンタス方程式といいます. ディオファンタス方程式には, 解がないかも知れないし, 解が有限個あるかも知れないし, 解が無限個あるかも知れません. 例えば, a, b, c がすべて整数で, 未知数が x と y の方程式 ax + by = c について, x と y の整数解を求める問題は, 2個の未知数についての, 1次のディオファンタス方程式です. この方程式が解をもつのは, c が a と b の最大公約数の倍数である場合で, そのときの整数解は無限にあります. このような方程式は, 一般に解が一意に定まらないので不定方程式と呼ばれています.
「算術」のラテン語訳はいくつか刊行されましたが, 1612年に, フランスの数学愛好家, バシェ(Claude-Gaspar Bachet de Meziriac, 1581-1638)のラテン語訳が よく知られています. フランスの法律家であり, 数学愛好家であったフェルマー(Pierre de Fermat, 1601-1665)は バシュ訳の「算術」を学びながら, その余白に書き込みをしていました(1637年頃). これらの書き込みは48箇所あり, その多くは数論に関する命題の形をしていました. その中の1つに, 「n > 2 のとき, xn + yn = znを満たすx, y, zの 零でない整数解は存在しない. この命題の証明を得たが, それをここに記すには余白が小さすぎる」とあります. これが世に言う「フェルマーの最終定理」です. 云うまでもなく, n=2のときは, ピタゴラスの定理から分かるように, x2 + y2 = z2 の整数解は無限個あります. しかし, n > 2について, この命題の証明は極めて難解で, 多くの数学者が挑戦しましたが, 358年間も未解決でした.
イギリスの数学者, ワイルズ(Andrew John Wiles, 1953-)は, 8年におよぶ努力の末, ついにフェルマーの最終定理の証明に成功しました. 1984年頃には, 「谷山-志村の予想」が証明されれば 「フェルマーの最終定理」は証明できることが分かっていました. しかし, 「谷山-志村の予想」の証明は極めて難しく, 大きな壁でした. ワイルズは「谷山-志村の予想」を証明することにより 「フェルマーの最終定理」を証明したのです. 彼の証明は, 20世紀の数論の手法を駆使して生まれたものです. ワイルズの証明は, 1995年刊のアメリカ数学会の雑誌, Annals of Mathematics に 掲載されました. フェルマーが「算術」の余白に残した命題(フェルマーの最終定理)は, その後の数論の目覚しい進歩のきっかけを与えたと言えます. 「谷山-志村の予想」は谷山豊(1927-1958)が, 1955年の日光での国際シンポジウムで提案した楕円方程式に関する問題を, 志村五郎(1930-)が「すべての楕円方程式はモジュラー形式と深い関係がある」 という予想に発展させたものです. 天才, 谷山豊は自ら蒔いた数学の種が見事に育っていくことを見届けないで, 31歳の若さで自らの命を絶ちました. 楕円方程式というのは, y2 = x3 + ax2 + bx + c なる形の ディオファンタス方程式のことです. ここで, a, b, cは任意の整数です. ディオファンタスは 「算術」の中で楕円方程式の性質を記述していることから分かるように, 楕円方程式は紀元3世紀ころから関心がもたれていました. それに対して, モジュラー形式は19世紀になってから, やっと数学の世界に登場しました. モジュラー形式は数学の極めて難解な領域で, ある種の対象性を持つ演算の世界です. ワイルズの貢献は, フェルマーの最終定理を証明したことよりも, 楕円方程式とモジュラ形式を結びつけた, 「谷山-志村の予想」を証明したことの方が より大きいと云われています.
ロシア生まれのドイツ人数学者, ヒルベルト (David Hilbelt, 1862-1943) は, 1900年のパリで開催された国際数学者会議で, 20世紀の数学の方向性を示す23の問題についての講演をしました. これらの問題は「ヒルベルトの23の問題」として知られており, 今日でも未解決な問題を含みます. 「リーマン予想」もこの中に含まれており, まだ解決していません. ヒルベルトの23の問題の10番目は, 「n個の未知数を含む整数係数の多項式, すなわちディオファンタス方程式が整数解をもつかどうかを判定する アルゴリズムを見つけよ」です. この問題は, 1970年にロシアの数学者, マティヤセヴィチ(Yuri Matiyasevich, 1947-) によって否定的に解決されました. すなわち, ディオファンタス方程式が整数解を持つかどうかを判定する アルゴリズムは存在しないことが示されたのです. 解の範囲を有理数に拡張すると, この問題は今日でも未解決です.
有限個の整数の世界で, 四則演算が行えるようにすることは古い時代から考えられていました. {0, 1, ,2 , ... , m-1} はm個の整数の集合です. この集合をZmで表わします. Zmの世界での加算, 引き算, 掛け算は通常の整数の世界のように計算し, 計算結果がm以上のときは, それをmで割った余りとします. また, マイナスの数はmの整数倍を加えて0以上m-1以下の数にします. Zmの世界では, 割り算は, 除数の逆数と被除数の積になります. 逆数が存在するのは, その数とmが互いに素のときです. このような計算を,mを法とする剰余計算といいます. この計算を mod m で表記します.
紀元400年頃に書かれた中国の算術書, 「孫子算経」に 「3で割れば2余り, 5で割れば3余り, 7で割れば2余るような数は何か?」 という問題があります. 「孫子算経」は古くから中国, 朝鮮, 日本で使われてきた算術書ですが, 著者は不明です. 現存する最古の版は南宋本で, 上, 中, 下の3巻からなっています. 上の問題は連立合同式, x = 2 (mod3), x = 3 (mod 5), x = 2 (mod 7) を解くことです. このような連立合同式を一般的に解く公式は19世紀にガウスによって示され, 「中国人剰余定理」(Chinese Remainder Theorem)と呼ばれています. 剰余計算は現在の情報処理, 符号理論, 暗号理論などで重要です.
律令は中国で発達した法体系です. 律令国家は律令を統治の基本法典とした国家で, 中国の隋・唐で確立し, 周辺諸国に波及しました. 日本でも7世紀半ばから形成され, 整然とした官制の下で, 多くの官僚がこれを支えました. 古代日本の基本法典である「大宝律令」が701年に制定され, 古代日本の法的整備がなされました. 中国では唐の時代, 日本では律令国家の制度を取り入れた頃から, 式部省大学寮 (官吏養成機関)の算法教育の教科書として, 「孫子算経」が使われていました.
剰余計算は, 7世紀のインド, 18世紀以降のヨーロッパ, 江戸時代の和算においても かなり研究されていました. 例えば, 古代インドの数学者はブラマグプタ (Brahmagupta, 598-?) は ブラマの正当システム(Brahma-Sphuta-Siddhanta, Brahma’s Correct System) と呼ばれる次の問題を述べております.
「市場にきた老女の卵を入れたかごを馬が踏み潰しました. 馬の持ち主は老女に潰された卵を弁償することを申し入れました. 老女はかごに入れた卵の個数を正確に覚えていなかったのですが, 2個ずつ分けても, 3個ずつ分けても, 4個ずつ分けても, 5個ずつ分けても, 6個ずつ分けても1個余るが, 7個ずつ分けると余りがないことを覚えていました. かごの中の卵の可能な数の最小値はいくらですか?」
有理数係数の1変数の代数方程式のうち, 1次方程式, ax + b= 0 の解法は自明です. 2次方程式, ax2 + bx + c=0の解法は, 628年頃にインドの数学者, プラマグプタによって示されました. 9世紀にバグダッドあたりで活躍したアラビア人数学者, アル・フワリズム (Al Khawarizmi, 780-850頃) の著した算術書, 「インドの数の計算法」 (そのラテン語訳の題名は, ”Algorithmi de Numbers Indorum”)によって, 2次方程式の解法はヨーロッパに伝わりました. この書は825年に著され, 加減乗除の算法, 2次方程式の解法, 幾何学, 零の記号を 用いた10進記数法などを取り扱っています. アラビアで発達した代数学は, 方程式の解を求めることが重要なテーマでした. 2次方程式の解法で見られるように, 整数, 分数と共に, 平方根などの根数も 数として取り扱うようになりました. 中世ヨーロッパの大学では, アル・フワリズムの算術書は数学の主要な教科書として 500年にわたって用いられていました. 3次方程式や4次方程式の解法は16世紀にイタリアの数学者達によって示されました. アル・フワリズムの「算術書」は中世以降のヨーロッパにおいて, 代数方程式の解法の研究が盛んに行われ, 近代代数学に発展していった源流でした. アルジェブラやアルゴリズムという語はこの算術書に由来します.
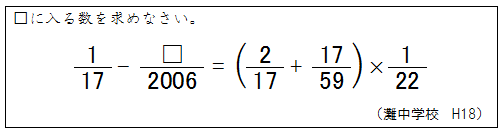
例年、1月から2月かけて行われる中学入試。最近はその時期になると、いわゆる”有名進学校”の難問がネットでも話題になるようです。
さすが有名な学校は違うな、という率直に感嘆する声がある一方で、こんな難しい問題を小学生に解かせるなんて、という批判の声もあります。小学生に難しい問題を解かせることに賛否両論はあっていいと思いますが、しかし、こういった学校は別に小学生をいじめたくて難しい問題を出題するわけではありません。
中学受験に詳しくない人にも名前を知られているような学校はいくつかありますが、特にそういう学校は、どういう生徒に来て欲しいか、という明確なイメージがあります。そして、そういう子たちが、というより、そういう子たちだけが解けるような問題を出しているのです。
たとえば、私の母校でもある灘中学校は、日本一中学入試の算数が難しい学校です。この学校の入試は2日にわけて行われますが、算数も、1日目と2日目の両方にそれぞれあります。そして、1日目は13題前後の1問1答式、2日目は逆に大問5問の記述式、というまったく毛色の違う2種類の算数のテストを受験生に課すのです。
この灘中学校が生徒として欲しがっている人材は明確で、言ってみれば”理系のエキスパート“です。1日目では、短時間で勘所を見抜くセンスを問われ、2日目はじっくり丁寧に考える思考力や遂行力が問われます。要するにこの学校は、センスもあって、粘り強い思考もできる子どもがほしいです、なんて贅沢なことを堂々と宣言しているわけです。(しかし、それこそ日本全国からそういう子どもたちが集まってくるので、そうそう無茶な要求でもなかったりするのが恐ろしいところです。かく言う私も、その”最強”感に憧れて灘中を目指した一人ですが。)
中学校がなぜそういう子どもたちを求めるか、というと、もちろん進学実績を出すため、ということもあるでしょう。しかしそれより、入学後のカリキュラムの問題も大きいです。
これは灘中学に限った話ではありませんが、いわゆる有名進学校では、中学1年生の間に中学内容の数学を終わらせてしまう、と言われています(実際には中2の頭くらいまでかかりますが)。
それじゃあ、中学校の間に高校までの範囲が終わっちゃうんじゃないの、後は何をするの?と思うかもしれません。しかしこれは少し予想と違って、実際には高校の範囲の学習を4年かけておこないます。つまり、中学内容を駆け足で終らせ、それによって、高校内容をじっくり学習するための時間の余裕を作るのです。
中学くらいまではなんとかついていっていたけど、高校に入ったら数学がわからなくなった、という人も多いと思います。それは言ってみれば当然の話で、高校内容の数学はそもそもとても難しいです。個人的には、3年間学校で習ったくらいで理解できるものではないと思っています。だからこそ、進学校では可能な限り多くの時間をその学習のために確保したいですし、そのために中学内容を手早く終わらせてしまいたいのです。そして、そういうカリキュラムを組むために、中学内容の数学くらいまでは、すでにある程度身につけている子どもがほしいのです。
もちろん、だからといって、単に”中学内容を先取りしている子ども”がほしいわけではありません。
冒頭の”計算問題”を見て下さい。「=(イコール)」の左側だけでなく、右側にも式があります。この形は何を意識しているかというと、「方程式」を想定しているわけです。
つまり、方程式の解ける子どもがほしい、と言っても、単純に「x」や「y」が使えるかどうかではなく、「複雑な方程式を解ききる技術」を実際に持っているかどうか、を見ているのです。(ちなみに、冒頭の問題は、灘中学校の1日目の1番目のもので、例年こういった計算問題が出題されます。計算問題なので時間をかければ解くことはできますが、あまり時間をかけると他の問題に響くため、手早く正確に解くことが求められています。答えは81です。)
中学入試で数学ができるかどうかを見ている、ということは、中学入試の問題には数学の基礎的な部分のエッセンスが詰まっている、ということでもあります。そういった意味では、数学を学習する上で、中学入試の問題を解く、というのは、ひとつ重要な過程だと思います。もちろん、すべての子どもが中学受験をする必要はないでしょう。12歳の時点でそれができる子どもばかりだとも思いません。しかし、どこかの段階で中学入試の問題にふれておくことは、数学を受け入れる下地を作るためのいいトレーニングになると思うのです。
いつの間にか数学についていけなくなった人や、これから数学を学びなおしてみたい人は、まず中学入試の問題に挑戦してみるのもいいかもしれません。