算額（その821）

算額（その821）

宮城県栗原市瀬峰泉谷 瀬峰泉谷熊野神社奉納算額
徳竹亜紀子，谷垣美保，萬伸介：瀬峰泉谷熊野神社奉納算額をめぐる諸問題，仙台高等専門学校名取キャンパス 研究紀要 第60号(2024)
https://www.sendai-nct.ac.jp/natori-library/wp/wp-content/uploads/2024/03/kiyo2024-1.pdf

外円内に円弧，甲円，乙円を入れる。円弧は外円と同じ半径で周長は外円の 1/3 である。乙円の直径が 3 寸のとき，甲円の直径はいかほどか。

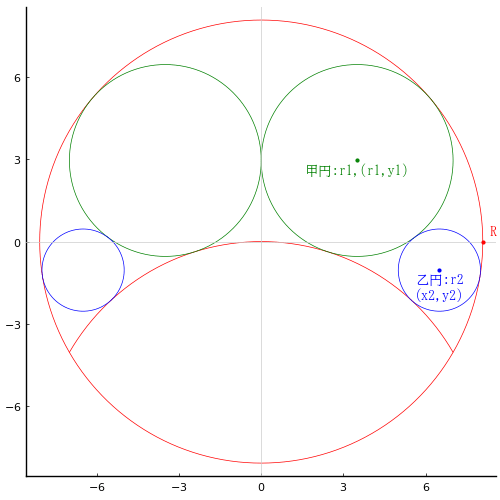
円弧は外円の中心を通る。
外円の半径と中心座標を R, (0, 0)
甲円の半径と中心座標を r1, (r1, y1)
乙円の半径と中心座標を r2, (x2, y2)
とおき，以下の連立方程式を解く。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy

@syms R::positive, r1::positive, y1::positive,
     r2::positive, x2::positive, y2::negative
#r2 = 3
eq1 = r1^2 + (y1 + R)^2 - (r1 + R)^2
eq2 = x2^2 + (R + y2)^2 - (r2 + R)^2
eq3 = (x2 - r1)^2 + (y1 - y2)^2 - (r1 + r2)^2
eq4 = r1^2 + y1^2 - (R - r1)^2
eq5 = x2^2 + y2^2 - (R - r2)^2;
res = solve([eq1, eq2, eq3, eq4, eq5], (R, r1, y1, x2, y2));
res[2]

   (4*r2*(109282*sqrt(2107560*sqrt(3) + 3650401) + 63094*sqrt(6322680*sqrt(3) + 10951203) + 319330453 + 184365523*sqrt(3))/(3*(14764*sqrt(3)*sqrt(2107560*sqrt(3) + 3650401) + 25572*sqrt(2107560*sqrt(3) + 3650401) + 47909161*sqrt(3) + 82981101)), r2*(258564*sqrt(2107560*sqrt(3) + 3650401) + 149282*sqrt(6322680*sqrt(3) + 10951203) + 755543964 + 436213511*sqrt(3))/(3*(34932*sqrt(2107560*sqrt(3) + 3650401) + 20168*sqrt(3)*sqrt(2107560*sqrt(3) + 3650401) + 113354292 + 65445131*sqrt(3))), 4*r2*(23094*sqrt(6322680*sqrt(3) + 10951203) + 40000*sqrt(2107560*sqrt(3) + 3650401) + 67482465*sqrt(3) + 116883058)/(3*(14764*sqrt(3)*sqrt(2107560*sqrt(3) + 3650401) + 25572*sqrt(2107560*sqrt(3) + 3650401) + 47909161*sqrt(3) + 82981101)), -260*sqrt(3)*r2*sqrt(62400*sqrt(3)*sqrt(2107560*sqrt(3) + 3650401) + 108080*sqrt(2107560*sqrt(3) + 3650401) + 187572840*sqrt(3) + 324885689) + 1351*r2*sqrt(62400*sqrt(3)*sqrt(2107560*sqrt(3) + 3650401) + 108080*sqrt(2107560*sqrt(3) + 3650401) + 187572840*sqrt(3) + 324885689)/3, -5404*r2*sqrt(6322680*sqrt(3) + 10951203)/9 - 10*sqrt(3)*r2/9 + 2*r2 + 1040*sqrt(3)*r2*sqrt(6322680*sqrt(3) + 10951203)/3)

2 組の解が得られるが，2 番目のものが適解である。

桁数の多い数値を含む複雑な式が得られるが，簡約化すると非常に単純な解になる。
R, r1, y1, x2, y2 の結果は以下のようになる。

res[2][1] |> sympy.sqrtdenest |> simplify |> println
res[2][2] |> sympy.sqrtdenest |> simplify |> println
res[2][3] |> sympy.sqrtdenest |> simplify |> println
res[2][4] |> sympy.sqrtdenest |> simplify |> println
res[2][5] |> sympy.sqrtdenest |> simplify |> println

   28*sqrt(3)*r2/9
   7*r2/3
   -14*sqrt(3)*r2/9 + 14*r2/3
   13*r2/3
   2*r2*(9 - 7*sqrt(3))/9

甲円の半径 r1 は乙円の半径 r2 の 7/3 倍である。
乙円の直径が 3 寸のとき，甲円の直径は 7 寸である。

2res[2][2](r2 => 3/2).evalf() |> println

   7.00000000000000

その他のパラメータは以下のとおりである。

R = 8.0829;  r1 = 3.5;  y1 = 2.95855;  x2 = 6.5;  y2 = -1.04145

function draw(more)
    pyplot(size=(500, 500), grid=false, showaxis=true, aspectratio=1, label="", fontfamily="IPAMincho")
   r2 = 3//2
   (R, r1, y1, x2, y2) = r2 .* (
       28√3/9,
       7/3,
       (42 - 14√3)/9,
       13/3,
       (18 - 14√3)/9)
   @printf("甲円の直径 = %g\n", 2r1)
   @printf("R = %g;  r1 = %g;  y1 = %g;  x2 = %g;  y2 = %g\n", R, r1, y1, x2, y2)
   plot()
   circle(0, 0, R)
   circle(0, -R, R, beginangle=30, endangle=150)
   circle2(r1, y1, r1, :green)
   circle2(x2, y2, r2, :blue)
   if more == true
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(r1, y1, "甲円:r1,(r1,y1)", :green, :center, delta=-delta/2)
       point(x2, y2, "乙円:r2\n(x2,y2)", :blue, :center, delta=-delta/2)
       point(R, 0, " R", :red, :left, :bottom, delta=delta/2)
   end
end;