算額（その1096）

算額（その1096）

五十八 岩手県花泉町 花泉天満宮 明治3年(1870)
山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市.
http://www.wasan.jp/yamamura/yamamura.html
キーワード：円5個，二等辺三角形

二等辺三角形の頂点を周上に持つ甲円と，二等辺三角形の中に乙円，丁円，丙円を容れる。乙円と丁円の直径がそれぞれ 15 寸，10 寸のとき，丙円の直径はいかほどか。

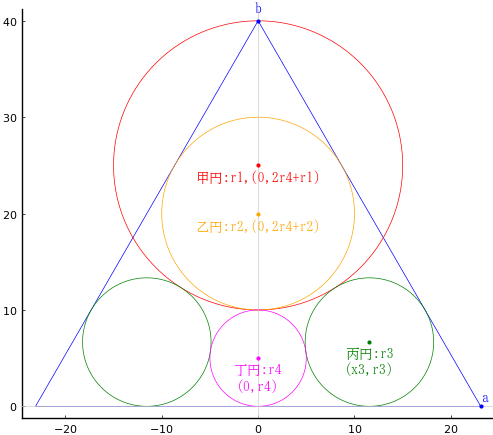
注：山村（算額も？）の図では丙円と甲円が離れているように描かれているが，それでは解は不定である。また，「答」にあるように丙円の直径が 16 寸のときには，算額のような図にはならない。算額に似るように描いた下図は甲円，丁円の直径が 10 寸，5 寸のときのものである。

二等辺三角形の底辺の長さを 2a，高さを b
甲円の半径と中心座標を r1, (0, 2r4 + r1)
乙円の半径と中心座標を r2, (0, 2r4 + r2)
丙円の半径と中心座標を r3, (x3, r3)
丁円の半径と中心座標を r4, (0, r4)
とおき，以下の連立方程式を解く。

include("julia-source.txt")

using SymPy

@syms a::positive, b::positive, r1::positive, r2::positive,
     r3::positive, x3::positive, r4::positive
eq1 = b - 2r1 - 2r4
#eq2 = r2/(b - r2 - 2r4) - a/sqrt(a^2 + b^2)
eq3 = dist2(0, b, a, 0, x3, r3, r3)
eq4 = dist2(0, b, a, 0, 0, 2r4 + r2, r2)
eq5 = x3^2 + (r4 - r3)^2 - (r3 + r4)^2 |> expand
eq6 = x3^2 + (2r4 + r1 - r3)^2 - (r1 + r3)^2 |> expand;
#res = solve([eq1, eq3, eq4, eq5, eq6], (a, b, r1, r3, x3))

println(eq1, ",  # eq1")
#println(eq2, ",  # eq2")
println(eq3, ",  # eq3")
println(eq4, ",  # eq4")
println(eq5, ",  # eq5")
println(eq6, ",  # eq6")

   b - 2*r1 - 2*r4,  # eq1
   b*(a^2*b - 2*a^2*r3 - 2*a*b*x3 + 2*a*r3*x3 - b*r3^2 + b*x3^2),  # eq3
   a^2*b^2 - 2*a^2*b*r2 - 4*a^2*b*r4 + 4*a^2*r2*r4 + 4*a^2*r4^2 - b^2*r2^2,  # eq4
   -4*r3*r4 + x3^2,  # eq5
   -4*r1*r3 + 4*r1*r4 - 4*r3*r4 + 4*r4^2 + x3^2,  # eq6

eq1, eq5 をそれぞれ解いて，r1, r3 を求める。

ans_r1 = solve(eq1, r1)[1]
ans_r1 |> println

   b/2 - r4

ans_r3 = solve(eq5, r3)[1]
ans_r3 |> println

   x3^2/(4*r4)

eq3, eq4, eq6 に r1, r3 を代入し整理する。

eq3 = eq3(r1 => ans_r1, r3 => ans_r3) |> simplify |> (x -> x*16r4^2/b)
eq4 = eq4(r1 => ans_r1, r3 => ans_r3)
eq6 = eq6(r1 => ans_r1, r3 => ans_r3)*2r4 |> simplify;

eq6 を解いて b を求める。

ans_b = solve(eq6, b)[1] |> simplify
ans_b |> println

   2*r4*x3^2/(-4*r4^2 + x3^2)

eq3, eq4 に b を代入し整理する。

eq3 = eq3(b => ans_b) |> simplify |> (x -> x*(4r4^2 - x3^2)) |> expand |> simplify |> (x -> x/(2r4*x3^2))
eq4 = eq4(b => ans_b) |> simplify |> numerator |> (x -> x/4r4^2);

eq3, eq4 を解いて，a, x3 を求める。

res = solve([eq3, eq4], (a, x3))[4]
res[1] |> println

   4*r2*r4^(3/2)*sqrt(r2 + r4)*(3*r2^16 + 44*r2^15*r4 + 300*r2^14*r4^2 + 1260*r2^13*r4^3 + 3640*r2^12*r4^4 + 7644*r2^11*r4^5 + 12012*r2^10*r4^6 + 14300*r2^9*r4^7 + 12870*r2^8*r4^8 + 8580*r2^7*r4^9 + 4004*r2^6*r4^10 + 1092*r2^5*r4^11 - 140*r2^3*r4^13 - 60*r2^2*r4^14 - 12*r2*r4^15 - r4^16)/(3*r2^18 + 44*r2^17*r4 + 297*r2^16*r4^2 + 1216*r2^15*r4^3 + 3340*r2^14*r4^4 + 6384*r2^13*r4^5 + 8372*r2^12*r4^6 + 6656*r2^11*r4^7 + 858*r2^10*r4^8 - 5720*r2^9*r4^9 - 8866*r2^8*r4^10 - 7488*r2^7*r4^11 - 4004*r2^6*r4^12 - 1232*r2^5*r4^13 - 60*r2^4*r4^14 + 128*r2^3*r4^15 + 59*r2^2*r4^16 + 12*r2*r4^17 + r4^18)

res[2] |> println

   4*r4^(3/2)/sqrt(r2 + r4)

a はかなり複雑な分数式であるが，分子，分母を別々に簡約化して再度分数式にすることで，簡約化できる。

num = res[1] |> numerator |> factor
den = res[1] |> denominator |> factor;

ans_a = num/den
ans_a |> println

   4*r2*r4^(3/2)/((r2 - r4)*sqrt(r2 + r4))

二等辺三角形の底辺の長さの半分 a は 4*r2*r4^(3/2)/((r2 - r4)*sqrt(r2 + r4)) により計算できる。
r2 =7.5, r4 = 5 のとき，a = 37.9473319220205 である。

ans_a(r2 => 7.5, r4 => 5).evalf() |> println

   37.9473319220205

x3 は 4*r4^(3/2)/sqrt(r2 + r4) により計算できる。
r2 =7.5, r4 = 5 のとき，x3 = 12.6491106406735 である。

res[2](r2 => 7.5, r4 => 5).evalf() |> println

   12.6491106406735

a, x3 が求まった後，b, r1, r3 は逆にたどって以下のようにして求める。

r2 = 7.5
r4 = 5
a = 4*r2*r4^(3/2)/((r2 - r4)*sqrt(r2 + r4))
x3 = 4*r4^(3/2)/sqrt(r2 + r4)
b = 2*r4*x3^2/(-4*r4^2 + x3^2)
r1 = b/2 - r4
r3 = x3^2/(4*r4)
(a, b, r1, r3, x3) |> println

   (37.94733192202055, 26.666666666666657, 8.333333333333329, 8.000000000000002, 12.649110640673518)

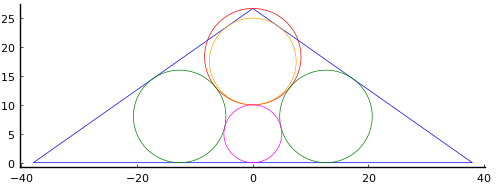
乙円，丁円の直径が 15 寸，10 寸のとき，丙円の直径は 16 寸である。　
以下のような図になる。

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (r2, r4) = (15, 10)./2
   r2 = 10
   r4 = 5
   a = 4*r2*r4^(3/2)/((r2 - r4)*sqrt(r2 + r4))
   x3 = 4*r4^(3/2)/sqrt(r2 + r4)
   b = 2*r4*x3^2/(-4*r4^2 + x3^2)
   r1 = b/2 - r4
   r3 = x3^2/(4*r4)
   @printf("乙円，丁円の直径が %g, %g のとき，丙円の直径は %g である。\n", 2r2, 2r4, 2r3)
   plot([a, 0, -a, a], [0, b, 0, 0], color=:blue, lw=0.5)
   circle(0, 2r4 + r1, r1)
   circle(0, 2r4 + r2, r2, :orange)
   circle2(x3, r3, r3, :green)
   circle(0, r4, r4, :magenta)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(0, 2r4 + r1, "甲円:r1,(0,2r4+r1)", :red, :center, delta=-delta)
       point(0, 2r4 + r2, "乙円:r2,(0,2r4+r2)", :orange, :center, delta=-delta)
       point(x3, r3, "丙円:r3\n(x3,r3)", :green, :center, delta=-delta)
       point(0, r4, "丁円:r4\n(0,r4)", :magenta, :center, delta=-delta)
       point(a, 0, "a", :blue, :left, :bottom, delta=delta/2)
       point(0, b, "b", :blue, :center, :bottom, delta=delta)
   end
end;