算額(その472)
宮城県角田市横倉 愛宕神社 明治15年(1882)1月
http://www.wasan.jp/miyagi/yokokuraatago.html
徳竹亜紀子,谷垣美保: 2021年度の算額調査,仙台高等専門学校名取キャンパス 研究紀要,第 58 号, p.7-28, 2022.
https://www.sendai-nct.ac.jp/natori-library/wp/wp-content/uploads/2022/03/kiyo2022-2.pdf
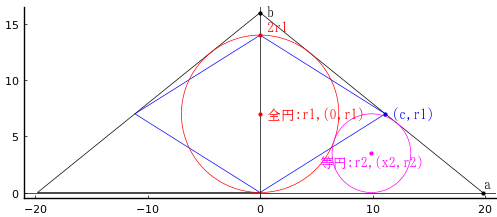
団扇の中に,正三角形,大円 2 個,小円 2 個が入っている。大円の直径が 23 寸 4 分のとき,小円の直径はいかほどか。

扇を構成する外円の半径と中心座標を r0, (0, 0)
大円の半径と中心座標を r1, (r1, r1 - r0/2)
小円の半径と中心座標を r2, (x2, -r2 - r0/2)
団扇の下部の円弧の半径と中心座標を r0/2, (0, -r0)
外円と円弧の交点座標を (x, y)
とおき,以下の連立方程式を解く。
include("julia-source.txt")
using SymPy
@syms r0::positive, r1::positive, r2::positive, x2::positive;
r1 = 234//20
eq1 = x2^2 + (r0/2 - r2)^2 - (r0/2 + r2)^2
eq2 = r1^2 + (r1 - r0/2)^2 - (r0 - r1)^2
eq3 = x2^2 + (-r0/2 - r2)^2 - (r0 - r2)^2
res = solve([eq1, eq2, eq3], (r0, r2, x2))
1-element Vector{Tuple{Sym, Sym, Sym}}:
(117/5, 351/100, 117*sqrt(30)/50)
外円の直径は大円の直径の 2 倍である(方程式によらなくてもわかることではあるが)。
小円の直径は大円の直径の 3/10 倍である。23.4*3/10 = 7.02 = 7寸0分2厘である。
術では「大円の直径を3倍して「1位ずらす」(10で割る)」ことで,7 寸としている(普通は 7 寸あまりありと記載される)。
図を描くために円弧の描き始めと描き終わりの角度を求めるために,外円と円弧の交点座標 (x, y) を求める。
using SymPy
@syms r0::positive, r1::positive, x, y;
r1 = 234//20
r0 = 117//5
eq11 = x^2 + y^2 - r0^2
eq12 = x^2 + (y + r0)^2 - (r0/2)^2
rs2 = solve([eq11, eq12], (x, y))
2-element Vector{Tuple{Sym, Sym}}:
(-117*sqrt(15)/40, -819/40)
(117*sqrt(15)/40, -819/40)
using Plots
function draw(more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
r1 = 234//20
(r0, r2, x2) = (2*r1, 3*r1/10, sqrt(30)*r1/5)
@printf("小円の直径 = %g; r0 = %g; r1 = %g; r2= %g; x2= %g\n", 2r2, r0, r1, r2, x2)
plot([√3r0/2, 0, -√3r0/2, √3r0/2], [-r0/2, r0, -r0/2, -r0/2], color=:black, lw=0.5)
circle(0, 0, r0, :black)
circle(r1, r1 - r0/2, r1, :red)
circle(-r1, r1 - r0/2, r1, :red)
circle(x2, -r2 - r0/2, r2, :blue)
circle(-x2, -r2 - r0/2, r2, :blue)
(x, y) = (117*sqrt(15)/40, -819/40)
θ = round(Int, atand(Float64((y + r0)/x)))
circle(0, -r0, r0/2, :green, beginangle=θ, endangle=180 - θ)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) / 3 # size[2] * fontsize * 2
hline!([0], color=:black, lw=0.5)
vline!([0], color=:black, lw=0.5)
point(r1, r1 - r0/2, "大円:r1,(r1,r1-r0/2)", :red, :center, :top, delta=-delta)
point(x2, -r2 - r0/2, "小円:r2,(x2,-r2-r0/2)", :blue, :center, :top, delta=-delta)
point(0, -r0/2, " -r0/2", :black, :left, :bottom, delta=delta/3)
point(0, -r0, " -r0", :green, :left, :bottom, delta=delta/3)
point(√3r0/2, -r0/2, "(√3r0/2,-r0/2) ", :black, :right, :bottom, delta=delta/3)
point(x, y, "(x,y)")
end
end;