算額（その453）

算額（その453）

(17) 兵庫県姫路市飾磨区英賀宮町 英賀神社 明治12年(1879)
近畿数学史学会：近畿の算額「数学の絵馬を訪ねて」，平成4年5月16日 初版第一刷，大阪教育図書株式会社，大阪市.

森田健(2020): 日本文化としての数学：和算と算額, 日本語・日本文化，2020，47，p81-107.
https://ir.library.osaka-u.ac.jp/repo/ouka/all/75881/JLC_47_081.pdf

キーワード：円3個，直角三角形

鈎股弦の中に大円，中円，小円が入っている。鈎が 30 寸，股が 40 寸のとき，中円の直径を求めよ。

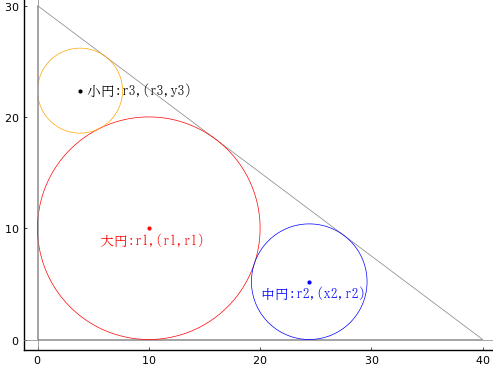
大円の半径と中心座標を r1, (r1, r1)
中円の半径と中心座標を r2, (x2, r2)
小円の半径と中心座標を r3, (x3, y3)
とし，以下の連立方程式を解く。

与えられた条件（鈎が 30 寸，股が 40 寸）のとき，弦が 50 寸であることはすぐに分かるが，一応連立方程式の中にはいれておく。

include("julia-source.txt")

using SymPy

@syms r1::positive, r2::positive, x2::positive, r3::positive, y3::positive,
     鈎::positive, 股::positive, 弦::positive;

eq1 = (r1 - r3)^2 + (y3 - r1)^2 - (r1 + r3)^2
eq2 = (x2 - r1)^2 + (r1 - r2)^2 - (r1 + r2)^2
eq3 = 鈎 + 股 - 弦 - 2r1
eq4 = (股 + 弦)r2 + x2*鈎 - 鈎*股
eq5 = (鈎 + 股 + 弦)r1 - 鈎*股
eq6 = (鈎 + 弦)r3 + y3*股 - 鈎*股
res = solve([eq1, eq2, eq3, eq4, eq5, eq6], (r1, r2, x2, r3, y3, 弦));

4 組の解が得られるが，4 番目のものが適解である。
それぞれの解は，かなり長い式である。
鈎 = 30, 股 = 40 の場合は，各変数は以下のような値になる。

names = ("r1", "r2", "x2", "r3", "y3", "弦")
i = 4
for (j, name) = enumerate(names)
   @printf("%2s = %g\n", name, res[i][j](鈎 => 30, 股 => 40).evalf())
end

   r1 = 10
   r2 = 5.19494
   x2 = 24.4152
   r3 = 3.81966
   y3 = 22.3607
   弦 = 50

中円の半径は 2(110 - 20√10)/9 = 10.3898770659183 である。

算額の答えでは「10寸」となっているが，「約 10 寸」ということである。

2res[4][2](鈎 => 30, 股 => 40) |> simplify |> println
2res[4][2](鈎 => 30, 股 => 40).evalf() |> println

   220/9 - 40*sqrt(10)/9
   10.3898770659183

なお，小円の存在はダミーである。これがなくても中円の半径を求める方程式群で解が得られる（2 組のうちの 2 番目のもの）。

res2 = solve([eq2, eq3, eq4, eq5], (r1, r2, x2, 弦));
2res2[2][2](鈎 => 30, 股 => 40) |> println
2res2[2][2](鈎 => 30, 股 => 40).evalf() |> println

   220/9 - 40*sqrt(10)/9
   10.3898770659183

using Plots

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (鈎, 股) = (30, 40)
   (r1, r2, x2, r3, y3, 弦) = (股/2 + 鈎/2 - sqrt(股^2 + 鈎^2)/2, (8*股^3 + 4*股^2*鈎 - 8*股^2*sqrt(股^2 + 鈎^2) + 7*股*鈎^2 - 4*股*鈎*sqrt(股^2 + 鈎^2) + 4*股*sqrt(2*股^4 + 2*股^3*鈎 - 2*股^3*sqrt(股^2 + 鈎^2) + 3*股^2*鈎^2 - 2*股^2*鈎*sqrt(股^2 + 鈎^2) + 2*股*鈎^3 - 2*股*鈎^2*sqrt(股^2 + 鈎^2) + 鈎^4 - 鈎^3*sqrt(股^2 + 鈎^2)) + 3*鈎^3 - 3*鈎^2*sqrt(股^2 + 鈎^2) - 4*sqrt(2*股^6 + 2*股^5*鈎 - 2*股^5*sqrt(股^2 + 鈎^2) + 5*股^4*鈎^2 - 2*股^4*鈎*sqrt(股^2 + 鈎^2) + 4*股^3*鈎^3 - 4*股^3*鈎^2*sqrt(股^2 + 鈎^2) + 4*股^2*鈎^4 - 3*股^2*鈎^3*sqrt(股^2 + 鈎^2) + 2*股*鈎^5 - 2*股*鈎^4*sqrt(股^2 + 鈎^2) + 鈎^6 - 鈎^5*sqrt(股^2 + 鈎^2)))/(2*鈎^2), (4*股^2 + 3*股*鈎 - 4*股*sqrt(股^2 + 鈎^2) + 3*鈎^2 - 3*鈎*sqrt(股^2 + 鈎^2) + 4*sqrt(2*股^4 + 2*股^3*鈎 - 2*股^3*sqrt(股^2 + 鈎^2) + 3*股^2*鈎^2 - 2*股^2*鈎*sqrt(股^2 + 鈎^2) + 2*股*鈎^3 - 2*股*鈎^2*sqrt(股^2 + 鈎^2) + 鈎^4 - 鈎^3*sqrt(股^2 + 鈎^2)))/(2*鈎), (3*股^3 + 7*股^2*鈎 - 3*股^2*sqrt(股^2 + 鈎^2) + 4*股*鈎^2 - 4*股*鈎*sqrt(股^2 + 鈎^2) + 8*鈎^3 - 8*鈎^2*sqrt(股^2 + 鈎^2) + 4*鈎*sqrt(股^4 + 2*股^3*鈎 - 股^3*sqrt(股^2 + 鈎^2) + 3*股^2*鈎^2 - 2*股^2*鈎*sqrt(股^2 + 鈎^2) + 2*股*鈎^3 - 2*股*鈎^2*sqrt(股^2 + 鈎^2) + 2*鈎^4 - 2*鈎^3*sqrt(股^2 + 鈎^2)) - 4*sqrt(股^6 + 2*股^5*鈎 - 股^5*sqrt(股^2 + 鈎^2) + 4*股^4*鈎^2 - 2*股^4*鈎*sqrt(股^2 + 鈎^2) + 4*股^3*鈎^3 - 3*股^3*鈎^2*sqrt(股^2 + 鈎^2) + 5*股^2*鈎^4 - 4*股^2*鈎^3*sqrt(股^2 + 鈎^2) + 2*股*鈎^5 - 2*股*鈎^4*sqrt(股^2 + 鈎^2) + 2*鈎^6 - 2*鈎^5*sqrt(股^2 + 鈎^2)))/(2*股^2), (3*股^2 + 3*股*鈎 - 3*股*sqrt(股^2 + 鈎^2) + 4*鈎^2 - 4*鈎*sqrt(股^2 + 鈎^2) + 4*sqrt(股^4 + 2*股^3*鈎 - 股^3*sqrt(股^2 + 鈎^2) + 3*股^2*鈎^2 - 2*股^2*鈎*sqrt(股^2 + 鈎^2) + 2*股*鈎^3 - 2*股*鈎^2*sqrt(股^2 + 鈎^2) + 2*鈎^4 - 2*鈎^3*sqrt(股^2 + 鈎^2)))/(2*股), sqrt(股^2 + 鈎^2))
   @printf("中円の直径 = %g\n", 2r2)
   plot([0, 股, 0, 0], [0, 0, 鈎, 0], color=:gray, lw=0.5)
   circle(r1, r1, r1, :red)
   circle(x2, r2, r2, :blue)
   circle(r3, y3, r3, :orange)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /  3  # size[2] * fontsize * 2
       point(r1, r1, " 大円:r1,(r1,r1)", :red, :center, :top, delta=-delta)
       point(x2, r2, " 中円:r2,(x2,r2)", :blue, :center, :top, delta=-delta)
       point(r3, y3, " 小円:r3,(r3,y3)", :black, :left, :vcenter)
       hline!([0], color=:gray, lw=0.5)
       vline!([0], color=:gray, lw=0.5)
   else
      plot!(showaxis=false)
   end
end;

算額（その452）

算額（その452）

群馬県高崎市白岩町 長谷寺（白岩観音） 文久元年(1861)

森田健(2020): 日本文化としての数学：和算と算額, 日本語・日本文化，2020，47，p81-107.
https://ir.library.osaka-u.ac.jp/repo/ouka/all/75881/JLC_47_081.pdf

正方形の中に，大円 2 個，中円 3 個，小円2 個が図のように配置されている。正方形の一辺の長さがわかっているとき，小円の直径を求めよ。

正方形の一辺の長さを a とする。
大円の半径と中心座標を r1, (r2, 0)
中円の半径と中心座標を r2, (0, 0), (2r2, 0)
小円の半径と中心座標を r3, (0, a/2 - r3)
とし，以下の連立方程式を解く。

include("julia-source.txt")

using SymPy

@syms a::positive, r1::positive, r2::positive, r3::positive;
r2 = a/6
r1 = 2r2
eq1 = r2^2 + (a/2 - r3)^2 - (r1 + r3)^2
res = solve(eq1, r3)[1]
res |> println

   a/10

小円の半径は正方形の一辺の長さの 1/10 である。直径は 1/5 である。

using Plots

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   a = 1
   r2 = a/6
   r1 = 2r2
   r3 = a/10
   @printf("a = %g; r3 = %g\n", a, r3)
   @printf("小円の直径 = %g\n", 2r3)
   plot([a, a, -a, -a, a] ./ 2, [-a, a, a, -a, -a] ./ 2, color=:black, lw=0.5)
   circle(r2, 0, r1, :red)
   circle(-r2, 0, r1, :red)
   circle(0, 0, r2, :blue)
   circle(2r2, 0, r2, :blue)
   circle(-2r2, 0, r2, :blue)
   circle(0, a/2 - r3, r3, :orange)
   circle(0, r3 - a/2, r3, :orange)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /  3  # size[2] * fontsize * 2
       point(a/2, a/2, "(a/2,a/2)", :black, :right, :bottom, delta=delta/2)
       point(0, a/2 - r3, " 小円:r3,(0,a/2-r3)", :black, :left, :vcenter)
       point(r2, 0, " 大円:r1,(r2,0)", :red, :left, :bottom, delta=delta/2)
       point(2r2, 0, " 中円:r2,(2r2,0)", :blue, :center, :top, delta=-delta/2)
       hline!([0], color=:gray, lw=0.5)
       vline!([0], color=:gray, lw=0.5)
   else
      plot!(showaxis=false)
   end
end;